En mathématiques, une relation d'équivalence permet, dans un ensemble, de mettre en relation des éléments qui sont similaires par une certaine propriété. On pourra ainsi regrouper ces éléments par « paquets » d'éléments qui se ressemblent, définissant ainsi la notion de classe d'équivalence, pour enfin construire de nouveaux ensembles en « assimilant » les éléments similaires à un seul et même élément. On aboutit alors à la notion d'ensemble quotient.
Exemple intuitif
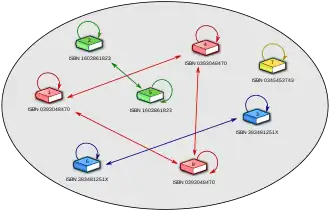
Considérons un ensemble de huit exemplaires de livres, comme le montre la figure à droite. Par exemple : deux exemplaires du même dictionnaire Le Robert (en bleu), deux exemplaires d'un même livre de botanique (en vert), trois exemplaires du même livre de mathématiques (en rouge), et un livre de sciences-fiction (en jaune). La relation « … a le même ISBN que … » est une relation d'équivalence. Par exemple, Deux exemplaires du même dictionnaire ont le même ISBN et sont donc "en relation". On peut regrouper ces exemplaires ensemble : un paquet avec les deux dictionnaires, un paquet avec les deux livres de botaniques, etc. Les paquets sont les classes d'équivalence. L'ensemble de ces quatre paquets est un ensemble quotient.
Comme on le verra dans la définition formelle qui suit, une relation d'équivalence est :
- réflexive : un exemplaire a le même ISBN que lui-même ;
- symétrique : si un exemplaire A a le même ISBN que l'exemplaire B alors l'exemplaire B a aussi le même ISBN que A ;
- transitive : si un exemplaire A a le même ISBN que l'exemplaire B, qui a le même ISBN qu'un exemplaire C, alors l'exemplaire A a le même ISBN que l'exemplaire C.
Définition
Définition formelle
Une relation d'équivalence sur un ensemble E est une relation binaire ~ sur E qui est à la fois réflexive, symétrique et transitive.
Plus explicitement :
- ~ est une relation binaire sur E : un couple (x, y) d'éléments de E appartient au graphe de cette relation si et seulement si x ~ y.
- ~ est réflexive : pour tout élément x de E, on a x ~ x.
- ~ est symétrique : chaque fois que deux éléments x et y de E vérifient x ~ y, ils vérifient aussi y ~ x.
- ~ est transitive : chaque fois que trois éléments x, y et z de E vérifient x ~ y et y ~ z, ils vérifient aussi x ~ z.
Par réflexivité, E coïncide alors avec l'ensemble de définition de ~ (qui se déduit du graphe par projection). Inversement, pour qu'une relation binaire sur E symétrique et transitive soit réflexive, il suffit que son ensemble de définition soit E tout entier[1].
Définition équivalente
On peut aussi définir une relation d'équivalence comme une relation binaire réflexive et circulaire[2].
Une relation binaire ~ est dite circulaire si chaque fois qu'on a x ~ y et y ~ z, on a aussi z ~ x.
Classe d'équivalence
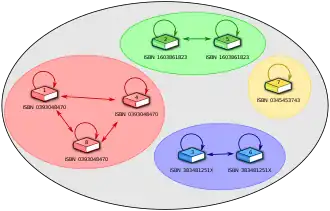
Fixons un ensemble E et une relation d'équivalence ~ sur E.
On définit la classe d'équivalence [x] d'un élément x de E comme l'ensemble des y de E tels que x ~ y :
On appelle représentant de [x] n'importe quel élément de [x], et système de représentants des classes toute partie de E qui contient exactement un représentant par classe[3].
- L'ensemble des classes d'équivalence forme une partition de E.
Inversement, toute partition d'un ensemble E définit une relation d'équivalence sur E. Ceci établit une bijection naturelle entre les partitions d'un ensemble et les relations d'équivalence sur cet ensemble. Le nombre de relations d'équivalence sur un ensemble à n éléments est donc égal au nombre de Bell Bn, qui peut se calculer par récurrence.
Exemples
- Le parallélisme, sur l'ensemble des droites d'un espace affine, est une relation d'équivalence, dont les classes sont les directions.
- Toute application f : E → F induit sur E la relation d'équivalence « avoir même image par f ».
- Lorsque cette application est injective, la relation d'équivalence qu'elle induit sur E est l'égalité, dont les classes sont les singletons.
- Sur l'ensemble ℤ des entiers relatifs, la congruence modulo n (pour un entier n fixé) est une relation d'équivalence, dont les classes forment le groupe cyclique ℤ/nℤ.
- Plus généralement, si G est un groupe et H un sous-groupe de G alors la relation ~ sur G définie par (x ~ y ⇔ y−1x ∈ H) est une relation d'équivalence, dont les classes sont appelées les classes à gauche suivant H.
- L'égalité presque partout, pour des fonctions sur un espace mesuré, est une relation d'équivalence qui joue un rôle important dans la théorie de l'intégration de Lebesgue. En effet, deux fonctions égales presque partout ont le même comportement dans cette théorie.
- On trouve d'autres exemples dans les articles suivants :
- Équipollence,
- Préordre,
- Action de groupe,
- Espace projectif,
- Matrices congruentes, Matrices équivalentes, Matrices semblables,
- Triangles isométriques, Triangles semblables,
- Construction des entiers relatifs, Corps des fractions, Complété d'un espace métrique,
- Topologie quotient,
- Équivalence d'homotopie,
- Germe.
- Contre-exemples
Beaucoup de relations sont réflexives, symétriques ou transitives, sans être les trois à la fois :
- un préordre est réflexif et transitif par définition, mais pas symétrique en général (exemple : un ordre sur une paire) ;
- une relation d'équivalence partielle (en) est symétrique et transitive par définition, mais pas réflexive en général (exemple trivial : sur un ensemble non vide, la relation de graphe vide) ;
- une relation de tolérance est réflexive et symétrique par définition, mais pas transitive en général (exemple : sur les entiers, la relation ~ définie par : m ~ n ⇔ |m – n| ≤ 1).
- Remarque
On peut munir une classe propre d'une relation d'équivalence. On peut même y définir des classes d'équivalence, mais elles peuvent être elles-mêmes des classes propres, et ne forment généralement pas un ensemble (exemple : la relation d'équipotence dans la classe des ensembles).
Ensemble quotient
On donne ce nom à la partition de E mise en évidence ci-dessus, qui est donc un sous-ensemble de l'ensemble des parties de E.
Définition
Étant donné une relation d'équivalence ~ sur E, l'ensemble quotient de E par la relation ~, noté E/~, est le sous-ensemble de des classes d'équivalence :
L'ensemble quotient peut aussi être appelé « l'ensemble E quotienté par ~ » ou « l'ensemble E considéré modulo ~ ». L'idée derrière ces appellations est de travailler dans l'ensemble quotient comme dans E, mais sans distinguer entre eux les éléments équivalents selon ~.
Surjection canonique
L'application canonique p, de E dans l'ensemble quotient, qui à chaque élément de E associe sa classe d'équivalence :
- est surjective par construction car est l'image de l'application de dans ;
- n'est en général pas injective (sauf si ~ est l'égalité), puisqu'on a seulement
Une telle application p est appelée une projection. Elle vérifie la propriété universelle suivante, qui exprime que toute application définie sur E dont la relation d'équivalence associée est moins fine que ~ « passe au quotient » E/~ de façon unique :
Théorème de factorisation — Pour toute application f : E → F vérifiant [x ~ y ⇒ f(x) = f(y)], il existe une unique application g : E/~ → F telle que f = g∘p.
Cette application g — qui a donc même image que f — est injective si et seulement si x ~ y ⇔ f(x) = f(y).
Structure quotient
Si E est muni d'une structure algébrique, il est possible de transférer cette dernière à l'ensemble quotient, sous réserve que la structure soit compatible (en) avec la relation d'équivalence, c'est-à-dire que deux éléments de E se comportent de la même manière vis-à-vis de la structure s'ils appartiennent à la même classe d'équivalence. L'ensemble quotient est alors muni de la structure quotient de la structure initiale par la relation d'équivalence.
Par exemple si ⊤ est une loi interne sur E compatible avec ~, c'est-à-dire vérifiant
(x ~ x' et y ~ y') ⇒ x⊤y ~ x'⊤y',
la « loi quotient de la loi ⊤ par ~ » est définie comme « la loi de composition sur l'ensemble quotient E/~ qui, aux classes d'équivalence de x et de y, fait correspondre la classe d'équivalence de x ⊤ y. »[4]
(Plus formellement : en notant p la surjection E × E → E/~ × E/~, (x, y) ↦ ([x], [y]) et f l'application E × E → E/~, (x, y) ↦ [x⊤y], l'hypothèse de compatibilité se réécrit p(x, y) = p(x', y') ⇒ f(x, y) = f(x', y'). En appliquant le théorème de factorisation ci-dessus, on peut donc définir la loi quotient comme l'unique application g : E/~ × E/~ → E/~ telle que f = g∘p.)
- Exemples
- Sur le corps ordonné des réels, la relation « a le même signe que » (comprise au sens strict) a trois classes d'équivalence :
- l'ensemble des entiers strictement positifs ;
- l'ensemble des entiers strictement négatifs ;
- le singleton {0}.
- La multiplication est compatible avec cette relation d'équivalence et la règle des signes est l'expression de la loi quotient.
- Si E est muni d'une structure de groupe, on associe à tout sous-groupe normal une relation d'équivalence compatible, ce qui permet de définir un groupe quotient.
- Sur le corps ordonné des réels, la relation « a le même signe que » (comprise au sens strict) a trois classes d'équivalence :
Relation d'équivalence engendrée
Sur un ensemble E, soit R une relation binaire, identifiée à son graphe. L'intersection de toutes les relations d'équivalence sur E qui contiennent R est appelée la relation d'équivalence (sur E) engendrée par R[5]. Elle est égale à la clôture réflexive transitive de R ∪ R−1.
Notes et références
- ↑ N. Bourbaki, Éléments de mathématique : Théorie des ensembles [détail des éditions], p. II-41 sur Google Livres.
- ↑ (en) W. D. Wallis, A Beginner's Guide to Discrete Mathematics, Springer Science+Business Media, , 2e éd. (DOI 10.1007/978-0-8176-8286-6, lire en ligne), p. 104.
- ↑ Bourbaki, Théorie des ensembles, p. II-42.
- ↑ N. Bourbaki, Éléments de mathématique, Algèbre, chapitres 1 à 3, p. I-11.
- ↑ Jean-Pierre Ramis, André Warusfel et al., Mathématiques. Tout-en-un pour la Licence. Niveau 1, Dunod, , 2e éd., 896 p. (ISBN 978-2-10-060013-7, lire en ligne), p. 31.
![y\in [x]\Leftrightarrow x\sim y.](https://img.franco.wiki/i/e077a02a4014be0be553d2ec99a0767a7876327d.svg)
![x\sim y\Leftrightarrow[x]=[y].](https://img.franco.wiki/i/285d3cf876b3cf3f3c2f53cc9c40e5e0027cb5ec.svg)

![{\displaystyle {E/\sim }~=~\{[x]\in {\mathcal {P}}(E)\mid x\in E\}.}](https://img.franco.wiki/i/d2b89041f959870f23111cc9731016993c625ac6.svg)
![\begin{matrix}p:&E&\rightarrow&{E/\sim}\\&x&\mapsto&[x]\end{matrix}](https://img.franco.wiki/i/c7dda6ccc378684b161d00ffb50265b9dadbcf38.svg)

![{\displaystyle x\mapsto [x]}](https://img.franco.wiki/i/a07b95c49afdb5a84f26120657148e94c94a69be.svg)

