| Naissance | Kashan |
|---|---|
| Décès | |
| Activités |
| A travaillé pour |
Observatoire astronomique d'Oulough Bek |
|---|
Al-Kashi ou Al-Kachi (« le natif de Kachan »), de son nom complet Ghiyath ad-Din Jamshid Mas`ud al-Kashi (Ghiyâth ad-dîn : « secours de la religion », mas`ûd : « heureux », ĵamšid : « Yama le brillant » en persan), est un mathématicien et astronome perse (v. 1380, Kachan (Territoire mozaffaride) – 1429, Samarcande (Empire timouride)).
Biographie
Dans les années qui suivirent une éclipse de lune à laquelle il assista en 1406 à Kachan, al-Kashi rédigea plusieurs ouvrages astronomiques. Ses Khaqani zij (Tables du grand khan) furent dédiées à Shah Rukh ou au fils de celui-ci, Ulugh Beg, sultans de la dynastie timouride.
Ulugh Beg invita al-Kashi à Samarcande en 1420, année de l'ouverture de la médersa qui porte son nom. Al-Kashi y enseigna avec Qadi-zadeh Roumi, le professeur d'Ulugh Beg, et probablement Ulugh Beg lui-même.
Contributions
Astronomie
Avant la construction de l'observatoire de Samarcande, les observations étaient réalisées à la médersa. Al-Kashi joua un rôle important dans la conception de l'observatoire, inauguré vers 1429, et de ses instruments d'astronomie.
Les travaux menés par Ulugh Beg, Qadi-zadeh Roumi, al-Kashi et quelque soixante autres savants aboutirent à la publication des Tables sultaniennes (Zij-é solTâni, en persan), parues en 1437 mais améliorées par Ulugh Beg jusque peu avant sa mort en 1449. Les données des Khaqani zij y furent bien sûr utilisées.
Des lettres écrites en persan par al-Kashi à son père décrivent en détail la vie scientifique à Samarcande à cette époque[1]. Seuls Qadi-zadeh Roumi et Ulugh Beg trouvent grâce à ses yeux. Al-Kashi était d'un tempérament peu raffiné, mais Ulugh Beg le traitait avec bienveillance du fait de ses compétences.
Mathématiques
Loi des cosinus
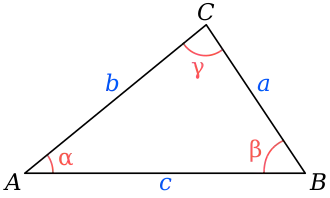
La loi des cosinus s'énonce de la façon suivante :
- Soit un triangle ABC, dans lequel on utilise les notations usuelles exposées sur la figure 1 : d'une part α, β et γ pour les angles et, d'autre part, a, b et c pour les longueurs des côtés respectivement opposés à ces angles. Alors l'égalité suivante est vérifiée :
Al-Kashi est crédité de l'énonciation de ce théorème dans son livre Miftah al-hisab (« Clé de l'arithmétique »).
Risala al-mouhitiyy (« Traité de la circonférence ») et calcul de π
En 1424, dans son ouvrage intitulé Risala al-mouhitiyy (« Traité de la circonférence »)[2], à partir de la méthode des polygones d'Archimède, en utilisant exclusivement la base 60 (sexagésimale)[2], al-Kashi calcule 10 chiffres sexagésimaux de π, soit 16 chiffres décimaux exacts[3]. Il publie ainsi le calcul suivant :
2π = 6 * 600 + 16 * 60−1 + 59 * 60−2 + 28 * 60−3 + 1 * 60-4 + 34 * 60-5 + 51 * 60-6 + 46 * 60-7 + 14 * 60-8 + 50 * 60-9,
ce qui donne, en décimal : π = 3,1415926535897932…
La valeur la plus précise obtenue jusque-là était celle du mathématicien chinois Zu Chongzhi (vers l'an 465) qui, par la méthode des périmètres, avait obtenu l'encadrement : 3,1415926 < π < 3,1415927.
Vers 1410, et de manière indépendante, le mathématicien indien Madhava avait déjà obtenu 11 décimales de π à l'aide d'une variante de la formule de Gregory.
Ce record sera battu 170 ans plus tard, en 1596, par l'Allemand van Ceulen, avec 20 décimales[4].
Miftah al-hisab (« Clé de l'arithmétique »)
Dans cette œuvre terminée en 1427, Al-Kashi utilise l'arithmétique pour résoudre des problèmes relevant de divers domaines tels que l'astronomie, la finance ou l'architecture[2].
Instruments
Al-Kashi est l'inventeur d'une sorte de calculateur analogique permettant de faire des interpolations linéaires, opérations très courantes en astronomie[5],[6],[7].
Œuvres (sélection)
- Jamshīd ibn Masʻūd Kāshī (auteur), Edward Stewart Kennedy (dir.) et Mary Helen Kennedy (dir.), Al-Kāshī's geographical table, vol. 77, partie 7, de Transactions of the American Philosophical Society, 1987 (ISBN 0871697785 et 9780871697783)
- Gamšīd Ġiyāṯ al-Dīn al-Kāšī (auteur), Aḥmad Saʿīd al-Damirdāš (dir.), Muḥammad Ḥamdī al-Ḥifnī al-Šayẖ (dir.), مفتاح الحساب (Miftāḥ al-ḥisāb), Le Caire, 1967 (Clé de l'arithmétique) — Ouvrage dédié à Oulough Beg[8]
Notes et références
- ↑ On peut lire en ligne un extrait d'une lettre d'Al-Kashi à son père, traduit par David A. King et Mary Helen Kennedy (dir.), Studies in the Islamic exact sciences. Reprints of papers by E. S. Kennedy, colleagues and former students, American University of Beirut, 1983, p. 724.
- 1 2 3 Yvonne Dold-Samplonius, « KĀSHĪ ou KACHI GHIYĀTH AL-DĪN JAMSHĪD MAS'ŪD AL- (mort en 1429) », sur Encyclopædia Universalis.
- ↑ « Al Kashi », sur L'univers de Pi.
- ↑ « Historique de Pi », sur TrucsMaths.
- ↑ (en) S. Frederick Starr, Lost Enlightenment : Central Asia's Golden Age from the Arab Conquest to Tamerlan, Princeton University Press, 2013, p. 495 (ISBN 1400848806 et 9781400848805).
- ↑ (en) Edward S. Kennedy, « Al-Kashi's "Plate of Conjunctions" », Isis, vol. 38, nos 1-2, , p. 56-59 (JSTOR 225450).
- ↑ (en) Edward S. Kennedy, « A Fifteenth-Century Planetary Computer: al-Kashi's "Tabaq al-Manateq" I. Motion of the Sun and Moon in Longitude », Isis, vol. 41, no 2, , p. 180-183 (JSTOR 227189).
- ↑ Lucien Kehren, « Ulugh Beg et l'École d'astronomie de Samarkand (XVe siècle) », dans Yves Vadé, Étoiles dans la nuit des temps, L'Harmattan, (lire en ligne).
Annexes
Bibliographie
- (en) Adolf P. Youschkevitch et Boris Rosenfeld, « Al-Kāshī », dans Complete Dictionary of Scientific Biography, vol. 7, Détroit, Charles Scribner's Sons, (ISBN 978-0-684-31559-1), p. 255-262 (disponible sur Internet Archive)
Articles connexes
- Mathématiques arabes
- Liste des mathématiciens arabo-musulmans
- Approximation de π
Liens externes
- (en) John J. O'Connor et Edmund F. Robertson, « Ghiyath al-Din Jamshid Mas'ud al-Kashi », sur MacTutor, université de St Andrews.

- Youcef Guergour, « Le roi de Saragosse Al-Mu'taman Ibn Hūd (m. 1085) et le théorème de Pythagore : ses sources et ses prolongements », LLULL, vol. 28, , p. 415-434 (ISSN 0210-8615, lire en ligne) — p. 430-431 : démonstration par Al-Kashi du théorème qui porte son nom.
- Ressource relative à l'astronomie :
- Notices dans des dictionnaires ou encyclopédies généralistes :
