AccueilFrChercher
Al-Kindi
Ibn Isḥāq al-Kindī
Description de cette image, également commentée ci-après
Portrait d'Al-Kindi.
Nom de naissance Abu Yūsuf Yaʻqūb ibn ʼIsḥāq aṣ-Ṣabbāḥ al-Kindī
(ar) أبو يوسف يعقوب بن إسحاق الصبّاح الكندي
Naissance
Koufa ( Califat abbasside,
actuel Irak)
Décès (71-72 ans)
Bagdad ( Califat abbasside,
actuel Irak)
Résidence Koufa, Bassorah puis Bagdad.
Domaines Philosophie, psychologie, logique, théologie, mathématiques, physique, chimie, astronomie, medecine, pharmacologie, théorie de la musique, cryptanalyse (analyse fréquentielle), calligraphie (arabe).
Institutions Maison de la Sagesse de Bagdad (Bayt al-Hikma)
Influencé par Aristote, Platon, Euclide, Pythagore, Ptolémée, Anthémius de Tralles.
A influencé Abou Ma'shar al-Balkhî, Ahmad ibn al-Tayyib al-Sarakhsi, Abu Zayd al-Balkhi, Isaac Israeli ben Salomon, Miskawayh, Alhazen, Gérard de Crémone, Robert Grossetête, Roger Bacon, Arnaud de Villeneuve, Bernard de Gordon.
Renommé pour promoteur de la philosophie de l'Antiquité grecque, fondateur de la philosophie islamique, nombreux traités scientifiques et philosophiques.

Abū Yūsuf Yaʿqūb ibn Isḥāq al-Kindī (en arabe : أبو يوسف يعقوب بن إسحاق الكندي ) (Koufa, 801 – Bagdad, 873)[1], plus connu sous son nom latinisé d'Alkindus ou Al-Kindi, est considéré comme l'un des plus grands philosophes arabes « hellénisants » (faylasûf)[2], en étant surnommé « le philosophe des Arabes »[3],[4].

« Il fut le premier à faire une synthèse originale entre la pensée grecque et la pensée religieuse musulmane. » (A. Badawi, Histoire de la philosophie en islam, p. 477)

Esprit encyclopédique, il a cherché à synthétiser, organiser et évaluer l'ensemble des savoirs de son temps, en s'intéressant à des domaines très variés : philosophie, mathématiques, astronomie, physique, chimie, technologie, musique...

Biographie

Sa date de naissance n'est pas connue avec certitude, les sources la situent autour de 800[5]. Il est issu de la tribu sud arabique de Kindah et naît à Koufa[6],[7], première capitale abbasside. Il fait ses études à Bassorah, dont son père était gouverneur[8], puis à Bagdad, nouvelle capitale abbasside depuis 762. Ces trois villes (Koufa, Bassorah et Bagdad) étaient les plus prestigieuses du monde musulman de l'époque pour leur rayonnement intellectuel[9].

Il bénéficie du mécénat des trois califes mutazilites abbassides, Al-Ma’mūn[5] qui fonde la Maison de la sagesse (Baït al-hikma) en 830, où un grand nombre de traducteurs traduisent en arabe tous les livres disponibles persans, indiens, syriaques et surtout grecs[9]. Puis al-Mu'tassim, qui le nomme précepteur de son fils[5],[10], et à qui il dédie son Kitâb ilâ al-Mu'tasim bi Allâh fî al-falsafah al-ûlâ (« Sur la Philosophie première »)[11], enfin al-Wathiq. Avec ses collègues Al-Khwârizmî et les frères Banou Moussa, il était chargé de la traduction de manuscrits de savants grecs. Il semblerait qu'en raison de ses faibles connaissances en grec, il ait seulement amélioré les traductions faites par d'autres, et ajouté ses propres commentaires aux œuvres grecques[12]. Il aurait ainsi corrigé la Théologie attribuée à tort à Aristote et traduite par Ibn Na'ima al-Himsi (en)[5]. Eustathios (ou Eustâth) a traduit pour lui une partie de la Métaphysique[13].

Dans ce contexte, Al-Kindi devient le précurseur de l'aristotélisme arabe[14]. Si al-Kindi a bénéficié de la liberté de pensée accordée aux savants sous le règne des califes mutazilites, et s'il faut lui reconnaître un penchant pour le mutazilisme[15], il serait cependant réducteur d'identifier la philosophie d'al-Kindi à ce courant théologique[16].

En 847, le nouveau calife Jafar al-Mutawakkil renonce au mutazilisme. Muhammad et Ahmad ibn Moussa, devenus ses rivaux, intriguent pour faire tomber Al-Kindi en disgrâce en 848[17],[10]. Sa bibliothèque est confisquée, mais elle lui sera rendue quelque temps avant sa mort[9], survenue vers 870 (probablement 873)[5].

Philosophie

Contre ceux qui condamnent la pratique de la philosophie, Al-Kindi fait l'éloge de la recherche de la vérité. La vérité scientifique et la vérité révélée ne sont pas en conflit, mais en harmonie[18]. Selon lui, les contempteurs de la raison sont les véritables mécréants[19], car le Prophète recommande de poursuivre la vérité dans les sciences[20]. « Le vrai doit être acquis, quelle que soit sa source »[15].

Sources aristotéliciennes

Al-Kindi reprend la philosophie aristotélicienne, tout en refusant de trop la couper du platonisme. Il reprend chez Aristote la distinction de deux niveaux de réalité : la réalité mouvante et instable sera source d'une connaissance pratique, inférieure. La raison se tournera utilement vers l'intemporel, l'immobile, l'immuable, source de la connaissance la plus pure ; ainsi celle des mathématiques.

Pour étudier la philosophie, il faut commencer par les mathématiques, dans l'ordre suivant : arithmétique, géométrie, astronomie, musique. Cette prééminence donnée à l'étude des mathématiques rappelle Platon[21]. Puis continuer par la logique, la physique et la métaphysique, puis la morale, et enfin toutes les autres sciences qui découlent des premières[22].

« Celui qui veut connaître les démonstrations logiques doit longtemps s'attarder aux démonstrations géométriques et en recevoir les règles[23]. »

Aristote enseignant, miniature d'un manuscrit arabe, Haute-Mésopotamie, XIIIe siècle.

Son Épître des définitions (Risâlah fî hudûd al-ashyâ') précise le sens de termes techniques de la philosophie. Le temps est défini : « une durée dénombrée par le mouvement ». La matière, « sujette à porter les formes », est passive. La nature est « le principe du mouvement ». L'influence d'Aristote est manifeste[24]. Sa reprise de la théorie des quatre causes en témoigne également[15],[25].

Dans son ouvrage Philosophie première, il définit la métaphysique comme « la connaissance de la Réalité Première, Cause de toute réalité »[26]. Le terme de « philosophie première » est celui qu'emploie Aristote, tandis que celui de « métaphysique » a été attribué à une partie de son œuvre par ses éditeurs[27]. La métaphysique viserait la connaissance des raisons des choses, la connaissance physique étant simplement la connaissance des choses et correspondant à l'aristotélisme pur et simple. La physique a pour objet, selon al-Kindi, le mouvement, tandis que la métaphysique étudie ce qui est immuable[28] : « le Vrai premier qui est la cause de tout vrai »[29]. Cette « philosophie première », « science de la Cause première »[25], est une théologie (le Réel premier) dans le cadre d'une « platonisation » et d'une « islamisation » de l'héritage philosophique aristotélicien[30]. La connaissance des Grecs par al-Kindi ne se limite pas au péripatétisme, mais inclut aussi Platon et les néo-platoniciens - en particulier la « Théologie », que l'on croyait d'Aristote, mais qui correspondait à une partie des Ennéades de Plotin[31].

Dieu est l'Un

Al-Kindi reprend dans ce cadre une preuve par Aristote de l'existence de Dieu reposant sur la nécessaire finitude du temps : selon lui, il est impossible d'arriver au temps présent en franchissant une distance de temps infinie : il y aurait donc nécessairement un début. Cette prémisse oblige à postuler l'existence de quelque cause première, qui sera parfaitement et nécessairement une, à la différence de toute chose[14]. Le théologien al-Juwayni, en s'inspirant de cet argument, introduit les méthodes des falasifa dans le kalâm[32].

Dans cette perspective, Dieu se définissait alors comme le Principe Premier de toute chose, l'Un vrai, considéré comme unique, nécessaire et non lui-même causé (immanence), voire infini. Le concept d'Un révèle une influence des néo-platoniciens et renvoie au concept théologique de tawhid (unicité). Selon Al-Kindi, le créateur est un absolument, ce faisant Dieu n'a pas d'attributs distincts de son essence : il n'a ni matière, ni forme, ni qualité, ni relation, ni genre, ni intellect... La partie du livre sur la philosophie première qui a survécu s'achève avec une critique de ceux qui confèrent à Dieu des attributs[33]. C'est l'unité pure créatrice, et en énumérant ce qu'il faut nier de Dieu, Al-Kindi utilise les concepts de la philosophie grecque[9]. C'est aussi un argument en faveur d'une parenté entre al-Kindi et les mutazilites[34].

Al-Kindi s'insère de plain-pied dans la tradition monothéiste, en se maintenant dans les limites de l'Islam : il définit la science prophétique ('ilm ilahi) comme révélation immédiate, tandis que la science humaine ('ilm insani) est progressive et nécessite du temps et des efforts[9],[14]. Mais il n'établit pas de hiérarchie entre elles, puisqu'il les voit comme deux voies différentes pour atteindre la même vérité[18]. Cependant, sa fidélité au Stagirite s'arrête là où la pensée d'Aristote entre en conflit avec le dogme de la création du monde ex nihilo[33]. Al-Kindi rejette l'idée d'une éternité passée et affirme que le monde a un commencement[35]. Il renonce pour la même raison au concept d'émanation des néo-platoniciens, pour penser la création de la Première Intelligence par Dieu, car ce terme suggère que la création est une nécessité, et non un acte de la volonté de Dieu[36]. Il réserve la notion d'émanation pour désigner la naissance de la série des êtres inférieurs[36]. Malheureusement, la partie du livre Sur la philosophie première qui traitait de l'émanation et de la hiérarchie des êtres n'a pas survécu. Il reste que le Dieu d'al-Kindi n'est pas une simple cause motrice, c'est un Dieu créateur, la cause efficiente et créatrice, le seul véritable agent[37]. En outre, alors que le Dieu d'Aristote n'est que pensée de soi-même, al-Kindi, dans une tradition plus plotinienne, conçoit un lien plus étroit entre le créateur et ses créatures, de sorte que Dieu connaît ses créatures. Ainsi, al-Kindi admet la connaissance par Dieu des particuliers, qui sera mise en question par al-Farabi et Avicenne[38].

Al-Kindi et les théologiens

Cependant, il fait du Coran un agent intermédiaire, contingent et créé, puisque Dieu est selon lui sans attributs. Ce qui vaudra à Al-Kindi, quelques dizaines d'années plus tard, la colère de théologiens comme al-Achari [9] n'admettant pas l'idée d'une causalité seconde et indirecte. En effet selon le fondateur de l'acharisme et la tradition sunnite, le Coran, au sens de l'attribut de la parole propre à Dieu, est incréé, et l'action humaine n'a aucune efficacité par elle-même, toute causalité s'expliquant par la volonté de Dieu. Mais les disciples d'al-Ach'ari, al-Baqillani et al-Juwayni, feront une concession au mutazilisme en distinguant la parole éternelle de Dieu de son expression contingente et engendrée[39]. Voilà un second point d'accord entre al-Kindi et le mutazilisme, sur la question, essentielle à son époque, de la création du Coran. Malgré tout, en raison de l'originalité de la pensée du philosophe et des influences multiples qu'il a assimilées, il ne semble pas légitime d'identifier sa pensée à la doctrine mutazilite : « Tout en entretenant des relations étroites avec les mo'tazilites (...), al-Kindi ne faisait pas partie de leur groupe »[40].

De l'âme

Al-Kindi établit que l'âme est distincte du corps, c'est-à-dire qu'elle n'est pas de même nature que lui : quand nous sommes en proie à la colère, l'âme ne parvient pas à dominer cette passion. Cela prouve selon lui que la passion a son origine dans une autre force que l'âme. Dans le cas contraire, l'âme saurait se dominer elle-même. Le conflit suppose le dualisme[41].

Distincte du corps, l'âme peut donc en être séparée. Al-Kindi pense qu'elle est immortelle et que, libérée du corps qui l'entrave, elle atteint après la mort la connaissance de toutes choses. Le discours d'al-Kindi à ce sujet a des accents plotiniens[42]. Son néo-platonisme est patent quand il décrit le parcours des âmes dans l'Au-delà : selon leur degré de perfection morale, elles rejoindront directement le monde divin, ou bien devront d'abord séjourner dans une sphère inférieure pour se purifier et s'élever graduellement jusqu'au plus haut degré[43]. C'est pourquoi al-Kindi exhorte les hommes à prendre soin de leur âme, comme le faisait Platon, en soulignant combien l'âme, éternelle, est plus précieuse que le corps[43].

« Ô homme ignorant et insensé ! Ne sais-tu pas que ton séjour en ce monde n'est que pour un moment ; puis tu iras au véritable monde, et là tu resteras éternellement ? Tu n'es ici-bas que de passage, selon la volonté de ton Créateur [44]! »

Le soin de l'âme est le sujet de la Risala fi al-hila li-daf al-ahzân (« Épître sur les moyens de chasser la tristesse »). Le genre de la consolation est typique de la philosophie grecque des premiers siècles de l'ère chrétienne[45]. Le propos comporte de nombreux thèmes présents notamment chez les stoïciens. On a dit que la lettre n'était qu'une reproduction d'une diatribe de Thémistius. Selon Badawi[46], rien n'est certain, mais les deux écrits ont pu s'inspirer d'une source commune. Miskawaih[47] a écrit un texte comparable. Al-Kindi commence par analyser la cause de la tristesse. Elle est due à notre attachement aux biens de ce monde. Puisque rien n'est impérissable ici-bas, nul n'est à l'abri de la perte de ce qu'il aime. Les biens matériels que nous possédons ne sont pas réellement nôtres, ils nous sont seulement prêtés. Al-Kindi cite Socrate : «Je ne possède pas ce dont la perte m'affligerait ». Les richesses matérielles sont un asservissement. Le sage s'en libère en accordant ses besoins à ses capacités. Pour nous protéger de l'affliction, nous devons donc changer les objets de nos désirs et préférer les biens intellectuels. Immatériels, ils échappent à la corruption. Ils sont toujours accessibles[48].

De l'intellect

En matière de psychologie, al-Kindi a pu recevoir aussi l'influence d'Alexandre d'Aphrodise. Celui-ci, dans le Περι νου (« De l'intellect »), qui fut traduit en arabe[49], distingue trois sortes d'intellects : l'intellect hylique ou matériel, l'intellect-habitus et l'intellect actif[50]. Le premier est passif. C'est l'intellect agent qui le fait passer de la puissance à l'acte. Mais Al-Kindi, dans son traité fi al-ʿaql (traduit en latin sous le titre De intellectu), en distingue quatre[51] : l'intellect en puissance ; l'intellect acquis (al-'aql al-muslafâd) ; l'intellect actif ; l'intellect démonstratif (al-'aql al-bayâni)[52]. En outre, al-Kindi conserve le vocabulaire d'Aristote pour désigner l'intellect en puissance. La question se pose : le philosophe des Arabes, s'il a lu le traité d'Alexandre, s'en est-il inspiré ? Mais A. Badawi écarte l'hypothèse que la notion d'intellect-habitus ou intellect acquis, ait été ajoutée par les auteurs de la traduction arabe d'Alexandre : ce concept est déjà présent dans le De intellectu[53].

La division en quatre intellects sera reprise par al-Farabi puis Avicenne[54].

Le sommeil et le rêve

L'explication du sommeil par al-Kindi est proche de celle d'Aristote ; mais il s'écarte du Stagirite dans sa théorie du rêve[55].

Pour expliquer la cause de l'endormissement, al-Kindi recourt à la théorie des quatre éléments. Le froid et l'humide, qui proviennent d'une moindre activité du corps, ou de la nourriture absorbée, engendrent une détente et un relâchement des sens qui favorisent le sommeil. Celui-ci est défini : « Le sommeil est l'abandon, par l'âme, de l'emploi de tous les sens[56]. » Le sommeil se caractérise par l'inactivité des sens. Mais l'imagination, qui n'a pas besoin d'une matière pour s'exercer, reste active. Jusque-là, l'analyse d'al-Kindi est proche de celle donnée par Aristote dans De somno et vigilia.

Elle s'en écarte quand il avance que l'âme, qui contient les idées intelligibles, parce qu'elle n'est plus limitée par la matière sensible pendant le sommeil, est plus à même de percevoir les réalités intelligibles qu'à l'état de veille. Al-Kindi croit donc à la possibilité pour le songe d'avoir une valeur prémonitoire ou prophétique[57]. Aristote, dans De divinatione per somnum, était plus réservé quant à la faculté prophétique du rêve. Selon lui, l'idée que les rêves sont envoyés par Dieu est réfutée du fait que n'importe qui est sujet au rêve, et pas seulement les plus sages ou les plus saints, qui devraient être distingués[55].

Sciences

Liber novem iudicum in iudiciis astrorum, 1509.

Al-Kindi, à la suite d'Aristote, souligne que la science progresse par accumulation, de sorte que nous sommes redevables à l'égard des Anciens, et notamment des Grecs. Cela rend nécessaire la lecture de leurs écrits[58].

Mais pour Al-Kindi, la lecture des Anciens et la connaissance livresque sont insuffisantes, il faut « suivre la voie des sciences », c'est-à-dire comprendre et évaluer, et pas seulement retenir la lettre. Les commentaires d'Al-Kindi gardent la terminologie antique mais donnent une valeur nouvelle aux anciens concepts, par leur identification et vérification[59].

Ainsi, selon Aristote, la chaleur terrestre est liée au mouvement des sphères célestes, mais comment expliquer alors la formation de la neige et de la grêle dans l'atmosphère ? Al Kindi assouplit la conception des qualités premières : seul le feu est chaud dans l'absolu, l'air n'est chaud que par rapport à l'eau, et l'eau n'est froide que par rapport à l'air. Le froid et le chaud ne sont plus des qualités métaphysiques absolues, mais évaluées dans l'observation des faits. En instaurant des degrés relatifs de qualités, Al-Kindi ouvre la voie à la quantification[59].

Mathématiques et sciences physiques

Al-Kindi écrit de nombreux ouvrages sur l'arithmétique, dont des manuscrits sur les nombres indiens, l'harmonie des nombres, la géométrie des lignes, les multiplications, la mesure des proportions et du temps, les algorithmes.

L'infini

Il écrit aussi sur l'espace et le temps qu'il pense tous les deux finis[60]. Selon lui, comme pour les philosophes grecs, l'existence d'une grandeur infinie conduit à un paradoxe et n'est donc pas possible. Il s'appuie sur la distinction établie par Aristote entre l'acte et la puissance pour démontrer que l'infini ne peut pas exister en acte[61]. Il raisonne ainsi. Imaginons une grandeur infinie. Retirons-en une partie finie. Le reste est-il toujours infini ou bien est-il désormais fini ? De deux choses l'une. S'il est fini, alors, en lui rajoutant la partie finie qu'on lui avait auparavant enlevée, on obtiendrait une grandeur infinie. Mais c'est impossible : l'infini ne peut être la simple addition de grandeurs finies. L'expérience montre qu'en ajoutant un corps fini à un autre fini aussi, on obtient une grandeur finie. Si le reste est infini, en lui rajoutant une grandeur finie, on obtiendrait une grandeur plus qu'infinie. Mais c'est absurde, car l'infini, aux yeux d'al-Kindi, ne saurait être susceptible de degrés : l'infini ne peut pas être plus ou moins infini, pas davantage qu'une grandeur ne peut être plus infinie qu'une autre. Ou bien faudrait-il admettre, ce qui lui semble tout aussi absurde, qu'une grandeur pourrait être additionnée d'une autre sans être augmentée[62]. Par conséquent, il ne peut y avoir d'infini en acte. L'univers est donc fini, et le temps a un commencement[63]. Cependant, al-Kindi n'a pas admis pour autant la thèse atomiste[64].

Géométrie

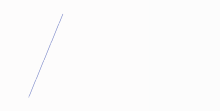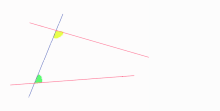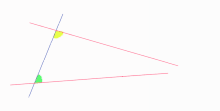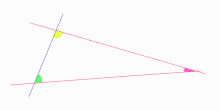
Animation de l'axiome des parallèles ou 5e postulat d'Euclide.

Dans le domaine de la géométrie, il participe à une tradition de recherches sur l'axiome des parallèles d'Euclide. Il donne un lemme sur l'existence concevable de deux lignes droites distinctes dans le plan, à la fois non parallèles et sans intersection, littéralement « qui se rapprochent sans se rencontrer quand elles s'éloignent »[65]. Ce type de recherches peut apparaître comme une étape vers la géométrie non euclidienne[66].

En géométrie sphérique, il montre comment construire un point, étant donnés deux autres points avec leurs distances au premier, sur la même sphère. La construction se fait au compas, réalisant (en termes de géodésie moderne) une construction par intersection linéaire[67].

Optique

Deux de ses œuvres sont consacrées à l'optique géométrique mais, conformément à l'esprit de l'époque, sans séparer clairement la théorie de la lumière de celle de la vision. Il cherche à démontrer la propagation rectiligne des rayons lumineux, par l'étude géométrique de l'ombre projetée par un corps éclairé par le passage de la lumière à travers une fente[68], alors qu'Euclide s'était contenté de la postuler[33].

Il s'intéresse aussi à l'étude des « miroirs ardents », au problème d'Anthémius de Tralles de la construction d'un système de miroirs permettant de réfléchir vers un même point les rayons solaires tombant en leur centre. Il traite aussi du problème des couleurs, notamment celle du ciel. Il soutient que l'azur n'est pas la couleur du ciel, mais un mélange d'obscurité et de lumière solaire réfléchie par des particules terrestres dans l'atmosphère[68].

Il a étudié encore la réflexion de la lumière sur les miroirs concaves, et son comportement lorsqu'elle change de milieu (Sur les grandeurs immergées dans l'eau)[69].

Astronomie

L'univers, conformément aux systèmes d'Aristote et de Ptolémée, est constitué d'une série de sphères emboîtées les unes dans les autres. Le Premier Ciel ou Sphère extérieure est la voûte à laquelle sont fixées les étoiles. Au centre se trouve la Terre[70]. Le « philosophe des Arabes » conçoit le monde comme une sphère et rejette, comme Aristote, l'idée du vide[71]. En revanche, il n'admet pas l'idée aristotélicienne de l'éternité du monde, en contradiction avec le Coran, qui en affirme la création ex nihilo[72],[35]. Il s'oppose ainsi également à Proclus, et a pu profiter de l'influence de Jean Philopon[73],[15]. Par cette thèse, il se distingue des autres falasifa comme al-Farabi et Avicenne. La Sphère extrême est un corps vivant et doué de raison. Elle a elle-même été créée du néant. Elle est la cause de tout ce qui existe dans les cieux inférieurs. C'est pourquoi elle doit être douée de vie et de raison : la cause ne peut pas être dépourvue des qualités de ses créatures[74].

Al-Kindi admet la théorie des quatre éléments, mais il affirme que le Premier Ciel n'en est pas constitué. La Sphère des sphères n'est pas de même nature que les éléments. Il en veut pour preuve qu'ils ne sont pas animés du même typede mouvement. Les éléments connaissent un mouvement fini : quand un élément a rejoint son lieu naturel, il s'arrête ; alors que le mouvement du Premier Ciel, circulaire, est un mouvement de rotation éternel (a parte post)[75].

Il s'intéresse au problème mathématique de l'apparition du croissant de lune, en montrant que le moment de cette visibilité ne peut être qu'approché[76]. Il a traduit en arabe le commentaire de Théon d'Alexandrie sur l'Almageste de Ptolémée[77].

Hydrostatique

En hydrostatique, il ramène la théorie des corps creux flottant (bateaux) à celle des corps flottants pleins (bateaux chargés)[78].

Autres

Al-Kindi (vue d'artiste)
Al-Kindi (vue d'artiste).

En chimie, il traite des huiles essentielles obtenues par distillations de végétaux, dans son Épître de la chimie des parfums et des distillations, où l'on trouve 107 recettes de fabrications avec la description des instruments utilisés[79]. Dans son Épître sur les épées, il traite de l'obtention de l'éclat de l'acier (acier de Damas)[80],[81]. En revanche, comme Avicenne, il s'oppose résolument à l'alchimie de transmutation des métaux considérée comme impossible, dans Le livre de la mise en garde contre les tromperies des chimistes[82].

En médecine, dans le domaine pharmaceutique, il tente d'établir des règles mathématiques pour déterminer l'effet final d'un remède composé, à partir de la quantité et des degrés de qualité[83] de chaque ingrédient[84].

Dans ses ouvrages sur la théorie musicale, il met en évidence comme Pythagore que les sons produisant des accords harmonieux ont chacun une hauteur précise. Le degré d'harmonie dépend de la fréquence des sons. Son traité décrit la touche du oud ou luth à manche court, accordé par quartes (théorie des sept doigtés). Le système préconisé par Al-Kindi est un système pythagoricien simple[85].

Il écrit le premier ouvrage connu de cryptanalyse, le Manuscrit sur le déchiffrement des messages codés, retrouvé en 1987 dans les archives ottomanes d'İstanbul[86]. Cet ouvrage présente la technique d'analyse fréquentielle des lettres du texte chiffré. L'administration du califat abbasside, pour cacher les informations à qui elles n'étaient pas destinées, avait recours au chiffrement par substitution[86]. La méthode d'analyse fréquentielle repose sur l'analyse statistique. Elle consiste à établir la fréquence de chaque lettre dans l'alphabet puis de comparer avec leur fréquence d'apparition dans le message à décrypter. Ce faisant, Al-Kindi développe des calculs déjà pratiqués par le lexicographe Al-Khalil (analyse phonologique avec arrangements et combinaisons de lettres). L'analyse combinatoire réunit les linguistes et algébristes dans l'étude de la langue du Coran en s'appliquant aux domaines de la phonologie, de la lexicographie et de la cryptographie[87].

Œuvres

L'apocryphe De radiis, manuscrit, XVIIe siècle. Cambridge, Trinity College Library, Medieval manuscripts, MS R.15.17 (937).

Il a écrit près de 250 à 290 ouvrages[88], généralement sous la forme de brefs traités, mais une trentaine seulement nous sont parvenus. Les principaux se répartissent dans les domaines suivants[22] : géométrie (32 ouvrages), philosophie (22), médecine (22), astronomie (16), physique (12), arithmétique (11), logique (9), musique (7), psychologie (5).

Il traite aussi de théologie islamique, mais relativement peu[22]. Dans De la philosophie première (Kitab fî al-falsafah al-ûlâ), il écrit que la vérité doit être acquise de quelque source qu'elle provienne[89], et que les enseignements de la philosophie sont identiques au message du Prophète[15].

Il a écrit encore sur la minéralogie et la joaillerie[90] - son grand-père était bijoutier[91], la météorologie[92],[93], le phénomène des marées[94], la verrerie et les parfums[15].

Postérité

Son traité De intellectu a eu une influence importante sur les philosophes musulmans : al-Farabi et Avicenne[13],[54].

Gérard de Crémone (1114-1187) a traduit en latin plusieurs ouvrages d'Al Kindi, dont ceux de pharmacologie (De gradibus) et d'optique (De aspectibus).

Arnaud de Villeneuve (1240-1311) et Bernard de Gordon ont poursuivi les recherches d'Al Kindi dans le domaine pharmacologique.

Al Kindi est cité par des auteurs de la Renaissance, comme Marsile Ficin ou Cornelius Agrippa, lors des discussions universitaires sur l'alchimie, l'astrologie et la magie[95].

Giordano Cardano (De subtilitate) voit en lui l'un des douze esprits les plus brillants de l'histoire de l'humanité[51],[96].

Le "concours Alkindi", organisé annuellement en France pour les classes de 4e, 3e et 2nde, est une compétition de cryptographie nommée en l'honneur du penseur[97].

Bibliographie

Ouvrages traduits

Première page du Manuscrit sur le déchiffrement des messages cryptographiques.
  • Œuvres philosophiques et scientifiques d'Al-Kindi, tome 1 : L'Optique et la catoptrique d'al-Kindî ; éd. Roshdi Rashed. Leyde, Brill, 1997. (ISBN 978-9004-09781-0), DOI 10.1163/9789004450462
  • Œuvres philosophiques et scientifiques d'Al-Kindi, tome 2 : Métaphysique et cosmologie ; éd. Roshdi Rashed. Leyde, Brill, 1998. (ISBN 978-9004-11073-1), DOI 10.1163/9789004450998
  • Cinq épîtres, CNRS, 1976, 101 p. Épître des définitions (Risala fi hudud), Propos succinct et bref sur l'âme, Traité sur la quiddité du sommeil et de la vision, De ce qu'il y a des substances incorporelles, De l'unicité de Dieu et de la finitude du corps du monde.
  • Épître sur le discours sur l'âme (Al-qawl fî al-nafs), trad. espagnole in Obras filosoficas, Madrid, 1968, p. 134-138. (Influence de la Théologie du Pseudo-Aristote).
  • Le moyen de chasser les tristesses et autres textes éthiques, trad. S. Mestiri et G. Dye, Fayard, 2004, 136 p.
  • De mutatione temporum (De la mutation des temps), éd. G. Bos, Ch. Burnett, London - New York, 2000 (textes arabe, hébreu, latin).
  • The Forty Chapters, éd. Charles Burnett, Cambridge : Cambridge University Press , 1993. (Sur l'astrologie).
  • (Apocryphe) De radiis stellarum (Des rayons stellaires) ou Stellatis ou Theorica artium magicarum. Édition (latine) par Marie-Thérèse d'Alverny et Françoise Hudry, De radiis, in : Archives d'histoire doctrinale et littéraire du Moyen Âge, 41 (1974), p. 139-260, texte p. 215-260. Trad., notes de Sylvain Matton, in La magie arabe traditionnelle, Paris, Retz, 1977, p. 70-128. Trad. D. Ottaviani, Al-Kindi. De radiis. Théorie des arts magiques, Allia, 2003. Le caractère apocryphe de ce traité a été démontré par Jean Jolivet dans son compte rendu de l'ouvrage de Pinella Travaglia, Magic, Causality and Intentionality. The Doctrine of Rays in al-Kindī, Florence 1999, in Cahiers de civilisation médiévale, 45e année (n° 180), Octobre-décembre 2002, p. 405-408 [lire en ligne], et par Sylvain Matton dans "D'un rayonnement des grammairiens latins, ou le De radiis n'est pas d'al-Kindi", où il est montré que le De radiis a été composé par un auteur latin entre 1250 et 1270 [lire en ligne].
  • De aspectibus (Des aspects), édi. par Björnbo et al., apud Drei Optische Werke, Leipzig, Teubner, 1912. Optique.
  • De gradibus medicinarum (Des doses pour les médicaments) ou Quia primos, trad. en latin apud Opuscula illustrium medicorum de dosibus, Lyon, 1584. Trad. Léon Gauthier, Antécédents gréco-arabes de la psycho-physique, Beyrouth, 1939, p. 44-91. Pharmacologie.
  • De quinque essentiis (Sermo de tempore, en arabe Fi al-jawhar al-khamsa). Sur la matière, la forme, le mouvement, l'espace et le temps)[98].
  • Le petit traité fî al-'aql est traduit et publié par Abderrahman Badawi dans son Histoire de la philosophie en islam, p. 447-450. [lire en ligne (page consultée le 29 juillet 2022)].

Études

  • Peter Adamson, Al-Kindi, Oxford, Oxford University Press, coll. "Great Medieval Thinkers", 2006.
  • A. Badawî, Histoire de la philosophie en terre d'Islam, Vrin, 1972, t. II, p. 385-477.
  • Gerritt Bos et Charles Burnett, Scientific weather forecasting in the middle ages : the writings of Al-Kindī : studies, editions, and translations, Kegan Paul, 2000.
  • Pinella Travaglia, Magic, Causality and Intentionality. The Doctrine of the Rays of al-Kindî, Florence, Sismel/Edizioni del Galluzzo, coll. "Micrologus", 1999, 176 p.

Notes et références

  1. ↑ (arabe : أبو يوسف يعقوب ابن إسحاق الكندي)
  2. ↑ « Al-Kindī fut, certes, le premier des grands philosophes hellénisants de langue arabe ou falāsifa, mais également un savant prodigieux doté d'une culture proprement encyclopédique. » Salah Ould Moulaye Ahmed, L'apport scientifique arabe à travers les grandes figures de l'époque classique, UNESCO, coll. « Histoire plurielle », , 274 p. (ISBN 92-3-203975-3, lire en ligne), p. 51.
  3. ↑ Encyclopædia Universalis, « KINDI AL », sur Encyclopædia Universalis (consulté le )
  4. ↑ Louis Gardet, M. M. Anawati et Georges C. Anawati, Introduction à la théologie musulmane: essai de théologie comparée, J. Vrin, (lire en ligne), p. 74
  5. 1 2 3 4 5 ʻAbd al-Raḥmān Badawī, Histoire de la philosophie en Islam, J. Vrin, (lire en ligne), p. 386
  6. ↑ Henry Corbin, « Histoire de la philosophie islamique. (1964 edition) » Inscription nécessaire, sur Open Library, (consulté le ), p. 217
  7. ↑ Selon Abderrahman Badawi, Histoire de la philosophie en islam, p. 386, il est né peut-être à Bassora ou, plus probablement, à Koufa. https://www.google.fr/books/edition/Histoire_de_la_philosophie_en_Islam/I0ANAAAAIAAJ?hl=fr
  8. ↑ Jean Jolivet, dans l'article de l'Encyclopædia Universalis comme Henry Corbin dans son Histoire de la philosophie islamique, p. 217, l'affirment. Mais pour Badawi (Histoire de la philosophie en islam, p. 386), son père était gouverneur de Kufa, et c'est dans cette ville qu'il serait né. De même pour Al-Jubouri, dans History of Islamic Philosophy, p. 199.
  9. 1 2 3 4 5 6 Jean Jolivet, Kindi (Al-), t. 10, Encyclopedia Universalis, , p. 851-852.
  10. 1 2 Al-Kindi, Oeuvres philosophiques et scientifiques d'Al-Kindī: Métaphysique et cosmologie. vol. II, BRILL, (ISBN 978-90-04-11073-1, lire en ligne), p. vii
  11. ↑ Badawi, Histoire de la philosophie en islam, p. 388.
  12. ↑ Badawi, Histoire de la philosophie en islam, p. 395-396.
  13. 1 2 H. Corbin 1964, p. 218.
  14. 1 2 3 Abdurraman Badawi, Philosophie et théologie de l'Islam à l'époque classique, Hachette, , p. 121-123.
    dans La philosophie médiévale, François Châtelet (dir.).
  15. 1 2 3 4 5 6 J. Jolivet et R. Rashed. «Al-Kindi» in Encyclopædia of islam, Brill, 1986, vol. V, p. 122.
  16. ↑ (en) I. M. N. Al-Jubouri, History of Islamic Philosophy: With View of Greek Philosophy and Early History of Islam, Authors On Line Ltd, (ISBN 978-0-7552-1011-4, lire en ligne), p. 199
  17. ↑ Badawi, Histoire de la philosophie en islam, p. 387.
  18. 1 2 H. Corbin 1964, p. 219-220.
  19. ↑ Al-Kindi, Oeuvres philosophiques et scientifiques d'Al-Kindī: Métaphysique et cosmologie. vol. II, BRILL, (ISBN 978-90-04-11073-1, lire en ligne), p. 14
  20. ↑ A. Badawi 1972, p. 403.
  21. ↑ Al-Jubouri, History of islamic philosophy, p. 202.
  22. 1 2 3 Jean Jolivet, Classification des sciences, Seuil, (ISBN 978-2-02-062028-4), p. 256-258.
    dans Histoire des sciences arabes, vol. 3, Technologie, alchimie et sciences de la vie, Roshdi Rashed (dir.).
  23. ↑ A. Nagy. Die philosophischen Abhanglunden des Ja'qub ben Ishaq al-Kindi, cité par Émile Bréhier, Histoire de la philosophie, tome I, livre III, chap. IV, p. 547.
  24. ↑ Badawi 1972, p. 402.
  25. 1 2 Al-Kindi (trad. Rushdī Rāshid), Oeuvres philosophiques et scientifiques d'Al-Kindī: Métaphysique et cosmologie. vol. II, BRILL, (ISBN 978-90-04-11073-1, lire en ligne), p. 10
  26. ↑ Thomas d'Aquin fera de même en des termes à peine différents au début de sa Somme théologique.
  27. ↑ Aristote, Métaphysique. Introduction par Jean Tricot, p. 23. https://philosophie.cegeptr.qc.ca/wp-content/documents/M%C3%A9taphysique.pdf
  28. ↑ A. Badawi 1972, p. 406.
  29. ↑ Al-Kindi (trad. Roshdī Rāshed), Oeuvres philosophiques et scientifiques d'Al-Kindī: Métaphysique et cosmologie. vol. II, BRILL, (ISBN 978-90-04-11073-1, lire en ligne), p. 8
  30. ↑ Christian Jambet, Qu'est-ce que la philosophie islamique ?, Gallimard, coll. « folio essais » (no 547), (ISBN 978-2-07-033647-0), p. 255.
    Pour l'analyse détaillée de la philosophie première d'Al-Kindi, voir p. 255-263.
  31. ↑ Badawi 1972, p. 398-400.
  32. ↑ Badawi, Histoire de la philosophie en islam, p. 362.
  33. 1 2 3 Jolivet et Rashed, Encyclopédie de l'islam, p. 123.
  34. ↑ Mohyddin Yahiya, La pensée classique arabe. 3, L'aurore du kalâm, p. 24. (Lire en ligne)
  35. 1 2 (en) Tony Abboud, Al Kindi: The Father of Arab Philosophy, The Rosen Publishing Group, Inc, (ISBN 978-1-4042-0511-6, lire en ligne), p. 50
  36. 1 2 H. Corbin 1964, p. 220.
  37. ↑ A. Badawi 1972, p. 417.
  38. ↑ Al-Kindi, Oeuvres philosophiques et scientifiques d'Al-Kindī: Métaphysique et cosmologie. vol. II, BRILL, (ISBN 978-90-04-11073-1, lire en ligne), p. 133
  39. ↑ Badawi 1972 p. 375.
  40. ↑ Corbin 1964, p. 219.
  41. ↑ A. Badawi 1972, p. 427.
  42. ↑ A. Badawi 1972, p. 430.
  43. 1 2 A. Badawi 1972, p. 430-431.
  44. ↑ Al-Kindi. Rasâ'il al-Kindi al-falsafyyah, édité par Abû Ridâ, cité par Badawi, Histoire de la philosophie en islam, p. 431.
  45. ↑ Émile Bréhier, Histoire de la philosophie. I, Antiquité et Moyen Âge, PUF, (ISBN 9782130523826), p. 369 et suivantes
  46. ↑ A. Badawi 1972, p. 456.
  47. ↑ A. Badawi 1972, p. 477.
  48. ↑ A. Badawi donne une « paraphrase assez complète » du texte d'al-Kindi dans son Histoire de la philosophie en islam, pages 457 à 469.
  49. ↑ A. Badawi 1972, p. 437.
  50. ↑ A. Badawi 1972, p. 435-436.
  51. 1 2 H. Corbin 1964, p. 221.
  52. ↑ A. Badawi 1972, p. 438.
  53. ↑ A. Badawi 1972, p. 444.
  54. 1 2 A. Badawi 1972, p. 439.
  55. 1 2 A. Badawi 1972, p. 453.
  56. ↑ A. Badawi 1972, p. 450.
  57. ↑ A. Badawi 1972, p. 452.
  58. ↑ A. Badawi 1972, p. 402.
  59. 1 2 René Taton, Histoire générale des sciences, t. I : La science antique et médiévale, PUF, , partie III, chap. II (« La science arabe »), p. 454-456.
  60. ↑ Comparer à la notion d'aevum chez Thomas d'Aquin
  61. ↑ A. Badawi 1972, p. 404.
  62. ↑ A. Badawi 1972, p. 408-409.
  63. ↑ A. Badawi 1972 p. 410.
  64. ↑ G. Vajda, « Review of Al-Kindi's Metaphysics. A Translation of Yaʿqūb ibn Isḥāq al-Kindī's Treatise " On First Philosophy (fi al-Falsafah al-Ūlā) », Arabica, vol. 23, no 1,‎ , p. 107 (ISSN 0570-5398, lire en ligne, consulté le )
  65. ↑ Le mathématicien Al-Biruni reprend un raisonnement d'Al-Kindi selon lequel « la propriété des quantités de pouvoir être divisées à l'infini est semblable à la situation de deux lignes droites se rapprochant sans se rencontrer quand elles s'éloignent ». Roshdi Rashed 1997, Histoire des sciences arabes, vol. 2, p. 139-140. Pour l'histoire de la théorie des parallèles en géométrie arabe, voir p. 135-142.
  66. ↑ Ahmed Djebbar, Une histoire de la science arabe, Seuil, (ISBN 2-02-039549-5), p. 217-218.
  67. ↑ Boris A. Rosenfeld, Géométrie, Seuil, (ISBN 978-2-02-062027-7), p. 153.
    dans Histoire des sciences arabes, vol. 2, Mathématiques et physique, Roshdi Rashed (dir.).
  68. 1 2 Roshdi Rashed, L'optique géométrique, Seuil, (ISBN 978-2-02-062027-7), p. 299-305.
    dans Histoire des sciences arabes, vol. 2, Mathématiques et physique, Roshdi Rashed (dir.).
  69. ↑ Kindī, Oeuvres Philosophiques Et Scientifiques D'Al-Kindi: L'Optique Et La Catoptrique, BRILL, (ISBN 978-90-04-09781-0, lire en ligne), p. XI-XII
  70. ↑ A. Badawi 1972, p. 418-419.
  71. ↑ Al-Jubouri 2004, p. 212.
  72. ↑ Al-Jubouri 2004, p. 205-206.
  73. ↑ Badawi, Histoire de la philosophie en islam, p. 414.
  74. ↑ A. Badawi 1972, p. 420-422.
  75. ↑ A. Badawi 1972, p. 423-425.
  76. ↑ Djebbar 2001, op. cit., p. 167.
  77. ↑ Régis Morelon, L'astronomie arabe orientale (VIIIe – XIe siècle), Seuil, (ISBN 978-2-02-062025-3), p. 38.
    dans Histoire des sciences arabes, vol. 1, Astronomie théorique et appliquée, Roshdi Rashed (dir.).
  78. ↑ Djebbar 2001, p. 251-252.
  79. ↑ Djebbar 2001, op. cit., p.344-346.
  80. ↑ Taton 1966, op. cit. p. 505.
  81. ↑ Djebbar 2001, op. cit., p. 363-364.
  82. ↑ Djebbar 2001, op. cit., p. 358 et 360.
  83. ↑ selon les 4 degrés des 4 qualités de la théorie humorale de Galien.
  84. ↑ (en) N.G. Siraisi, Medieval & Early Renaissance Medicine, The University of Chicago Press, (ISBN 0-226-76130-4), p. 146.
  85. ↑ Jean-Claude Chabrier, Science musicale, Seuil, (ISBN 978-2-02-062027-7), p. 248-249.
    dans Histoire des sciences arabes, vol. 2, Mathématiques et physique, Roshdi Rashed (dir.)
  86. 1 2 Simon Singh, Histoire des codes secrets: De l'Egypte des Pharaons à l'ordinateur quantique, JC Lattès, (ISBN 978-2-7096-4421-1, lire en ligne)
  87. ↑ Roshdi Rashed, Analyse combinatoire..., Seuil, (ISBN 978-2-02-062027-7), p. 56.
    dans Histoire des sciences arabes, vol. 2, Mathématiques et physique, Roshdi Rashed (dir.).
  88. ↑ Environ 270 selon le Fihrist («l'index» ou «le catalogue») d'al-Nadîm ("KINDĪ AL-" in Encyclopædia Universalis en ligne).
  89. ↑ Al-Kindi, Oeuvres philosophiques et scientifiques d'Al-Kindī: Métaphysique et cosmologie. vol. II, BRILL, (ISBN 978-90-04-11073-1, lire en ligne), p. 12
  90. ↑ Abdelali Elamrani-Jamal, « Mineralogie Al-Kindi 2004 Ori » Inscription nécessaire [PDF], sur Scribd (consulté le )
  91. ↑ Clifford Edmund Bosworth, Encyclopedie De L'Islam: Supplement - Livr, 3-4 Batriyya-Diawhar, Brill Archive, (ISBN 978-90-04-06381-5, lire en ligne), p. 252
  92. ↑ A. Badawi 1972, p. 390.
  93. ↑ Al-Jubouri, History of islamic philosophy, p. 212.
  94. ↑ Al-Jubouri, History of islamic philosophy, p. 215.
  95. ↑ (en) Brian P. Copenhaver, Astrology and magic, Cambridge University Press (ISBN 0-521-25104-4), p. 266 et 285.
    dans The Cambridge History of Renaissance philosophy, Charles B. Schmitt (dir.).
  96. ↑ Abboud 2006, p. 101.
  97. ↑ « Concours Alkindi », sur www.concours-alkindi.fr (consulté le )
  98. ↑ Jean Jolivet, « Al-kindī, vues sur le temps », Arabic sciences and philosophy,‎ (lire en ligne Accès payant)

Articles connexes

  • Mathématiques arabes
  • Liste des mathématiciens arabo-musulmans
  • Mutazilisme
  • Juan Vernet

Liens externes