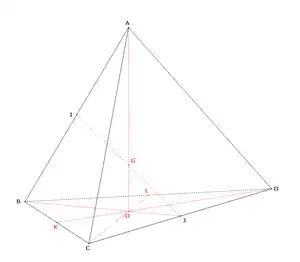
En mathématiques, le barycentre d'un ensemble fini de points du plan ou de l'espace est un point qui permet de réduire certaines combinaisons linéaires de vecteurs. Les coordonnées de ce barycentre dans un repère cartésien correspondent alors aux moyennes arithmétiques des coordonnées homologues de chacun des points considérés, éventuellement affectés des coefficients de pondération. Lorsque ces coefficients de pondération sont égaux, le barycentre est appelé isobarycentre, et généralise ainsi la notion de centre de gravité d’un triangle.
La notion de barycentre est utilisée en physique notamment pour déterminer le point d'équilibre d'un ensemble fini de masses ponctuelles.
Plus généralement, le barycentre peut se définir dans le cadre d'un espace affine sur un corps quelconque. Le barycentre est un outil central en géométrie affine qui permet de caractériser et étudier les sous-espace affines, les applications affines et la convexité.
La version continue de la notion du barycentre est celle de centre de masse, qui traduit la notion correspondante de centre d'inertie pour un solide en mécanique classique.
Historique et origine physique
Le terme de barycentre est formé sur la racine grecque βαρυσ / barys (pesant, lourd) pour désigner un centre des poids ou centre d'équilibre. Sa conception est liée au théorème des moments découvert par Archimède au IIIe siècle av. J.-C. Il écrit dans son traité De l’équilibre de figures planes :
« Tout corps pesant a un centre de gravité bien défini en lequel tout le poids du corps peut être considéré comme concentré. »
Son principe des moments et des leviers permet de déterminer assez simplement le barycentre O de deux points de masses m1 et m2 différentes.

Pour que la balance soit en équilibre, il faut que les moments m1⋅OA⋅g et m2⋅OB⋅g soient égaux dans le champ de pesanteur g. Si par exemple la masse m1 est 4 fois plus importante que la masse m2, il faudra que la longueur OA soit 4 fois plus petite que la longueur OB. Cette condition se traduit par l'égalité vectorielle
Ce principe des moments est d'ailleurs utilisé dans la balance dite romaine.
Les poids apparents peuvent également avoir une valeur numérique négative, si l'une des masses est remplacée par un ballon d'hélium, par exemple : la poussée d'Archimède s'ajoute au poids et la résultante est une force pouvant s'exercer vers le haut. Dans ce cas, le point d'équilibre se situe en dehors de l'espace délimité par les deux objets.
Barycentre de deux points dans le plan
Définition du barycentre par une relation vectorielle
On définit le barycentre de deux points A et B du plan affectés des coefficients de pondération a et b (avec la somme a + b non nulle) comme l'unique point G vérifiant la relation vectorielle
En effet, à l'aide de la relation de Chasles, cette relation peut se réécrire sous la forme
c'est-à-dire
ou de manière équivalente
Comme la somme a + b est non nulle, il existe donc un unique point G qui satisfait cette équation. Il est donné par la relation
On dit alors que G est le barycentre des points A et B affectés des coefficients de pondération a et b ; on note G = bar{(A,a),(B,b)}. On remarque, d'après l'égalité vectorielle ci-dessus que G appartient à la droite (AB).
La réciproque est d'ailleurs vraie : tout point de la droite (AB) peut être considéré comme un barycentre des points A et B
Si les coefficients de pondération sont de même signe le barycentre des points A et B sera situé sur le segment [AB]
Dans le cas particulier où a = b, on parle plutôt d'isobarycentre. Dès lors, l'isobarycentre de deux points A et B correspond au milieu de ces deux points.
Les points A et B étant donnés, la construction géométrique du barycentre G de ces deux points se fait grâce au théorème de Thalès.
Certains logiciels de géométrie dynamique (LGD) définissent G=bar{(A,a),(B,b)} par G = a*A+b*B
Colinéarité
De la définition
on tire que
ou encore que
En d'autres termes, ces deux vecteurs sont colinéaires. Ils ont de plus un point en commun, G. Par conséquent, G appartient à la droite (AB). Ainsi
- si G est le barycentre de {(A,a),(B,b)} alors G appartient à la droite (AB).
Si G est sur le segment [AB] (entre A et B) alors
pour un certain k< 0 puisque ces deux vecteurs sont de sens opposé. Mais, comme dans le même temps
on en déduit que b et a sont de même signe. Ainsi
- Si G est sur le segment [AB] (entre A et B) alors a et b sont de même signe.
Homogénéité
Si G est le barycentre de {(A,a),(B,b)} alors
et il vient que pour tout réel k on a
Autrement dit, on obtient
De plus, comme a+b est non nul, pour tout k réel non nul, k(a+b) est également non nul. Alors G est le barycentre de {(A,ka),(B,kb)}. Ainsi
- si G est le barycentre de {(A,a),(B,b)} alors pour tout k réel non nul, G est aussi le barycentre de {(A,ka),(B,kb)}.
Autrement dit le barycentre de deux points reste inchangé si les coefficients de pondération de ces points sont multipliés par un même réel.
Cette propriété du barycentre s'appelle l'homogénéité.
Réduction
L'application de la relation de Chasles
en introduisant le barycentre G de {(A,a),(B,b)} donne
G étant barycentre de {(A,a),(B,b)} alors :
La relation précédente devient:
Ainsi
- si G est le barycentre de {(A,a),(B,b)} alors pour tout point M du plan,
- .
C'est la propriété dite de réduction, ou réduction de somme vectorielle.
Elle permet de positionner le point G par rapport à tout point M. Si M est l'origine d'un repère du plan ou de l'espace, elle permet de définir les coordonnées (xG,yG) du point G dans ce repère en fonction des coordonnées (xA,yA) et (xB,yB) des points A et B dans ce repère:
Barycentre de trois points dans le plan ou dans l'espace
La définition peut se généraliser à trois points du plan ou de l'espace : pour tous réels a, b et c tels que a + b + c soit non nul, il existe un unique point G tel que
appelé barycentre du système pondéré {(A,a),(B,b),(C,c)}. Les points G, A, B et C sont toujours coplanaires et on démontre que, si A, B, C définissent un plan, tous les points M de ce plan peuvent s'écrire comme barycentre de A, B et C. Les pondérations s'appellent alors coordonnées barycentriques de M dans le repère A, B et C.
Dans le cas particulier où a = b = c, on parle plutôt d'isobarycentre que de barycentre.
Comme pour le barycentre de deux points, le barycentre de trois points permet de réduire l'expression vectorielle
pour tout point M :
Cela permet, en remplaçant M par l'origine du repère, de donner les coordonnées (xG,yG,zG) du point G dans ce repère en fonction des coordonnées (xA,yA,zA), (xB,yB,zB) et (xC,yC,zC) des points A, B et C dans ce repère:
Le barycentre possède en outre une propriété dite d'associativité ou de barycentre partiel : si a + b est non nul et si H est le barycentre du système {(A,a),(B,b)}, alors G est le barycentre du système {(H,a+b),(C,c)}. Cela signifie que la construction du barycentre de trois points peut se ramener à la construction de barycentres de deux points. Cette propriété simplifie grandement les problèmes d'alignement et de concours.
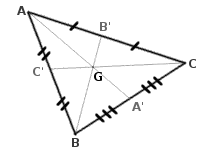
En considérant trois points A, B et C distincts et non alignés , le centre de gravité du triangle ABC est par définition le point d'intersection de ses trois médianes. Il est situé aux 2/3 d'une médiane en partant du sommet. Autrement dit, soit un triangle ABC, A' le milieu de [BC], B' le milieu de [AC], et C' le milieu de [AB] et G son centre de gravité. Alors
Ainsi, le centre de gravité du triangle est exactement l'isobarycentre des sommets du triangle, c'est-à-dire que
Remarque : Il existe une encyclopédie de points remarquables d'un triangle ABC : chacun de ces points remarquables est défini comme barycentre des trois points A, B et C
Applications
En géométrie
En géométrie affine, les barycentres (et tout particulièrement les isobarycentres) facilitent grandement les problèmes d'alignement et de concours (trois points sont alignés dès que l'un des points est barycentre des deux autres) et permettent des démonstrations élégantes de théorèmes comme le théorème de Ménélaüs, le théorème de Ceva ou les propriétés du quadrilatère complet.
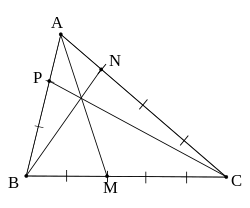
Par exemple, pour le théorème de Ceva, considérons la figure ci-contre (figure 1), les graduations sur chaque côté sont régulières. Le théorème de Ceva affirme que les droites (AM), (BN) et (CP) sont concourantes.
Réduction des fonctions de Leibniz
Grâce à la notion de barycentre, il est possible de réduire des expressions vectorielles.
Prenons l'exemple de 3 points A, B et C de poids a, b et c (de somme non nulle) et considérons le barycentre G de ces trois points. La formule du premier degré est celle du barycentre :
qui permet de nombreux calculs du premier degré sur les vecteurs.
À partir du barycentre il est possible de définir une formule du second degré, au sens du produit scalaire des vecteurs, qui permet de calculer la quantité
Pour cela, remplaçons chaque vecteur par et appliquons la formule du carré d'une somme:
Les doubles produits s'annulent, d'où
au second degré.
En physique
Le barycentre est tout d'abord un outil utilisé pour calculer des points d'équilibre de points matériels, et plus généralement ensuite de centres d'inertie (aussi appelé centre de masse) dans certains cas. La notion même de centre d'inertie peut être vue comme une généralisation du barycentre à un continuum de points matériels.
En effet, si on considère un domaine D de volume fini de l'espace dont la masse volumique au point M est donnée par g(M), alors le centre d'inertie G de D est défini comme le point de l'espace vérifiant
qui généralise la formule
- .
définissant le barycentre G des points matériels Ai de masse ai = g(Ai).
Les coordonnées du centre d'inertie sont données par
qui généralise celles des coordonnées du barycentre G des points matériels Ai de masse ai données par
Dans certains cas particuliers, le calcul du centre d'inertie se ramène à un simple calcul de barycentre. Par exemple, on peut se servir des barycentres pour calculer le centre d'inertie d'une plaque homogène ayant une forme polygonale.
Le barycentre est également utilisé en astronomie. On parle de barycentre en ce qui concerne le couple formé par un corps stellaire et l'un de ses satellites. Le barycentre est le point autour duquel l'objet secondaire gravite.
Généralisation à la notion de barycentre de n points d'un espace affine
Les définitions et résultats énoncés plus haut pour deux ou trois points du plan ou de l'espace usuels se généralisent à n points d'un espace affine E sur un corps (commutatif) K quelconque.
Définition
Soient (A1, … , An) des points de E et soient (a1, … , an) des scalaires (c'est-à-dire d'éléments de K) de somme non nulle.
Le barycentre des points (A1, … , An) affectés des coefficients (a1, … , an) est l'unique point G de E tel que
- .
L'existence et l'unicité de ce point se prouvent aisément en utilisant la relation de Chasles.
On peut noter bar(Ai, ai)i=1, … ,n, ou , ou encore , le barycentre des points (A1, … , An) affectés des coefficients (a1, … , an).
Dans le cas particulier où a1 = a2 = … = an, on parle d'isobarycentre.
Propriétés immédiates
Commutativité : on peut changer l'ordre des points sans changer la valeur du barycentre tant que les points conservent leur coefficient.
Homogénéité : on peut multiplier tous les coefficients par un même scalaire k non nul sans changer la valeur du barycentre. On privilégie alors souvent les coefficients dont la somme vaut 1.
Associativité : si
- ,
on peut définir
et l'on a l'égalité suivante :
- .
Cette propriété se généralise à un regroupement de p sous-familles de coefficients.
Coordonnées barycentriques
Si l'espace affine E est associé à un espace vectoriel V de dimension n, et si (A0,...,An) sont n + 1 points de E, on dit que ces n+1 points forment un repère barycentrique si les vecteurs
forment une base de V. On démontre, grâce à la relation de Chasles, que cette propriété est indépendante de l'ordre des points.
Si (A0,...,An) forment un repère barycentrique de E alors tout point M de E peut être trouvé comme barycentre des (A0,...,An) avec, par homogénéité (voir supra), des coefficients (a0,...,an) de somme 1. Ils sont appelés les coordonnées barycentriques de M.
Variété affine
On appelle variété affine d'un espace affine E toute partie de E stable par barycentres. On démontre que cette définition coïncide avec celle de sous-espace affine.
Le sous-espace affine engendré par une famille de n points (A1,...,An) est le plus petit ensemble contenant ces points et stable par barycentres.
Par exemple, le sous-espace affine engendré par deux points non confondus est une droite affine, et le sous-espace affine engendré par trois points non alignés est un plan affine.
Segments, ensemble convexe
Soit E un espace affine sur R. Si A et B sont deux points distincts de E, l'ensemble des points
où k est un élément de [0, 1], est une partie de la droite (AB) appelé segment [AB]. C'est aussi l'ensemble des points
où a et b sont deux réels positifs (au sens large).
Un ensemble stable par barycentres à coefficients positifs est un ensemble convexe.
L'ensemble des combinaisons convexes des points (A1,...,An), c'est-à-dire de leurs barycentres à coefficients positifs, est l'enveloppe convexe des points (A1,...,An).
Application affine
Soit E1 et E2 deux espaces affines et soit f une application de E1 dans E2. On dit que f conserve le barycentre si pour tout barycentre
de E1, on a
c'est-à-dire que l'image de G par f est le barycentre appartenant à E2 des points f(Ai) affectés des points ai.
La propriété d'associativité du barycentre permet de se limiter à vérifier la conservation pour tout barycentre de deux points.
On démontre que l'ensemble des applications de E1 vers E2 conservant le barycentre coïncide avec celui des applications affines de E1 vers E2.
Certaines applications affines s'expriment bien à l'aide du barycentre. Voici deux exemples.
- Soient A et B deux points, la transformation qui, au point M associe le point
- est une translation, qui a pour vecteur .
- Soient C un point et k un scalaire non nul. La transformation qui au point M associe le point
- est l'homothétie de centre C et rapport k.
Voir aussi
Articles connexes
- Théorème de Leibniz
- Centre de masse (géométrie riemannienne)
- Centre de gravité d'un arc de courbe
- Moyenne pondérée
Bibliographie
- Michèle Audin, Géométrie, EDP Sciences, , 3e éd., 428 p. (ISBN 978-2-7598-0180-0, présentation en ligne), p. 29
- Marcel Berger, Géométrie [détail des éditions] (Tome 1)
- Petite encyclopédie de mathématique, Didier
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4)
- Jean Fresnel, Méthodes modernes en géométrie
- Bruno Ingrao, Coniques projectives, affines et métriques, Calvage & Mounet (ISBN 978-2916352121)
- D. Lehmann et Rudolf Bkouche, Initiation à la géométrie, PUF, 1988 (ISBN 2 13 040160 0)
























































