| Spécialité | Psychiatrie et neuropsychologie |
|---|
| CISP-2 | P24 |
|---|---|
| CIM-10 | F81.2, R48.8 |
| CIM-9 | 315.1, 784.69 |
| MedlinePlus | 001534 |
| MeSH | D060705 |
![]() Mise en garde médicale
Mise en garde médicale
La dyscalculie est un trouble spécifique du développement (tel que la dyslexie, la dyspraxie, la dysorthographie, la dysgraphie, etc., parfois nommés troubles dys-). Elle correspond à un trouble sévère dans les apprentissages numériques, sans atteinte organique, sans troubles envahissants du développement et sans déficience mentale. Des élèves peuvent toutefois rencontrer des difficultés en mathématiques sans présenter de dyscalculie : c'est pourquoi il est important de différencier les difficultés transitoires de l'apprentissage de troubles plus durables.
Étymologie
Le terme scientifique français dyscalculie fut forgé à la fin du XXe siècle à partir du préfixe grec dys-, du radical latin -calcul- et du suffixe français -ie. La dérivation peut s'analyser étymologiquement comme une « difficulté à calculer ».
Le préfixe « dys- » vient du préfixe grec δυσ- / dys- qui exprime « la difficulté, le mal, le manque[1]» (élément abondamment utilisé dans la terminologie médicale : dyslexie, dysorthographie). Le radical -calcul- vient du latin classique calculus (lui-même diminutif de calc(i) — petite pierre) « caillou » notamment de la table à calculer.
Le suffixe français -ie sert à dériver un nom au féminin à partir d'une base nominale. Il est utilisé dans de nombreux troubles neuropsychologiques (agnosie, akinésie, prosopagnosie…).
Description
La notion de dyscalculie remonte au moins à Kosc[2],[3] (1974), qui la définissait comme une déficience spécifique en arithmétique à la suite de dommages ou de déficits de certaines régions spécifiques du cerveau. Cette difficulté en mathématiques se manifeste en l’absence d’une atteinte concomitante des fonctions mentales générales.
Définition
La « dyscalculie développementale » est un trouble qui apparaît dans l'enfance durant la période de l'apprentissage de l'arithmétique et elle doit donc être distinguée de l'acalculie acquise qui elle, survient brutalement à l'âge adulte à la suite d'une lésion cérébrale, le plus souvent un accident vasculaire cérébral. Elle se manifeste chez certains enfants qui, bien qu'ayant une intelligence normale, n'arrivent pas à résoudre une soustraction aussi simple que 7-3 (Dehaene et al.[4]). Ou bien, ces enfants sont incapables d’évaluer à l’œil nu de petites quantités comme deux ou trois objets placés devant eux. Ils ont aussi le plus grand mal à comprendre qu’un nombre puisse être plus grand qu’un autre (comme 9>8).
« La dyscalculie développementale est donc un trouble disproportionné de l'apprentissage de l'arithmétique chez l'enfant, qui ne peut être expliqué par un environnement d'apprentissage appauvri, ni par un niveau intellectuel inférieur. »
— American Psychiatric Association, 1994., Diagnostic and statistical manuel of mental disorders dsm-iv[5]
Ce « trouble de l'apprentissage en arithmétique » peut être détecté chez des enfants avec un QI normal ou supérieur à la moyenne et vivant dans un environnement familial et social normal. Ce trouble se rapproche de la dyslexie, qui se manifeste également par des difficultés d'apprentissage de la lecture chez des enfants qui, eux aussi, ont un QI normal et évoluent dans un environnement familial et social sans problème.
À l'âge adulte, les dyscalculiques continuent à être gênés par leur trouble : souvent, ils ne comprennent pas le prix d'un produit, d'un rabais ou ne savent pas estimer une distance. Ils ont aussi des problèmes d'orientation et des troubles de l'attention.
Le terme de dyscalculie n'est pas utilisé par tous les chercheurs[6]. Le terme de dyscalculie développementale introduit par Kosc (1974) est utilisé par Badian (1983), Shalev et Gross-Tsur (1993, 2001), Butterworth (2005), Dehaene et son équipe[4]. Lewis et al. (1994) préfèrent parler de « difficultés en arithmétique », Geary et Hoard (2005) de « troubles des apprentissages en mathématiques » ou d’« handicap en mathématiques » (mathematic disabilities MD), etc.
Nature des troubles
Pour effectuer des calculs simples, les enfants dyscalculiques utilisent plus souvent et plus longtemps que les enfants n'ayant pas ce trouble, des stratégies primitives de comptage[6]. Par exemple, pour calculer 4+2, ils comptent 1, 2, 3, 4, 5, 6 plutôt que de commencer à 4 et de continuer par 5, 6. Revus dix mois plus tard[7], ces enfants continuent à utiliser cette stratégie alors que les enfants non atteints par ce trouble changent progressivement de stratégie pour recourir de plus en plus souvent à la récupération directe en mémoire. Les difficultés en arithmétique de ces enfants viendraient de leur incapacité à mémoriser et à retrouver les résultats des calculs les plus élémentaires.
Des études plus récentes[8] distinguent les enfants ayant seulement des troubles d’apprentissage en arithmétique (MD) de ceux ayant en outre des troubles en lecture (MD-LD). Les deux groupes utilisent des stratégies primitives telles que le comptage sur les doigts, mais les enfants MD-LD commettent plus d’erreurs que les enfants MD.
Les dyscalculiques recourent plus souvent que les autres à des stratégies primitives et au comptage sur les doigts, le passage à la récupération directe en mémoire étant largement retardé. Ces difficultés pourraient résulter d'une mauvaise compréhension des principes régissant l'activité de dénombrement (compter en pointant avec le doigt un ensemble d’objets), lesquels constituent le socle sur lequel se construiront toutes les habiletés arithmétiques ultérieures.
Classifications
L'hétérogénéité des profils cognitifs des enfants dyscalculiques a conduit les chercheurs et cliniciens à distinguer différents sous-types de dyscalculie.
Rourke propose que les déficiences en arithmétique résultent soit de déficits verbaux, reflétant un dysfonctionnement de l'hémisphère gauche, soit de déficiences non verbales qui résulteraient d'atteintes précoces de l’hémisphère droit[9].
Geary[10] (1993, 2004) a proposé trois sous-types de dyscalculies :
- une « dyscalculie procédurale » dans laquelle les enfants ont du mal à acquérir des stratégies arithmétiques simples (que Geary propose d’associer à un déficit de la mémoire de travail). Les enfants utilisent des procédures immatures de comptage et font preuve d’une faible compréhension des concepts utilisés dans cette activité ;
- un deuxième type est lié à des difficultés dans la « récupération de faits arithmétiques ». Il s’agit de difficultés d’apprentissage des tables (des résultats de tables de multiplication) ou de récupération de résultats d’additions ou soustractions simples (7+4 = ? ; 7-3 = ?). Pour Geary, il s’agirait non pas d’un simple retard de développement mais d’une différence, génétiquement héritable, qui reste inchangée tout au long du développement ;
- une troisième difficulté de nature « visuo-spatiale » : erreurs d’alignement des chiffres en colonnes, confusions de signes arithmétiques (× pour +) ou mauvaise interprétation du rôle de la position dans l’écriture en base 10.
Von Aster[11] propose une classification qui s’appuie sur le modèle du triple code de Dehaene. Suivant ce modèle, l’information numérique peut être manipulée selon trois formats : une représentation analogique codant la magnitude, un code verbal (« trois ») et un code visuel pour les chiffres arabes (« 3 »). Sur cette base, Von Aster distingue trois types de dyscalculies :
- une dyscalculie verbale dans laquelle les enfants éprouvent des difficultés dans la mise en route des procédures de comptage pour effectuer des additions ainsi que pour stocker et récupérer les faits numériques ;
- une difficulté à lire et à écrire les chiffres arabes ;
- un défaut du « sens des nombres » se traduisant par des difficultés dans pratiquement tous les domaines liés aux calculs.
Bases neurologiques de la dyscalculie : l'approche neurocognitive
Il existe très probablement une contribution génétique à la dyscalculie développementale puisque chez les jumeaux homozygotes, si l'un est atteint, dans 70 % des cas l’autre le sera également[12]. Cependant, la transmission génétique de la dyscalculie reste largement méconnue et des facteurs environnementaux pourraient occuper une place importante, en particulier dans les phases précoces du développement cérébral. Il a ainsi été observé une fréquence plus élevée de dyscalculie chez les enfants nés prématurément et chez ceux qui sont exposés pendant la période fœtale à l'intoxication alcoolique de leur mère[4].
Pour Dehaene[13], il existerait deux catégories de compétences numériques :
- une capacité de manipuler les nombres de manière approximative que nous partageons avec des organismes dépourvus de langage comme les rats, les singes ou les nouveau-nés ;
- une capacité arithmétique avancée qui repose sur une notation symbolique des nombres et sur le difficile apprentissage d’algorithmes de calcul exact.
Le système non symbolique, de type analogique donc, qui codifie les quantités approximatives et que l’on retrouve chez les animaux et les jeunes enfants, serait hérité des humains de leurs ancêtres et fournirait une sensibilité aux caractéristiques numériques des groupes d’objets. L’acquisition des capacités symboliques de traitement des nombres qui vient plus tard se baserait sur ce sens primaire des quantités numériques. Le fait que ce système premier du « sens des nombres » vienne à maturité durant la première année de vie du bébé, et qu’il joue un rôle central dans la cognition numérique de l’adulte, en fait pour Wilson et Dehaene[14] un bon candidat pour expliquer le déficit primaire de la dyscalculie.

Les études de neuroimageries IRM[14] ont montré que cette capacité basique à manipuler des quantités de manière approximative et non verbale serait localisée dans la section horizontale du sillon intrapariétal (HIP). Cette région est activée lors des comparaisons de chiffres, des estimations de numérosité, des additions et soustractions approximatives. Cette capacité première du sens des nombres s’observe chez le bébé mais aussi chez l’animal. Nieder et Miller[15] du MIT ont identifié dans le fond du sillon intrapariétal (VIP) du singe macaque des neurones répondant sélectivement à certaines quantités précises de un jusqu’à cinq objets. Or, il existe des homologies entre la région VIP du macaque et la région HIP activée pendant l’arithmétique mentale chez l’homme. La région intrapériétale contiendrait un codage des numérosités qui serait un héritage évolutif. Chez l’homme, après l’apprentissage du langage et de l'écriture, cette même région intrapariétale s'activerait par le biais des notations symboliques des nombres telles que les chiffres arabes[4].
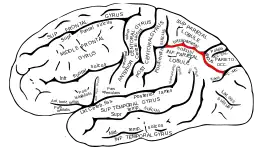
Les tâches de nature plus verbales, comme les multiplications ou les additions exactes, impliquent plutôt le gyrus angulaire gauche. Ce gyrus est aussi le centre lésionnel du syndrome de Gerstmann, qui associe une perte du sens des nombres (acalculie) à un trouble de reconnaissance des doigts (agnosie digitale[N 1]), à une difficulté à distinguer la gauche de la droite et à une dysorthographie. Cette région interviendrait aussi dans la mémorisation des tables de multiplication, réalisée essentiellement par récitation automatique de séquences apprises par cœur.
Enfin, la partie postérieure du lobule pariétal supérieur (PSPL) est activée dans les tâches demandant un déplacement de l'attention spatiale comme les approximations, les soustractions ou la comparaison de nombres.
On ne sait pas encore bien évaluer le rôle des perturbations du sens du nombre dans la dyscalculie développementale. Il est possible qu'il existe plusieurs types de dyscalculie, certaines relevant d'un déficit primaire du système d'évaluation analogique des quantités et d'autres d'une perturbation du système numérique symbolique.
Quelques études commencent à établir la présence d'un sens intuitif des nombres chez les jeunes enfants et à en observer les corrélats neuronaux : ainsi, une étude de neuroimagerie (avec enregistrement de potentiels évoqués) chez des bébés de 2–3 mois a permis de montrer que le cortex intrapariétal était activé à la présentation d'objets dont le nombre varie (Izard[16] et al. 2008).
Pour tester le lien entre sens du nombre et dyscalculie, Piazza et al. (2010) ont utilisé un test psychophysique classique : on présente aux participants deux ensembles de points noirs et on leur demande d'estimer celui qui en contient le plus. Les trois groupes étudiés (enfants d'âge préscolaire, enfants de 10 ans et adultes), discriminent les numérosités de manière semblable suivant la loi de Bouguer-Weber. La mesure de la fraction de Weber w (ou imprécision des représentations) indique cependant une diminution progressive de celle-ci avec l'âge, c'est-à-dire une amélioration du « sens des nombres » avec la scolarisation. Et lorsque la mesure de l'imprécision w est faite sur des enfants dyscalculiques de 10 ans, on retrouve une valeur valant celle d'enfants normaux de 5 ans. De plus, l'importance de l'imprécision des représentations w prédit la dégradation des performances dans les tâches de manipulation de nombres symboliques. Pour les auteurs, ces résultats établissent pour la première fois une association claire entre dyscalculie et déficit du sens des nombres.
Causes
Il est présentement impossible de déterminer si la dyscalculie vient d'un trouble primaire (ou inné) dans le traitement des quantités, ou bien au contraire d'un trouble secondaire lié à la mémoire et au langage.
Les recherches continuent pour trouver les causes de la dyscalculie et elles s’appliquent à plusieurs domaines, entre autres :
- un sous-type de dyscalculie développementale pourrait provenir d'un trouble primaire dans la représentation et la manipulation approximative des quantités (les numérosités) permettant des activités d'estimation et de comparaison de ces numérosités ; aptitudes qui sont à la base du « sens des nombres ». C'est l'hypothèse de Dehaene et son équipe, présentée dans la section ci-dessus ;
- la dyscalculie peut provenir de lésions du gyrus supramarginal et du gyrus angulaire à la jonction entre le lobe temporal et le lobe pariétal du cortex cérébral[17],[18] ;
- des déficiences de la mémoire de travail : Adams et Hitch expliquent que la mémoire de travail est un élément important pour le calcul mental[19]. Sur cette base, Geary réalisa une étude qui suggère que ceux qui souffrent de dyscalculie ont une déficience de la mémoire de travail[20]. Cependant, les problèmes liés à la mémoire de travail se confondent avec des difficultés d’apprentissage plus générales. Autrement dit, les conclusions de Geary peuvent ne pas être spécifiques à la dyscalculie mais peuvent aussi refléter un trouble d’apprentissage plus général.
D’autres causes possibles :
- une mémoire à court terme dérangée ou réduite, rendant difficile de se souvenir des calculs ;
- d'origine congénitale ou héréditaires. Des études laissent à penser son existence[21], cependant, il n’y a pas encore de preuve concrète.
Le syndrome de Gerstmann : la dyscalculie est l’un des nombreux symptômes observés à la suite de lésions du gyrus angulaire. Le sillon intrapariétal peut aussi être impliqué[22].
Les personnes dyscalculiques souffrent souvent, mais pas toujours, de difficultés pour manipuler les dates, les heures, les mesures ou pour raisonner dans l’espace. Bien que certains chercheurs soutiennent que la dyscalculie implique nécessairement à la fois des difficultés de raisonnement mathématique et des difficultés avec les opérations arithmétiques, des travaux (en particulier auprès de personnes ayant un cerveau lésé) ont prouvé que les capacités en arithmétique (c'est-à-dire le calcul et la mémoire des nombres) et en mathématiques (raisonnement abstrait avec des nombres) peuvent être dissociées. En effet, une personne peut souffrir d’un côté de difficultés en calcul (ou de dyscalculie) et d’un autre côté n’avoir aucune déficience (voire parfois même des habiletés) pour le raisonnement mathématique.
Diagnostic
La dyscalculie peut être détectée à un jeune âge et des mesures peuvent être prises pour atténuer les problèmes rencontrés par les jeunes élèves. Le principal problème est de trouver la bonne façon d’enseigner les mathématiques à ces enfants. De même que la dyslexie peut voir ses symptômes atténués en utilisant une méthode d’enseignement légèrement différente, la même approche peut être utilisée pour la dyscalculie. Toutefois, la dyscalculie est le moins connu des troubles d’apprentissage et souvent elle n’est pas repérée et reconnue.
Au Québec, selon la loi 90, la capacité de poser un diagnostic est strictement réservée aux médecins. Cependant, ce trouble peut être évalué et rééduqué par des orthophonistes et des neuropsychologues. L'évaluation va pouvoir démontrer l'hypothèse diagnostique de dyscalculie chez la personne et cette évaluation pourrait aider les médecins à poser leur diagnostic. Une prise en charge précoce permettra de pallier les difficultés de la personne, ce qui favorisera une meilleure insertion au quotidien (et notamment à l'école et au moment de son orientation).
Prévalence
- Selon les estimations actuelles, la dyscalculie peut affecter entre 3,6 et 7,7 % de la population[6] (taux de prévalence sur des populations d'enfants d'âge scolaire). Ces différences importantes tiennent aux seuils des critères d'inclusion plus ou moins stricts (score au test de retard scolaire) ou sur les critères d'exclusion (QI<80 ou 90).
- Elle touche autant les filles que les garçons.
Symptômes possibles
- Difficultés fréquentes en arithmétique, confusion entre les signes : +, -, /, ÷ et ×, difficultés avec les tables de multiplication, de soustraction, d’addition, de division, en calcul mental, etc.
- Difficultés dans les tâches quotidiennes comme vérifier sa monnaie et lire l’heure sur une montre analogique.
- Incapacité à comprendre une planification financière ou budgétaire, parfois même au niveau le plus basique, comme pour estimer le montant total d’un panier d’articles ou faire la balance de ses comptes.
- Peut être assez bon dans des matières comme la physique ou la géométrie, qui exigent de la logique plutôt que des formules, jusqu’au moment où il faut faire des calculs.
- Difficultés à comprendre le concept du temps et à estimer le temps qui passe. Peut être souvent en retard ou en avance.
- Problèmes spécifiques à distinguer sa droite de sa gauche.
- Peut être très bon dans le domaine de l’écriture. De nombreux auteurs et journalistes vivent avec ce trouble.
- Difficultés à naviguer ou à « tourner » mentalement la carte pour suivre la direction actuelle plutôt que l’usage habituel où le nord est en-haut.
- Peut avoir certaines difficultés à estimer mentalement les dimensions d’un objet ou une distance (par exemple, si quelque chose est entre 3 et 6 mètres de distance).
- Souvent incapable de saisir ou de se rappeler les concepts, règles, formules ou raisonnements mathématiques malgré de nombreuses révisions.
- Difficulté à lire un plan détaillé d'un objet à monter ou à construire soi-même.
- Incapacité à lire une suite de nombres, ou peut l’inverser lorsqu'il le répète, comme de dire 56 au lieu de 65.
- Incapacité à se remémorer les numéros de téléphone sans inverser des chiffres. Peut souvent s'y reprendre à plusieurs fois avant d'arriver à composer un numéro de téléphone dans l'ordre correct.
- Difficulté à remplir un chèque en raison de l'ordre imposé et doit souvent s'y reprendre une ou plusieurs fois.
- Difficulté à écrire avec exactitude, sur un cahier ou une feuille, une formule mathématique écrite sur un tableau, ce qui peut causer des retards et une lenteur à l'école.
- Difficulté dans des domaines nécessitant un traitement séquentiel. Du niveau concret (comme des pas de danse ou un autre sport) au niveau abstrait (énoncer les choses dans le bon ordre). Ils peuvent avoir aussi des difficultés même avec une calculatrice à cause de difficultés dans le processus de saisie de l'expression mathématique.
- La dyscalculie peut conduire dans des cas extrêmes à une phobie ou une angoisse durable des mathématiques et de ce qui y est lié.
- La dyscalculie peut angoisser car la notion du temps est assez erronée.
- Problèmes avec les grands nombres, les unités, dizaines, centaines…
- Faible inhibition latente, autrement dit plus de sensibilité aux bruits, aux odeurs, à la lumière et incapacité à faire la sourde oreille, à filtrer les informations et impressions non désirées. Peut avoir une imagination très développée à cause de cela (peut-être à titre de compensation cognitive de la déficience en calcul).
- Difficultés fréquentes de calcul de notes ou de moyennes lors de résultats scolaires.
Traitements
Il existe peu d'études rapportant les effets d'interventions auprès d'enfants dyscalculiques. Trundley[23] (1998) étudia l’impact d’interventions individuelles auprès d’enfants en difficulté en arithmétique. À raison d’une séance individuelle de vingt minutes par semaine, le professeur renforçait leurs habiletés de comptage, faisait réviser les faits arithmétiques déjà connus aux enfants en difficulté. Après cinq mois, il observa une augmentation importante du nombre de faits arithmétiques connus et une diversification des procédures de comptage.
Des programmes individuels s'adressant à des enfants dyscalculiques ont été testés avec succès en Australie (Wrigth et al. 2000, 2002) et en Angleterre (Dowker, 2001). Ces programmes, qui focalisent leur action sur les aspects des activités numériques les plus déficitaires des enfants, se sont avérés efficaces[6].
Un logiciel gratuit destiné à atténuer la dyscalculie a été développé par l’INSERM-CEA[24]. Il s'agit d'entraîner les enfants avec des tâches répétitives, présentées dans un cadre ludique et gratifiant. Une évaluation de ce logiciel de rééducation a été menée auprès de neuf enfants dyscalculiques qui s'exerçaient à raison d'une demi-heure par jour pendant cinq semaines. Les enfants ont amélioré leurs performances dans les tâches numériques de subitisation, de comparaison de chiffres, de nuages de points et dans la soustraction (A. Wilson[25], 2005).
Aides pédagogiques
Problématique
La dyscalculie est un trouble des apprentissages impliquant des difficultés dans l’intégration des notions de base en mathématiques, dans la production et la compréhension de raisonnements et dans les aptitudes arithmétiques. Ce retard dans la compréhension de ces notions, évalué par des tests standardisés, se manifeste par des résultats nettement en dessous du niveau escompté compte tenu de l’âge du sujet.
Ce trouble des apprentissages est de plus en plus courant mais malheureusement, les recherches liées sont peu nombreuses. Bon nombre d’acteurs de l’enseignement, ainsi que les parents, ne sont que trop peu au courant du sujet. Cela peut les placer dans des situations brumeuses face aux problèmes de l’enfant. Ils vont dès lors se perdre sur Internet afin de trouver des réponses à leurs inquiétudes. Il n’existe cependant pas beaucoup d’aides ciblées pour la dyscalculie.
Objectifs
La dyscalculie affecte un grand nombre de facultés liées aux mathématiques. Des problèmes apparaissent en algèbre comme en géométrie. Afin de proposer un travail de qualité, l'objectif ici est de remédier aux lacunes liées à l’addition et à la soustraction des nombres naturels. Voici les différentes compétences liées à ce sujet, tirées des Socles de Compétences [26](Ministère de la Fédération Wallonie-Bruxelles, 2013) :
- Identifier et effectuer des opérations d’addition et de soustraction dans des situations variées ;
- Utiliser, dans leur contexte, les termes usuels et les notations propres aux nombres et aux opérations d’addition et de soustraction ;
- Effectuer un calcul travaillant l’addition et la soustraction.
Les moyens numériques et leur(s) utilisation(s)
Pour les élèves
Le tableau blanc interactif (TBI)
Un premier moyen pour travailler les mathématiques avec le numérique est l’usage du tableau blanc interactif (TBI) qui se retrouve maintenant dans beaucoup de classes. Voici un exemple de son utilisation proposé par Lecocq[27] (2015).
Objectif : faire apparaitre deux cartes et demander aux apprenants de donner le résultat de la somme ou de la différence grâce au système des conteneurs. Ce système permet de faire glisser des objets dans des formes qui sont appelées « conteneurs ». On attribue des propriétés aux conteneurs afin qu’ils acceptent ou non des réponses.
Exemple :
Il y a deux cartes : la carte 3 et la carte 2. On demande la somme de ces deux cartes. L’élève doit faire glisser un des nombres sous les cartes dans le conteneur. Si sa réponse est correcte, le nombre va rester dans le conteneur, sinon, il sera éjecté.
La tâche peut être transformée en demandant aux élèves de placer un nombre de billes dans le conteneur. Cela permet également de faire varier les représentations d’un même nombre et de faire manipuler les élèves.
Scénario pédagogique envisageable :
Les formalités ont été créées pour convenir à des personnes dyscalculiques.
Objectifs du scénario :
- Savoir passer de la représentation sous forme de point à l’écriture numérique.
- Pouvoir compter en utilisant uniquement les chiffres numériques.
Étape 1 : la découverte de l’écriture numérique
L’enseignant projette au TBI la représentation des nombres sous forme de points. Les élèves viennent pour faire glisser les points dans le conteneur. L’enseignant travaille ensuite avec les élèves pour leur apprendre à passer de la représentation sous forme de points à la représentation numérique. Pour ce faire, elle utilise un référentiel, comme les dominos pour montrer la valeur des points du domino. Elle les utilise avec le TBI et demande à un élève de venir écrire la valeur équivalente. Exemple: un domino avec 5 points = 5.
Étape 2 : entraînement à l’écriture numérique
Les élèves ne disposent que des représentations numériques. Ils doivent réaliser le calcul en glissant la bonne réponse dans le conteneur. Si les élèves n’y arrive pas, l’enseignant peut revenir à l’étape 1. Si la représentation sous forme de points ne fonctionne toujours pas, l’enseignant distribue un matériel que les élèves peuvent manipuler avec leurs mains (exemple: des bonbons).
Évaluation envisageable :
Évaluation individuelle orale : chacun à leur tour, les élèves vont devant le TBI avec l’enseignant. Il propose de réaliser 5 calculs. Si ceux-ci sont réussis à 80%, l’objectif est atteint. S’il est entre 50% et 80%, l’enseignant vérifie que la représentation avec les formes est acquise. Si ce n’est pas le cas, il faut revoir la matière avec lui.
Pendant cette évaluation, les autres élèves sont occupés avec une autre activité pour ne pas déranger l’élève qui passe au TBI.
L’évaluation est la même pour tous les élèves, qu’ils soient dyscalculiques ou non, bien que les formalités aient été créées pour convenir à des personnes dyscalculiques.
La course aux nombres[28]
La course aux nombres est un jeu créé par l’Unité INSERM-CEA de Neuroimagerie Cognitive (centre de recherche en cognition mathématique). Il est adapté aux enfants de 4 à 8 ans, mais convient pour les plus âgés également. Il s’adresse tout particulièrement aux enfants dyscalculiques. En effet, le jeu permet de renforcer les circuits cérébraux de représentation et de manipulation des nombres. Il permet de découvrir les concepts de base des nombres et de l’arithmétique.
Il y a deux coffres comprenant des pièces ou des formes additives. Il faut choisir celui qui a le plus de pièces et faire avancer deux pions sur une ligne en fonction du nombre de pièces des coffres.
Notions travaillées :
- Comptage : entraînement avec les nombres de 1 à 40 ;
- Calculs élémentaires : additions et soustractions ;
- Présentation des nombres (ensembles concrets : chiffres ou mots).
Scénarios pédagogiques envisageables :
Les formalités ont été créées pour convenir à des personnes dyscalculiques.
Objectifs des scénarios :
- S’entraîner à reconnaître les nombres de 1 à 40.
- Additionner et soustraire avec ces nombres.
Avant même d’utiliser cette application, il est nécessaire que l’enseignant connaisse le niveau de ses élèves afin de les diriger vers les différents niveaux de difficulté : facile, intermédiaire, difficile.
Utilisation 1 : entraînement à domicile
L’enseignant commence par expliquer comment utiliser l’application et comment fonctionne celle-ci. Dans un principe de classe inversée, les élèves sont amenés à d’abord s’entraîner chez eux. L’application (gratuite) est disponible pour smartphones, PC et tablettes. Les élèves n’auront donc pas de mal à l’utiliser à la maison. Ils découvrent l’application et reviennent en classe avec 2,3 questions concernant leur utilisation de l’outil (exemple : pourquoi me suis-je trompé à telle question?).
En classe, l’enseignant répond aux questions des élèves et peut réexpliquer comment réaliser les exercices.
Utilisation 2 : remédiation pour ceux qui ont des lacunes
Les élèves passent d’abord un test diagnostic pour voir s’ils maitrisent les compétences travaillées par l’application. S’ils ne les maitrisent pas, ils utilisent l’application pour revoir leurs notions.
Utilisation 3 : entraînement en classe
L’enseignant crée des groupes de deux élèves (un élève plus faible, un élève plus fort). Par deux, ils utilisent l’application sur un ordinateur. L’élève plus fort doit guider le plus faible. Ils réalisent les exercices proposés par l’application. L’enseignant projette les exercices sur le TBI étant donné que cette application est utilisable avec celui-ci.
Évaluation envisageable :
L’évaluation est formative et ne sert qu’à savoir si l’élève a toujours besoin du jeu pour s’entraîner ou non. Pour évaluer l’atteinte des objectifs, une interrogation individuelle est nécessaire. Elle permet également de savoir si l’élève a compris la matière ou s’il a juste réussi les objectifs du jeu par essais-erreurs, et donc avec un facteur chance.
L'attrape nombres[29]
L’attrape nombres est un jeu créé par l’Unité INSERM-CEA de Neuroimagerie Cognitive (centre de recherche en cognition mathématique). Il est adapté aux enfants de 5 à 10 ans, mais convient pour les plus âgés également. Il s’adresse tout particulièrement aux enfants dyscalculiques. En effet, le jeu permet de renforcer les circuits cérébraux de représentation et de manipulation des nombres.
Des briques tombent du ciel (comme dans Tétris), le joueur doit remplir des camions avec les briques correspondantes.
Notions travaillées :
- Principe de la base 10 et des nombres à deux chiffres ;
- Calculs élémentaires : additions et soustractions ;
- Présentation des nombres (ensembles concrets : chiffres ou mots).
Scénarios pédagogiques envisageables :
Les formalités ont été créées pour convenir à des personnes dyscalculiques.
Objectifs des scénarios :
- S’entraîner à reconnaître les nombres de 1 à 40.
- Additionner et soustraire avec ces nombres.
Avant même d’utiliser cette application, il est nécessaire que l’enseignant connaisse le niveau de ses élèves afin de les diriger vers les différents niveaux de difficulté : standard ou expert.
Utilisation 1 : entraînement à domicile
L’enseignant commence par expliquer comment utiliser l’application et comment fonctionne celle-ci . Dans un principe de classe inversée, les élèves sont amenés à d’abord s’entraîner chez eux. L’application (gratuite) est disponible pour smartphones, PC et tablettes. Les élèves n’auront donc pas de mal à l’utiliser à la maison. Ils découvrent l’application et reviennent en classe avec 2,3 questions concernant leur utilisation de l’outil (exemple : pourquoi me suis-je trompé à telle question?).
En classe, l’enseignant répond aux questions des élèves et peut réexpliquer comment réaliser les exercices.
Utilisation 2 : remédiation pour ceux qui ont des lacunes
Les élèves passent d’abord un test diagnostic pour voir s’ils maitrisent les compétences travaillées par l’application. S’ils ne les maitrisent pas, ils utilisent l’application pour revoir leurs notions.
Utilisation 3 : entraînement en classe
L’enseignant crée des groupes de deux élèves (un élève plus faible, un élève plus fort). Par deux, ils utilisent l’application sur un ordinateur. L’élève plus fort doit guider le plus faible. Ils réalisent les exercices proposés par l’application. L’enseignant projette les exercices sur le TBI étant donné que cette application est utilisable avec celui-ci.
Évaluation envisageable :
L’évaluation est formative et ne sert qu’à savoir si l’élève a toujours besoin du jeu pour s’entraîner ou non. Pour évaluer l’atteinte des objectifs, une interrogation individuelle est nécessaire. Elle permet également de savoir si l’élève a compris la matière ou s’il a juste réussi les objectifs du jeu par essais-erreurs, et donc avec un facteur chance.
Math Kids
Math Kids est un jeu d'apprentissage gratuit conçu pour apprendre aux jeunes enfants les nombres et les mathématiques et disponible sur le Play Store et le Google Play. Il comporte plusieurs mini-jeux que les tout-petits et les enfants ayant des problèmes en calcul (addition et soustraction) peuvent employer. Math Kids aide à apprendre à identifier les nombres et à commencer à s'entraîner avec des énigmes d'addition et de soustraction. A la fin des jeux, il leur sera même possible de gagner des autocollants.
Les activités sont variées. L'application propose en effet des jeux variés :
- Comptage ;
- Puzzle addiction : remplir l’addition par les choix proposés ;
- Jeu d'addition : compter les objets résultant de l’addition ;
- Questionnaire d'addition : exercices d’addition (des choix sont disponibles) ;
- Comparer des groupes d'objets ;
- Puzzle soustraction : remplir la soustraction par les choix proposés ;
- Jeu de soustraction : compter les objets résultant de la soustraction ;
- Questionnaire de soustraction : exercices de soustraction (des choix sont disponibles).
Math Kids propose également certaines fonctionnalités permettant d’aider les adultes à contrôler et à gérer la progression de leurs enfants. Il est d'ailleurs possible d’augmenter ou de diminuer la difficulté, ou consulter les scores des activités précédentes.
Scénarios pédagogiques envisageables :
Les formalités ont été créées pour convenir à des personnes dyscalculiques.
Objectifs des scénarios :
- S’entraîner à reconnaître les nombres de 1 à 10 ;
- Compter des objets et associer un chiffre à cette quantité ;
- S’entraîner à composer la structure d’une addition et d’une soustraction;
- Additionner et soustraire avec ces nombres.
Utilisation 1: entraînement à domicile
L’enseignant commence par expliquer comment utiliser l’application et comment fonctionne celle-ci . L’application est assez intuitive et guide les utilisateurs en simulant une réponse lorsque c’est la première fois que l’on joue. Dans un principe de classe inversée, les élèves sont amenés à d’abord s’entraîner chez eux. L’application (gratuite) est disponible pour smartphones, PC et tablettes. Les élèves n’auront donc pas de mal à l’utiliser à la maison.
Pour chaque exercice, des choix sont à chaque fois proposés afin de mieux les guider. Pendant les différents jeux, l’utilisateur peut entendre le nom du nombre sur lequel il appuie ainsi que la réponse. Aucun feedback d’erreur n’est présent. La réponse est seulement non acceptée. Lorsque la réponse est correcte, elle est répétée par l’avatar, un message motivant est proposé et des autocollants sont parfois proposés.
Ils découvrent l’application et reviennent en classe avec 2,3 questions concernant leur utilisation de l’outil (exemple : pourquoi me suis-je trompé à telle question?).
En classe, l’enseignant répond aux questions des élèves et réexplique comment réaliser les exercices.
Utilisation 2: remédiation pour ceux qui ont des lacunes
Les élèves passent d’abord un test diagnostic pour voir s’ils maitrisent les compétences travaillées par l’application. S’ils ne les maitrisent pas, ils utilisent l’application pour revoir leurs notions.
Évaluations envisageables :
L’évaluation est formative et ne sert qu’à savoir si l’élève a toujours besoin du jeu pour s’entraîner ou non. Pour évaluer l’atteinte des objectifs, une interrogation individuelle est nécessaire. Elle permet également de savoir si l’élève a compris la matière ou s’il a juste réussi les objectifs du jeu par essais-erreurs, et donc avec un facteur chance. Durant l’évaluation, l’interface de l’application est utilisée. Par exemple, des objets seront donc présents accompagnant les exercices d’addition et de soustraction.
HP Reveal (réalité virtuelle)[30]
Cette application permet d’ajouter des informations supplémentaires aux élèves grâce à la réalité virtuelle. En effet, le professeur commence par prendre l’image d’un objet en photo. Ensuite, il lie cette image soit à un objet en mouvement, soit à une information (comme un lien Internet, par exemple). Enfin, quand l’élève utilise l’application avec un smartphone ou une tablette, il peut passer la caméra au-dessus de l’image et voir apparaitre les informations liées à cette dernière.
Scénario pédagogique envisageable :
Les formalités ont été créées pour convenir à des personnes dyscalculiques.
Objectif du scénario :
- Découvrir l’écriture numérique.
La découverte de l’écriture numérique
L’enseignant distribue des feuilles sur lesquelles se trouvent des calculs sous la forme numérique à résoudre. Il y a cinq additions et cinq soustractions. Exemples: 4+5= …. ou encore 5-4 = …
Les élèves seront installés deux par deux (pour favoriser la collaboration) et disposeront d’une tablette par groupe avec l’application.
Les élèves pourront passer la tablette au-dessus de leurs calculs et, de là, apparaitra la représentation sous forme de points du même calcul. Cela permettra aux élèves de répondre aux calculs plus facilement et d’acquérir la représentation numérique.
Évaluations envisageables :
L’application permet également de réaliser une évaluation formative avec des feedbacks.
Pour cela, l’enseignant crée une série d’additions et de soustractions sous format papier à compléter à l’aide de nombres munis de scratch. Le but est d’aider l’élève en lui proposant des feedbacks personnalisés et adaptés à l’erreur.
Chaque élève doit compléter les réponses aux calculs à l’aide de nombres munis de scratchs pour que, lorsque l’enfant passera la tablette au-dessus de son opération, la tablette reconnaisse sa solution. L’enseignant organise deux sortes de feedback : lorsque la réponse est bonne et quand elle ne l’est pas.
En cas de bonne réponse, la tablette donne, en réalité virtuelle, un petit bonhomme content. Dans l’autre cas, elle envoie une explication supplémentaire pour que l’élève puisse comprendre son erreur. Pour cela, l’enseignant doit penser à l’avance aux types d’erreurs possibles pour les enfants. De cette manière, le feedback est spécifique à leur erreur.
Pour les enseignants
Le cartable fantastique[31]
Ce site Internet permet aux enseignants d’aider les élèves ayant des troubles de l’apprentissage dans la réalisation de tâches en classe grâce à une boîte à outils. Dans l'accueil, la dyspraxie est principalement présentée. Certaines notions sont compatibles avec la dyscalculie (voir glossaire). Les enseignants peuvent donc utiliser la boîte à outil, sans oublier de filtrer les informations en fonction des besoins de l’élève.
Il propose différents outils : ceux pour « compenser » ainsi que ceux pour « adapter ». L’enseignant peut choisir s’il souhaite différencier son contenu ou aider l’élève à compenser ses difficultés en classe. Une fois le type d’outils choisi, l’enseignant peut prendre la compétence qu’il va travailler avec les élèves. Par exemple : lire, compter, conjuguer… Ce site permet donc d’aider les professeurs de mathématiques, mais également les autres professeurs. Les difficultés de l’enfant sont présentes, peu importe le cours.
Pour chaque outil, le Cartable Fantastique explique aux enseignants comment l’utiliser et donne accès au téléchargement des différents logiciels.
Ce qui est également intéressant, c’est que le site propose pour chaque partie « Des petits trucs » en plus permettant de compléter les astuces, ainsi que d’aides proposés par des enseignants ayant également utilisés l’outil (« l’astuce de … »).
Pour finir, le Cartable Fantastique propose des exercices numériques en ligne « tout faits » pour entraîner l’enfant sur certaines notions plus difficiles, ainsi que des cahiers adaptés à télécharger pour les enfants. Cette partie est créée tant pour les cours de mathématiques que pour les cours de français, de sciences
Pour ces exercices, il propose au préalable à l’enfant des aides dans les boîtes à outils.
Scénarios pédagogiques envisageables :
Les formalités ont été créées pour convenir à des personnes dyscalculiques. L’outil propose aux enseignants des scénarios pédagogiques.
Une méthode sur la mémoire émotionnelle
Les Innombrables
Cette méthode est basée sur le constat que pour faciliter les apprentissages, il faut un contexte ou un environnement apaisant pour l'élève et un attrait, une curiosité pour les mathématiques sans quoi les capacités cognitives ne seront pas optimisées.
La méthode propose la découverte d'un univers ou les personnages sont des nombres. L'enfant les identifie grâce à leur couleur ou à leur caractère, c'est là que l'affectif entre en jeu. Il mémorisera ainsi parfois de manière spectaculaire les compléments à 10 ou les doubles qui pouvaient être difficilement accessibles pour certains élèves affectés par des troubles d'apprentissage ou bloqués par le côté abstrait des premières notions mathématiques.
Les livres sont complétés par d'autres outils pédagogiques (comme le jeu de cartes de la classification) ou l'enfant est même autorisé à tricher afin de pouvoir compléter ses familles de nombres. En se rappelant les histoires, et en jouant avec les nombres, il se crée ainsi ses propres repères via sa mémoire émotionnelle et sa mémoire épisodique. La méthode permet d'autres outils à la disposition des parents et des enseignants et son application est compatible avec la MHM ou d'autres méthodologie d'apprentissage classiques.
Vidéo intéressante
La vidéo Dyscalculie apprendre à compter et calculer : Jeu Au bout du compte ! (2012).[32]
Plusieurs jeux et matériels existent afin d’aider les enfants ayant une dyscalculie ou des problèmes de compréhension des mathématiques.
Une logopède propose l’outil Au bout du compte. Dans sa vidéo sur YouTube, elle détaille en dix minutes le matériel en expliquant son utilité et son fonctionnement. Un cas pratique est mis en œuvre afin de mieux cerner la façon de travailler avec l’outil.
La difficulté principalement travaillée par le jeu est le calcul mental. Un enfant présentant une dyscalculie ou des difficultés à réaliser des opérations peut tenter de remédier à ses lacunes. Il propose de travailler les habiletés numériques et les calculs élémentaires. L’utilisation est prévue pour les enfants en maternelle jusqu'à la fin du primaire.
Grâce à ces activités, il est possible :
1. D'aborder et de contrôler les premiers principes additifs et soustractifs de l'enfant ;
2. De développer des procédures efficaces dans la réalisation d'un calcul réfléchi ;
3. D'être au plus près du potentiel cognitif de l'enfant en pratiquant un apprentissage contrôlé par l'anticipation mentale et par l'action effective.
Durant l'activité, nous serons amenés à utiliser des cartes bifaces (recto verso) permettant le développement de la mémoire de travail et l’organisation d'une bonne commutativité de l'opération d'addition. Par exemple, le fait de calculer en partant de la quantité au recto ou en partant de la quantité au verso.
Au bout du compte est composé :
- d'un livret explicatif ;
- de six activités de calcul sous forme de jeux de cartes :
Activité 1 : CARTES BIFACES (double constellation de points)
Activité 2 : CARTES BIFACES (constellation de points / numéral arabe)
Activité 4 : CARTES BIFACES (double / moitié)
Activité 3 : CARTES BIFACES (numéral arabe / numéral arabe)
Activité 5 : DOMINOMBRES n° 1 (même chiffre)
Activité 6 : DOMINOMBRES n° 2 (compléments de dix).
Scénarios pédagogiques envisageables :
Les formalités ont été créées pour convenir à des personnes dyscalculiques.
L’outil propose aux enseignants des scénarios pédagogiques.
Des ressources supplémentaires
APEDA [33]
Voici une note explicative de l’APEDA concernant leur projet : Modèle:Ciation
Cognifit
Voici un test en ligne[34] pour savoir si un individu est dyscalculique.
Plusieurs tests sont réalisables afin de déceler ou non ce trouble. La plupart ne sont bien entendu pas disponibles sur Internet ou une contribution est demandée pour y accéder. Ceux-ci ne sont pas pour autant « officiels » et sont encore à améliorer.
Sur le site de Cognifit (2017), un groupe d'experts en psychologie et en neuropsychologie met à la disposition des usagers un test en neuf parties. La batterie de tests prend 15-20 minutes à réaliser et est destinée aux enfants (six ans et plus) ainsi qu’aux adultes.
Ce dernier est composé de plusieurs tests courts. Chacun à sa manière permet de détecter deux ou plusieurs symptômes de la dyscalculie. Ils ne travaillent donc pas sur la dyscalculie elle-même mais sur les indices antérieurs. Un déficit cognitif pourra être repéré à la suite de cela. L’utilisateur recevra une conclusion sous forme de tableaux et graphiques mettant en avant les capacités intellectuelles défaillantes.
Voici les différentes compétences exploitées :
• Domaine de la Mémoire : mémoire de travail et mémoire à court terme.
• Domaine de l'Attention : concentration, attention partagée et dénomination.
• Domaine de la Perception : reconnaissance.
• Domaine de la Coordination : temps de réaction.
• Domaine du Raisonnement : planification et vitesse de traitement.
Dys-Positif [35]
Voici une note explicative des auteurs du site Dys-Positif concernant les astuces qu’ils ont partagées : « Les mathématiques sont l’une des matières qui importent le plus au primaire et au secondaire. Matière décisive, c’est elle qui pèse le plus sur le bulletin scolaire, mais c’est également elle qui motive le choix de l’orientation ! Voilà pourquoi, ne pas rater les maths est crucial ! Et voilà pourquoi, la situation de l’enfant qui souffre de la dyscalculie est délicate.
Souffrant d’un déficit au niveau de l’acquisition des notions de nombre et du calcul, le dyscalculique est tout simplement incapable d’acquérir et de maitriser toute connaissance qui touche aux mathématiques. Il en résulte des notes souvent catastrophiques, qui ne semblent pas s’améliorer malgré la persévérance de l’enseignant.
Votre enfant souffre de dyscalculie ? Pour aider votre enfant à surmonter son handicap, vous l’avez certainement déjà compris, vous devez mettre la main à la pâte ! Révision, exercice… est à faire à la maison pour compenser le trouble. Oui, mais comment faire ? Nous vous proposons quelques astuces pour l’aider dans ses devoirs… »
Conférence Jacinthe Giroux [36]
Voici une vidéo que l’on peut retrouver sur Vimeo. Elle a été publiée par La Haute école pédagogique du canton de Vaud (2015) : Modèle:Ciation. Celle-ci explicite également les apports de la didactique pour les élèves en difficulté en mathématiques
L’inclusion scolaire [37]
Voici une page du site Enseignement.be qui définit ce qu’est l’inclusion scolaire, qui explique comment la mettre en place et qui propose une typologie des aménagements raisonnables et des fiches outils sur ces aménagements. Au total, deouze fiches sont disponibles. Elles reprennent les aménagements raisonnables possibles pour les troubles suivants : bégaiement, daltonisme, dyscalculie, dysgraphie, dyslexie, dysorthographie, dysphasie, dyspraxie, Haut Potentiel Intellectuel (HPI), syndrome d’Asperger, syndrome dysexécutif, trouble de l’attention avec/sans hyperactivité (TDA/H). Elles sont téléchargeables via un fichier .zip.
Notes et références
- ↑ L’agnosie digitale est l'incapacité à reconnaître, identifier, différencier, nommer, sélectionner et orienter les doigts individuellement sur ses propres mains et celles d’autrui.
Références
- ↑ Anatole Bailly, Abrégé du dictionnaire grec–français, Paris, Librairie Hachette, c. 1925, 12e éd. (1re éd. 1901), XII–1012 p., in-8o (245 × 155 mm) (ISBN 978-2-01-003528-9, lire en ligne [flash]).
- ↑ (en) David Pollak, Neurodiversity in higher education : positive responses to specific learning differences, Chichester, John Wiley and Sons, , 1re éd., 322 p., poche (ISBN 978-0-470-99753-6, LCCN 2008052047, lire en ligne), p. 125–.
- ↑ (en) Ladislav Kosc, « Developmental dyscalculia », Journal of Learning Disabilities, Hammill Institute on Disabilities, vol. 7, no 3, , p. 164–177 (ISSN 0022-2194 et 1538-4780, DOI 10.1177/002221947400700309, résumé).
- 1 2 3 4 S. Dehaene, N. Molko et A. Wilson, « Dyscalculie, le sens perdu des nombres », La Recherche, Paris, vol. 379, (ISSN 0029-5671).
- ↑ (en) American Psychiatric Association, « Diagnostic and statistical manuel of mental disorders dsm-iv », American Psychiatric Pub, .
- 1 2 3 4 Expertise collective, « Dyslexie, Dysorthographie, Dyscalculie : Bilan des données scientifiques »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) [PDF], sur medias.formiris.org, Les éditions INSERM, .
- ↑ (en) D. C. Geary, S. C. Brown et Samaranayake, « Cognitive addition: A short longitudinal study of strategy choice and speed-of-processing differences in normal and mathematically disabled children », Developmental Psychology, vol. 27, no 5, .
- ↑ (en) N. C. Jordan et T. O. Montani, « Cognitive arithmetic and problem solving: A comparison of children with specific and general mathematics difficulties », Journal of Learning Disabilities, vol. 30, , p. 624–634 (ISSN 0022-2194 et 1538-4780).
- ↑ (en) B. P. Rourke et J. A. Conway, « Disabilities of arithmetic and mathematical reasoning: Perspectives from neurology and neuropsychology », Journal of Learning Disabilities, vol. 30, no 1, , p. 34–46 (ISSN 0022-2194 et 1538-4780).
- ↑ (en) D. C. Geary, « Mathematics and learning disabilities », Journal of Learning Disabilities, vol. 37, no 1, , p. 4-15 (ISSN 0022-2194 et 1538-4780).
- ↑ (en) M. von Aster, « Developmental cognitive neuropsychology of number processing and calculations: Varieties of developmental dyscalculia », European Child & Adolescent Psychiatry, vol. 9, .
- ↑ (en) M. Alarcon, J. Defries et Pennington B. Gillis, « A twin study of mathematics disability », J. of Learning Disabilities, vol. 330, , p. 617–623 (ISSN 0022-2194 et 1538-4780).
- ↑ Stanislas Dehaene, La Bosse des maths, Éditions Odile Jacob, 1977, 2003.
- 1 2 3 (en) Anna J. Wilson et Stanislas Dehaene (édition par Coch, Dawson et Fischer), « Number Sense and Developmental Dyscalculia », Human Behavior, Learning, and Developing Brain: Atypical Development, Guilford Press, .
- ↑ (en) A. Nieder et E. K. Miller, « A parieto-frontal network for visual numerical information in the monkey », Proc Natl Acad Sci U S A, vol. 101, no 19, .
- ↑ (en) Véronique Izard, Ghislaine Dehaene-Lambertz, Stanislas Dehaene et al., « Distinct Cerebral Pathways for Object Identity and Number in Human Infants », PLoS Biol, vol. 6, no 2, .
- ↑ (en) L. M. Levy, I. L. Reis et J. Grafman, « Metabolic abnormalities detected by 1H-MRS in dyscalculia and dysgraphia », Neurology, vol. 53, , p. 639–641 (PMID 10449137, lire en ligne).
- ↑ (en) E. Mayer, M. D. Martory, A. Pegna, T. Landis, J. Delavelle et J. M. Annoni, « A pure case of Gerstmann syndrome with a subangular lesion », Brain, vol. 122, , p. 1107–1120 (PMID 10356063, lire en ligne).
- ↑ (en) J. W. Adams et G. J. Hitch, « Working memory and children's mental addition », J Exp Child Psychol, vol. 67, no 1, , p. 21–38 (PMID 9344485, DOI 10.1006/jecp.1997.2397, lire en ligne, consulté le ).
- ↑ (en) Geary D. C., « Mathematical disabilities: cognitive, neuropsychological, and genetic components », Psychol Bull, vol. 114, , p. 345–362 (PMID 8416036, lire en ligne).
- ↑ (en) M. C. Monuteaux, S. V. Faraone, K. Herzig, N. Navsaria et J. Biederman, « ADHD and dyscalculia: Evidence for independent familial transmission », J Learn Disabil, vol. 38, no 1, , p. 86–93 (ISSN 0022-2194 et 1538-4780, PMID 15727331, lire en ligne).
- ↑ (en) O. Rubinsten et A. Henik, « Developmental dyscalculia: heterogeneity might not mean different mechanisms », Trends Cogn. Sci. (Regul. Ed.), vol. 13, no 2, , p. 92–99 (PMID 19138550, DOI 10.1016/j.tics.2008.11.002, lire en ligne).
- ↑ (en) R. Trundley, « The Devon Raising Attainment in Numeracy Project, 1997–1998 : Final Report », Devon Curriculum Services, .
- ↑ (en) A. J. Wilson, S. K. Revkin, D. Cohen, L. Cohen et S. Dehaene, « An open trial assessment of "The Number Race", an adaptive computer game for remediation of dyscalculia », Behav Brain Funct, vol. 2, , p. 20 (ISSN 1744-9081, PMID 16734906, PMCID 1523349, DOI 10.1186/1744-9081-2-20, lire en ligne, consulté le ).
- ↑ Anna Wilson, « Dyscalculie développementale : l’approche « neurocognitive » », Fondation Fyssen, Annales, vol. 20, .
- ↑ Ministère de la Fédération Wallonie-Bruxelles. (2013). Socles de compétences. Enseignement fondamental et premier degré de l’enseignement secondaire. Enseignement de la communauté française, Administration Générale de l’Enseignement et de la Recherche scientifique, Service général des Affaires pédagogiques, de la Recherche en Pédagogie et du Pilotage de l’Enseignement organisé par la communauté française.
- ↑ Lecocq, S. (2015). Dyscalculie. Consulté à l’adresse http://www.instit2.be/2015/10/11/dyscalculie/.
- ↑ « La course aux nombres – Un jeu qui enseigne l’arithmétique et combat la dyscalculie », sur www.lacourseauxnombres.com (consulté le )
- ↑ « L’Attrape-Nombres – Jouer », sur www.attrape-nombres.com (consulté le )
- ↑ « HP Reveal - HP Reveal », sur www.hpreveal.com (consulté le )
- ↑ Cartable fantastique. (2019). Une boîte à outils pour les élèves dyspraxiques. Consulté à l’adresse https://www.cartablefantastique.fr/
- ↑ Orthophonie94. (2012, 4 septembre). Dyscalculie apprendre à compter et calculer : Jeu Au bout du compte ! [Vidéo en ligne]. Consulté à l’adresse https://www.youtube.com/watch?v=xdDCHiQCLDA
- ↑ APEDA. (s.d.). Boîte à outils. Consulté à l’adresse https://www.apeda.be/aider/boite-outils/
- ↑ Cognifit. (s.d.). Test de dyscalculie en ligne (CAB-DC). Consulté à l’adresse https://www.cognifit.com/fr/cognitive-assessment/dyscalculia-test
- ↑ Dys-positif. (s.d.). La dyscalculie : quelques astuces pour les exercices. Consulté à l’adresse https://www.dys-positif.fr/la-dyscalculie-quelques-astuces-pour-les-exercices/
- ↑ Haute école pédagogique du canton de Vaud (HEP Vaud). (2015, 20 octobre). Conférence Jacinthe Giroux [Vidéo en ligne]. Consulté à l’adresse https://vimeo.com/143005163
- ↑ Fédération Wallonie-Bruxelles. (s.d.). L’inclusion scolaire. Consulté à l’adresse : http://enseignement.be/index.php?page=27775&navi=4312&rank_page=27775.
Voir aussi
Bibliographie
- Josiane Helayel et Isabelle Causse-Mergui, 100 idées pour aider les élèves dyscalculiques, éd., .
- (en) Samantha Abeel, My Thirteenth Winter : A Memoir, Orchard Books, , 203 p. (ISBN 0-439-33904-9).
- (en) Tony Attwood, Dyscalculia in Schools : What It Is and What You Can Do, First and Best in Education Ltd., , 140 p. (ISBN 1-86083-614-3).
- (en) Brian Butterworth, Dyscalculia Guidance : Helping Pupils With Specific Learning Difficulties in Maths, David Fulton Publications, (ISBN 0-7087-1152-9).
- (en) Steve Chinn, The Trouble with Maths : A Practical Guide to Helping Learners with Numeracy Difficulties, RoutledgeFalmer, (ISBN 0-415-32498-X).
- (en) Anne Henderson, Fil Came et Mel Brough, Working with Dyscalculia, Learning Works International Ltd., (ISBN 0-9531055-2-0, lire en ligne).
- (en) Mahesh Sharma, « Dyscalculia »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), sur www.bbc.co.uk, BBC, (consulté en ).
- (en) Mahesh Sharma et Eugene Loveless, « Dyscalculia », CT/LM « Focus on Learning Problems in Mathematics », .
- (en) Mahesh Sharma, « Dyslexia, Dyscalculia and other Mathematics Problems », CT/LM « The Math Notebook », .
- (en) Mahesh Sharma, « Berkshire mathematics »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), (consulté en ).
- (en) Jamie I. D. Campbell, Handbook of Mathematical Cognition, Psychology Press, .
Articles connexes
- Innumérisme
- Troubles « dys- »
- Difficultés en mathématiques
- Liste des troubles mentaux
Liens externes
- (fr + en + pl + sv) L’unité INSERM-CEA de NeuroImagerie Cognitive, « La course aux nombres : Comment fonctionne le logiciel — le contexte scientifique », sur www.lacourseauxnombres.com, (consulté le ).
- https://dyscalculieenmaternelle.jimdofree.com/