Ensemble de définition

En mathématiques, l'ensemble de définition (également appelé domaine de définition ou parfois ensemble de départ, voir la discussion plus bas) d'une application ou d'une fonction désigne informellement l'ensemble des entrées acceptées par elle.

Diagramme sagittal d'une fonction d'ensemble de définition

A

= {1,2,3,4} et d'ensemble d'arrivée

B

= {a,b,c,d}.

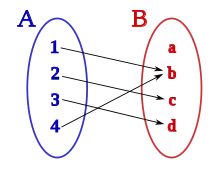
La terminologie entre ensemble de définition et ensemble de départ diffère si l'on fait la distinction entre la notion de fonction et d'application ou non^[1].

Pour une application $f : A \to B$ (ou pour une fonction si on ne fait pas cette distinction), les notions d'ensemble de définition et d'ensemble de départ sont confondues, il s'agit de l'ensemble $A$ , autrement dit c'est l'ensemble des $x$ pour lesquels $f (x)$ est défini.
Si on fait la distinction entre application et fonction, une fonction $f : A \to B$ peut ne pas être une application, son ensemble de définition, noté ici $D f$ , peut différer de son ensemble de départ $A$ . L'ensemble de définition $D f$ est alors l'ensemble des éléments $x$ de $A$ pour lesquels $f (x)$ est défini ; la différence avec les applications étant qu'il peut exister des $x$ de $A$ pour lesquels on ne définit pas $f (x)$ . Dans ce cas l'ensemble de définition $D f$ n'est pas égal à l'ensemble de départ $A$ .

Lorsque l'ensemble de définition est simplement un intervalle, l'ensemble de définition est parfois appelée intervalle de définition.

Exemple

Dans le cas où on distingue les notions de fonction et d'application, considérons

{\begin{array}{ccccc}f&:&\mathbb {R} &\to &\mathbb {R} \\&&x&\mapsto &{\frac {1}{x}}~.\end{array}}

C'est une fonction dont l'ensemble de départ est $\mathbb {R}$ . Cependant, son ensemble de définition $D_{f}$ ne peut pas être égale à l'ensemble de départ $\mathbb {R}$ puisqu'elle n'est pas définie en 0 : « $f (0)$ » n'est pas défini, car il est impossible de diviser par 0. Ce n'est donc pas une application.

Il faut donc préciser ici, pour définir complètement cette fonction, son ensemble de définition $D_{f}$ (ce qui n'est pas encore fait à ce stade). Il y a ici une infinité de choix possibles : tout sous-ensemble de l'ensemble de départ $\mathbb {R}$ ne contenant pas 0 convient. Un choix « naturel » est simplement $D_{f}=\mathbb {R} ^{*}=\mathbb {R} \setminus \{0\}$ .

Restriction et prolongement

Restriction pour une application

En partant d'une application $f : A \to B$ d'ensemble de définition A, il est toujours possible de construire une autre application en restreignant l'ensemble de définition. Si $E$ est un sous-ensemble de $A$ , alors

{\begin{array}{ccccc}f_{|E}&:&E&\to &B\\&&x&\mapsto &f(x)\end{array}}

définie une application appelée restriction de f à E. Son ensemble de définition (qui est aussi son ensemble de départ) est alors E.

Restriction pour une fonction

Pour une fonction $f : A \to B$ d'ensemble de départ $A$ et d'ensemble de définition $D f$ , deux opérations de restrictions sont possibles: restriction de l'ensemble de départ A ou restriction de l'ensemble de définition $D f$ .

On peut restreindre l'ensemble de définition $D f$ à un sous-ensemble de $D f$ . Par exemple, on peut considérer la fonction

{\begin{array}{ccccc}g:&\mathbb {R} &\to &\mathbb {R} \\&x&\mapsto &{\frac {1}{x}}\end{array}}

d'ensemble de définition

D_{g}=\;]0,+\infty [

qui est la restriction de la fonction

{\begin{array}{ccccc}f:&\mathbb {R} &\to &\mathbb {R} \\&x&\mapsto &{\frac {1}{x}}\end{array}}

d'ensemble de définition

D_{f}=\mathbb {R} ^{*}

On peut restreindre l'ensemble de départ $A$ à un sous-ensemble E de A comme on l'a fait pour les applications, dans ce cas il faut s'assurer que l'ensemble de définition de la nouvelle fonction est inclus dans E. Un choix naturel est de considérer l'intersection $E\cap D_{f}$ (mais tout sous-ensemble de cet ensemble conviendrait également).

L'un des intérêts de l'opération de restriction de l'ensemble de départ est qu'il est toujours possible de transformer une fonction $f : A \to B$ en application en restreignant son ensemble de départ à son ensemble de définition $D f$ en posant

{\begin{array}{ccccc}f_{|D_{f}}&:&D_{f}&\to &B\\&&x&\mapsto &f(x)\end{array}}

Cela définit une application. Par exemple, en reprenant l'exemple de la fonction

{\begin{array}{ccccc}f&:&\mathbb {R} &\to &\mathbb {R} \\&&x&\mapsto &{\frac {1}{x}}~.\end{array}}

d'ensemble de définition $D_{f}=\mathbb {R} ^{*}$ , poser

{\begin{array}{ccccc}f_{|\mathbb {R} ^{*}}:&\mathbb {R} ^{*}&\to &\mathbb {R} \\&x&\mapsto &{\frac {1}{x}}\end{array}}

définit une application.

Prolongement d'une fonction

Pour une fonction $f : A \to B$ d'ensemble de départ A et d'ensemble de définition $D f$ , on peut construire une application en définissant les valeurs de f(x) pour tous les x de A qui ne sont pas dans $D f$ (c'est-à-dire pour lesquelles f(x) n'est pas définie).

Par exemple, toujours en considérant

{\begin{array}{ccccc}f&:&\mathbb {R} &\to &\mathbb {R} \\&&x&\mapsto &{\frac {1}{x}}~.\end{array}}

d'ensemble de définition $D_{f}=\mathbb {R} ^{*}$ , on définit un prolongement en posant

{\begin{array}{ccccc}{\widetilde {f}}&:&\mathbb {R} &\to &\mathbb {R} \\&&x&\mapsto &\left\{{\begin{array}{ll}{\frac {1}{x}}~&(x\neq 0)\\0&(x=0)\end{array}}\right.\end{array}}

Cela définit une application. Le choix de la valeur ${\widetilde {f}}(0)=0$ est ici arbitraire, tout autre nombre réel aurait convenu.

Assez souvent, pour alléger les notations, le prolongement est noté de la même manière que la fonction initiale. Cette ambiguïté est sans conséquence si le prolongement est explicité et remplace aussitôt et définitivement la fonction initiale.

Notes et références

↑ Voir Application_(mathématiques)#Fonction_et_application pour plus de détails

Lien externe

« Théorie et exercices sur les domaines de définitions » [PDF], sur le site d'exercices, cours et annales de mathématiques pour économistes, de G. Carin et B. Dupont, université Lille I (version du 26 septembre 2007 sur Internet Archive)