Onde stationnaire résultant de la superposition d'ondes de sens inverse ; les points rouges sont les nœuds de vibration.

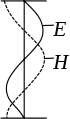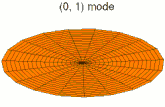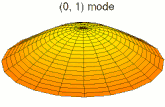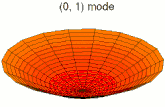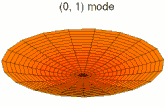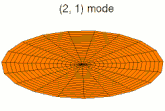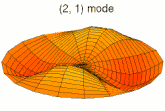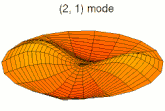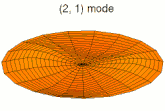
En physique ondulatoire, une onde stationnaire est une oscillation locale dans un milieu clos, qui ne se propage pas. On appelle les points où l'amplitude est nulle des nœuds de vibration, et ceux où l'amplitude est maximale des ventres de vibration.

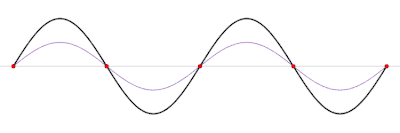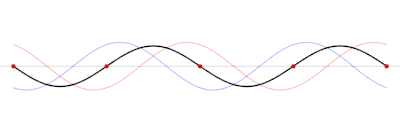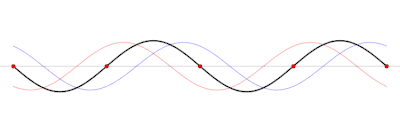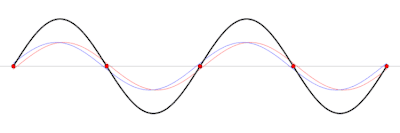
Dans un milieu à une dimension, comme un conducteur électrique ou un tuyau, elle est la résultante de la superposition d'ondes de même fréquence et de même amplitude mais de sens de propagation opposé (CIE).

Dans un milieu à plusieurs dimensions, comme une plaque ou un volume, les ondes stationnaires résultent de la superposition d'ondes dont la somme vectorielle est nulle, ce qui n'est possible que pour certaines longueurs d'onde^[1].

Détails

Selon le point observé, les vibrations produites par les différentes ondes s'additionnent ou se compensent de manière partielle ou totale, ce qui provoque à des emplacements définis et fixes leur neutralisation mutuelle (lieux appelés « nœuds » : les vibrations disparaissent) ou leur addition (lieux appelés « ventres » : les vibrations sont amplifiées et maximales). La distance séparant un nœud du nœud le plus proche est égale à la distance de la corde divisée par le nombre de ventres. Une onde stationnaire s'établit sur une corde dans le cas où :

ou, autrement dit,

avec ${\displaystyle L}$ la longueur de la corde, ${\displaystyle \lambda }$ la longueur de l'onde s'établissant dans la corde et ${\displaystyle n}$ le nombre de ventres.

Les fréquences pour lesquelles elles s'établissent s'appellent les modes harmoniques de vibration et dépendent de la corde et de la tension qui lui est appliquée et sont toutes multiples d'un entier et de la plus petite fréquence à laquelle la corde vibre. Soit : ${\displaystyle f_{n}=nf_{0}}$, avec ${\displaystyle f_{n}}$ la fréquence du mode harmonique de rang ${\displaystyle n}$, ${\displaystyle n}$ le rang de l'harmonique ${\displaystyle (n\in \mathbb {N} )}$ et ${\displaystyle f_{0}}$ la fréquence du mode fondamental de vibration de la corde.

Exemples

Les ondes stationnaires peuvent affecter tous les phénomènes vibratoires : mécaniques, sonores, optiques, électromagnétiques, etc. Elles peuvent être mises en évidence de nombreuses façons : cordes vibrantes, tube de Kundt, interférences sonores ou lumineuses, etc.

Les milieux affectés par des ondes stationnaires peuvent être à une, deux ou trois dimensions ; voici quelques exemples :

• une dimension
  • corde vibrante
  • tuyau sonore (en première approximation, d'autant meilleure que son diamètre est plus faible)
  • fibre optique
• deux dimensions :
  • table d'harmonie des instruments de musique
  • surface d'un plan d'eau (seiche) ou d'un réservoir de mercure
• trois dimensions
  • volume intérieur d'une église (vis-à-vis du son de l'orgue)
  • espace affecté par des interférences lumineuses, par exemple, une cavité optique

Annexes

Notes et références