Phase

L'oscillation d'un pendule est périodique vis-à-vis du temps ; la phase est alors une fonction du temps.

Données clés

Unités SI	1
Autres unités	radian (rad)
Dimension	${\displaystyle 1}$
Nature	Grandeur scalaire
Symbole usuel	${\displaystyle \mathrm {\phi } ,\Phi }$

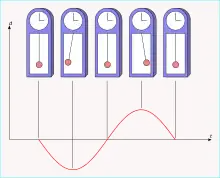
En physique, la phase d'une fonction périodique est l'argument de cette fonction, noté souvent ${\displaystyle \Phi }$. Elle est définie modulo la période, c'est-à-dire à un nombre entier de périodes près.

Par exemple, la hauteur d'un pendule oscillant est une fonction sinusoïdale de la forme ${\displaystyle f(t)=A\sin(\omega t+\alpha )}$. La phase ${\displaystyle \Phi }$ vérifie alors ${\displaystyle \Phi (t)=\omega t+\alpha }$ à ${\displaystyle 2\pi }$ près, avec ${\displaystyle \omega }$ la pulsation et ${\displaystyle \alpha }$ la phase initiale.

Présentation

Ondes sinusoïdales déphasées.

Ondes sinusoïdales en phase. Leur somme est constructive.

La phase est une grandeur sans dimension. Cependant, dans le cas d'un signal sinusoïdal, on attribue l'unité radian ou degré à la phase. En effet, on peut ramener le phénomène périodique à une rotation fictive sur le cercle unité et interpréter dans ce cas la phase en tant qu'angle.

Par abus, on attribue parfois une dimension de longueur ou de temps à la phase, ce qui en pratique ne change rien. Cela peut néanmoins engendrer des incohérences d'inhomogénéité dans un développement en série de la fonction périodique étudiée.

On étudie souvent la différence de phase entre deux signaux qui ont la même pulsation, qu'on nomme déphasage. Si ces signaux sont additifs, comme par exemples les ondes, alors les différences de phases sont responsables d'interférences.

Des signaux de même pulsations dont les phases sont identiques sont dits en phase, sinon ils sont dits déphasés. Des signaux dont les phases diffèrent d'une demi-période sont dits en opposition de phase. Pour des ondes, on parle d'interférences constructives ou destructives.

En complexe

Il est courant d'étudier un phénomène ondulatoire sous un formalisme complexe pour des raisons de facilités calculatoires qui n'apparaîtraient pas autrement.

Pour un signal sinusoïdal ${\displaystyle f}$, on associe une fonction exponentielle complexe ${\displaystyle S}$ de la forme :

${\displaystyle f(\Phi )=A\cos(\Phi )\ \ \longleftrightarrow \ \ Ae^{i\Phi }=S(\Phi )}$

L'argument de l'exponentielle vaut alors la phase du signal et peut être assimilé à un angle dans le plan complexe.

La phase correspond à l'angle ${\displaystyle \theta }$, et ${\displaystyle |z|}$ vaut la valeur absolue de A.

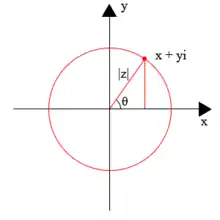
On peut géométriquement remonter à la phase avec les parties réelles et imaginaires ${\displaystyle \Re (S)}$ et ${\displaystyle \Im (S)}$ de la fonction complexe ${\displaystyle S}$ :

• Si ${\displaystyle \Re (S)}$ est positive, ${\displaystyle \Phi =\arctan \left({\frac {\Im (S)}{\Re (S)}}\right)}$ ;
• Si ${\displaystyle \Re (S)}$ est négative, ${\displaystyle \Phi =\arctan \left({\frac {\Im (S)}{\Re (S)}}\right)+\pi }$.

Une autre propriété intéressante du formalisme complexe est qu'il devient facile de modifier la phase du signal : il suffit de multiplier par ${\displaystyle e^{i\alpha }}$ le signal pour ajouter ${\displaystyle \alpha }$ à la phase. En effet :

${\displaystyle Ae^{i\Phi }\times e^{i\alpha }=Ae^{i(\Phi +\alpha )}\ \ \longleftrightarrow \ \ A\cos(\Phi +\alpha )}$

On retrouve cet emploi dans les diagrammes de Bode ; si ${\displaystyle H}$ la fonction de transfert vérifie ${\displaystyle H(\omega )=A(\omega )e^{-i\Phi (\omega )}}$ avec ${\displaystyle A}$ fonction réelle, alors pour un ${\displaystyle \omega }$ fixé, le signal de sortie est amplifié de ${\displaystyle A(\omega )}$ et déphasé de ${\displaystyle \Phi (\omega )}$.

Voir aussi