
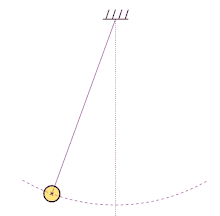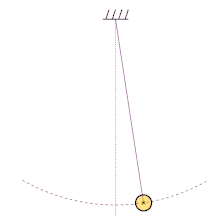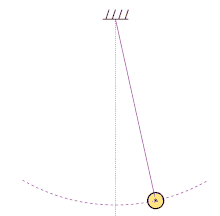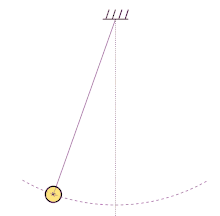
En physique, le pendule simple est une masse ponctuelle fixée à l'extrémité d'un fil sans masse et inextensible[1], et oscillant sous l'effet de la pesanteur. Il s'agit du modèle de pendule pesant le plus simple. Il est parfois appelé pendule de gravité idéal et, par opposition, tout pendule de gravité réel est appelé pendule pesant composé[1]. Par extension, on appelle aussi parfois pendule simple un dispositif dans lequel le fil inextensible est remplacé par une tige rigide de masse nulle pouvant tourner sans frottement dans un plan vertical autour de son extrémité fixe (liaison parfaite).
Il est possible d'approcher expérimentalement cet objet théorique en suspendant une masse de faible dimension au bout d'un fil (voir illustration). À cause de sa nature relativement simple, il se prête à des études théoriques poussées sur le plan mathématique. Ces études ont trouvé plusieurs applications en physique théorique, notamment dans les systèmes harmoniques simples.

Sous l'effet de son poids, lorsque le pendule est écarté de sa position d'équilibre (la verticale), le point matériel de masse m se déplace sur un arc de cercle : l'effet du poids tendant constamment à ramener le pendule vers sa position d'équilibre stable, celui-ci se met à osciller.
Les équations du mouvement
Mise en équation
Dans cette mise en équation, le freinage du pendule dû à l'air ambiant est négligé.
On repère la position du pendule simple par l'angle θ qu'il fait avec la verticale descendante, après avoir choisi une orientation positive. Cet angle s'appelle élongation angulaire. On note l'accélération due à la pesanteur (g ≈ 9,81 m/s2 pour une latitude de 45° au niveau de la mer).
Bilan des forces :
- Le poids
- La tension de la tige, toujours perpendiculaire au mouvement circulaire de la masse G.
Dans ce modèle les autres forces sont oubliées, notamment les forces de frottement (dans la réalité, le pendule s'arrête d'osciller sous l'action des frottements).
Énergie mécanique du pendule : Soit l la longueur du pendule, et soit sa vitesse angulaire. La vitesse de la masse est alors .
- La somme de l'énergie cinétique du pendule et de son énergie potentielle de pesanteur, cette dernière étant prise nulle au point le plus bas, vaut :
Cette énergie mécanique totale est constante au cours du mouvement. En effet, la tension de la tige est à tout instant perpendiculaire au mouvement circulaire de G, et ne produit aucun travail, et le travail du poids est pris en compte dans l'énergie potentielle. En dérivant cette expression par rapport au temps, on obtient :
On exclut la solution évidente, , qui correspond au cas où le pendule est à l'arrêt. On divise alors par , ce qui donne l'équation suivante du mouvement :
où l'on a posé
- Cette équation peut également être déduite du principe fondamental de la dynamique , en projetant les deux forces et sur le vecteur unitaire tangent à la trajectoire dans le sens des θ croissant, et sur le vecteur unitaire normal à la trajectoire et dirigé vers le point de suspension du pendule. On obtient alors :
- ce qui donne le système :

Puits de potentiel :
Si on trace en fonction de θ le graphe de l'énergie potentielle mgl(1 − cos θ), on obtient la figure suivante. On a tracé en gris le niveau de l'énergie potentielle maximale 2mgl.
- Si l'énergie mécanique E du pendule se situe à un niveau E1 inférieur à 2mgl, le pendule est confiné dans un puits de potentiel. Il existe une élongation maximale θ0 du pendule pour laquelle la vitesse s'annule, et le pendule oscille périodiquement. On a alors :
- qui se simplifie en :
- .
- Si l'énergie E du pendule se situe à un niveau E2 supérieur à 2mgl, alors le pendule franchit les barrières de potentiel, sa vitesse angulaire ne peut s'annuler et le pendule tourne autour du point O.
Résolution
La résolution exacte des équations du mouvement du pendule simple fait appel aux fonctions elliptiques de Jacobi. À un niveau élémentaire, on se contente d'une résolution approchée pour de petites oscillations. Dans ce cas, en effet, on peut confondre sin(θ) avec θ et on obtient alors l'équation :
- avec, rappelons-le,
dont une solution (choisie de façon que θ s'annule pour t = 0) est :
- , de période .
Pour de plus grandes amplitudes, on peut utiliser pour la période la formule approchée de Borda :
- ;
Pour une énergie mécanique supérieure à 2mgl, le pendule tournoie de façon périodique. À grande vitesse V, la période de rotation est équivalente à .
Tension de la tige
Une quantité physique dépend de la masse du pendule : la tension de la tige (pour sa mesure, on peut coller sur la barre une jauge de déformation étalonnée).
On a vu plus haut que : et l'on sait que, dans le cas du pendule oscillant :
- , d'où
T varie entre mg cos(θ0) et mg (3 - 2cos(θ0)). Par exemple, pour θ0 = 90°, T varie entre 0 et 3mg. Si on remplace la tige par un fil, il faut prévoir un fil résistant à 3 kgf (kilogramme-force) pour une masse de 1 kg, sinon le fil casse et la masse part ensuite en trajectoire parabolique. L'expérience est facile à montrer et assez spectaculaire mais il faut trouver le fil qui ne s'étire pas trop avant de casser. Une mise en évidence facile de l'augmentation de la tension T est d'utiliser un fil élastique. Mais il ne s'agit plus du tout du même problème et ce n'est plus du tout élémentaire (cf botafumeiro).
Boucler la boucle
T s'annule pour certaines conditions initiales de lancement différentes de celle proposée ci-dessus, voire devient négative, la tige supportant alors la masse. Il est classique de montrer que, lancée du point le plus bas avec une énergie 2mgl, la masse arrivera au bout d'un temps infini au sommet du cercle (et le cas est intégrable aisément). On se doute que si la tige est remplacée par un fil (liaison unilatérale), la trajectoire ne sera pas : montée au sommet, puis chute à la verticale ; il y aura décrochage quand T sera nulle, c’est-à-dire pour θ tel que , ce qui correspond à un angle d'amplitude 132° et une hauteur h = l + 2/3 l. L'expérience est facile à faire avec un pendule dont la masse est une pièce trouée, glissant d'abord sur un demi-cercle rigide, puis se retrouvant "dans l'air" attachée à son fil pour la deuxième partie du mouvement (ou évidemment avec la jauge de contrainte).
Alors que pour une tige, il suffit que l'énergie E dépasse 2mgl pour que le pendule se mette à tourner (looping the loop), dans le cas d'un fil il faut une énergie cinétique initiale supérieure à afin que le fil reste tendu.
Grandes amplitudes et non-linéarité
On introduit progressivement la non-linéarité :
- d'abord en considérant le deuxième terme du développement du sinus.
- puis en traitant le cas général, qui nécessite l'utilisation des fonctions elliptiques de Jacobi K, sn, cn, dn.
Formule de Borda
On considère donc l'équation différentielle approchée, dite de Duffing, obtenue en remplaçant sin(θ) par :
On montre alors que la période dépend de l'amplitude. La formule de Borda donne :
Le terme négligé qui suit est . Cette formule suffit jusqu'à π/2, à 3 % de précision (1 + 10/64 = 1,156 au lieu de 1,18). Il en existe plusieurs démonstrations :
- La méthode des perturbations de Lindstedt-Poincaré consiste à modifier la solution en lui ajoutant une petite perturbation θ1 tout en modifiant également la pulsation du mouvement en ω0 + ω1. On cherche la valeur à donner à ω1 de façon que l'équation différentielle, simplifiée en se limitant aux perturbations du premier ordre, donne une solution θ1 bornée. Cette valeur de ω1 est de sorte que la pulsation retenue est . T étant proportionnel à l'inverse de ω, la formule de Borda en découle.
- Si on suppose l'oscillation quasi sinusoïdale, la raideur moyenne étant plus faible, on s'attend physiquement à une diminution de la pulsation. En utilisant la formule d'Euler , et en cherchant , il vient , d'où et .
- On peut préférer la démonstration suivante dite du viriel : ~
d'où par la formule de Wallis : , soit .
- L'équation du mouvement du pendule est complètement intégrable grâce aux fonctions elliptiques, ce qui fait l'objet du paragraphe qui suit. Il suffit alors d'effectuer un développement à l'ordre souhaité de la solution exacte.
Cas pleinement non linéaire
On considère le cas pleinement non linéaire. Écrivons la conservation de l'énergie mécanique
sous la forme :
- , avec .
Posons . Il existe trois cas :
- k < 1, le pendule oscille : h varie entre 0 et . On a :
- .
Entre 0 et , on a . Un petit angle élémentaire est parcouru pendant un intervalle de temps élémentaire . La période totale des oscillations est donc , et l'on montre que :
- avec .
où K, sn et cn sont des fonctions elliptiques de Jacobi, K étant tabulée ci-dessous.
| en degré | en radian | |||
|---|---|---|---|---|
| 10 | 0,175 | 1,00 | 1,00 | 1,00 |
| 20 | 0,349 | 1,01 | 1,01 | 1,01 |
| 30 | 0,524 | 1,02 | 1,02 | 1,02 |
| 40 | 0,698 | 1,03 | 1,03 | 1,03 |
| 50 | 0,873 | 1,05 | 1,05 | 1,05 |
| 60 | 1,047 | 1,07 | 1,07 | 1,07 |
| 70 | 1,222 | 1,09 | 1,10 | 1,10 |
| 80 | 1,396 | 1,12 | 1,14 | 1,14 |
| 90 | 1,571 | 1,15 | 1,18 | 1,18 |
| 100 | 1,745 | 1,19 | 1,22 | 1,23 |
| 110 | 1,920 | 1,23 | 1,28 | 1,30 |
| 120 | 2,094 | 1,27 | 1,34 | 1,37 |
| 130 | 2,269 | 1,32 | 1,42 | 1,47 |
| 140 | 2,443 | 1,37 | 1,50 | 1,60 |
| 150 | 2,618 | 1,43 | 1,60 | 1,76 |
| 160 | 2,793 | 1,49 | 1,71 | 2.01 |
| 170 | 2,967 | 1,55 | 1,83 | 2,44 |
| 180 | 3,142 | 1,62 | 1,96 |
La fonction K admet également le développement :
où est un coefficient binomial. En remplaçant k par et en se limitant aux deux premiers termes, on retrouve la formule de Borda.
- k = 1, cas limite correspondant à . On a :
Temps infini pour monter à la verticale
où cosh et tanh sont respectivement le cosinus et la tangente hyperboliques.
- k > 1, le pendule tournoie : v2 varie entre 2g(H - 2l) et 2gH. La période pour effectuer un tour est . Si H est très grand, compte tenu du fait que K(0) vaut π/2, on pourra vérifier que la période tend vers .
Il est parfois judicieux de prendre pour période le temps mis pour faire deux tours. En effet, pour k légèrement inférieur à 1, le pendule effectue une trajectoire de longueur voisine de 4π. Avec cette convention, on a alors [2].
On a également : où sn et dn sont des fonctions elliptiques de Jacobi.
Plan de phase

On appelle orbite de phase la représentation paramétrée en temps du couple , ou de fonctions monotones de celles-ci. Dans le graphe ci-dessous, θ est en abscisse et en ordonnée. On discerne :
- la région dite d'oscillation (en noir), dite en œil d'Horus ou en œil en amande. Chaque orbite est parcourue dans le sens inverse au sens trigonométrique et tourne autour des points d'équilibre stables S, correspond aux valeurs 0, 2π, 4π, etc de θ0.
- les deux régions de révolution (en rouge), soit positive (en haut), soit négative (en bas), correspondant au cas où le pendule tourne autour du point O.
- la séparatrice, en bleu, correspondant au cas limite où θ0 vaut π.
- les points d'équilibre stable S déjà évoqués.
- Les points d'équilibre instable I correspondant aux valeurs π, 3π, etc de θ0. Il faut un temps infini pour parcourir une orbite qui va d'un point I à un autre.
Il paraît clair dorénavant que si l'on établit un mécanisme quelconque qui peut soustraire ou ajouter une petite énergie au pendule au voisinage de l'élongation π, on aura un phénomène difficile à prévoir même s'il est déterministe : exemple, placer un tout petit pendule accroché à la masse m : on a ainsi un pendule double ; les oscillations non linéaires de ce pendule, lesté d'un tel minuscule pendule, laissent pantois quand on les enregistre : Poincaré fut, avec Liapunov, un des premiers à considérer ce genre de problème ; puis Birkhoff ; puis l'école russe entraînée par la haute figure de Kolmogorov, et puis celle de Bogoliubov et de Krylov, puis Arnold,... jusqu'au moment où un article de 1971 de Ruelle et Takens vint suggérer que la situation était normale dès que l'espace des phases était à trois dimensions ou plus (on utilise parfois l'expression 1.5 degré de liberté).
Étude fine au voisinage de la séparatrice
On s'intéresse au spectre de la vitesse juste au-dessus et au-dessous du niveau énergétique de la séparatrice. Sur cette séparatrice, le spectre est qualifié de mode soliton.
Rappel : la séparatrice et le mode soliton
Dans le cas de la séparatrice, l'équation du premier ordre s'écrit :
- avec et
La solution "soliton" est caractérisée par les équations suivantes :
Oscillations longues
Si l'énergie du pendule est très légèrement inférieure à 2gH (1 - k2 << 1), la différence avec le mode soliton est infime. La valeur de la vitesse est imperceptiblement la même et le mouvement est donc quasi identique, sauf pour les moments où elle va s'annuler. La période est finie et vaut , valeur obtenue en utilisant la valeur approchée au voisinage de k = 1.
Tournoiements longs
De même, si l'énergie est très légèrement supérieure à 2gH (k2 - 1 << 1), le mouvement est quasi identique (mode soliton), sauf que la vitesse ne s'annule jamais et que l'élongation devient fonction monotone en quasi-escalier de marches de hauteur 2π en forme de sigmoïdes (kinks en anglais), longues d'une période très grande mais finie : . On remarque l'apparition d'un 2 au dénominateur, qui est un artefact dû au fait que dans un cas, on calcule la période sur un aller et retour (soit 4π environ), alors qu'un tournoiement s'effectue sur 2π. C'est une des raisons d'examiner le "pendule à gazette" soigneusement.
Anharmonicité

On trouve donc que v2 ou h sont bien les mêmes fonctions de période . Ci-dessous, l'allure de v2 au voisinage de k = 1. L'allure du graphe est la même, que k soit légèrement supérieur à 1 ou légèrement inférieur.
On caractérise le taux d'anharmonicité par l'étendue du spectre (discret puisque la fonction est périodique). A la limite :
- H = 2l, |v| est
Or, le spectre d'un peigne de Dirac est un peigne de Dirac (théorème de Poisson)
Le pendule simple est l'exemple le plus élémentaire qui montre :
- à faible amplitude : la linéarisation et donc le monochromatisme
- à amplitude critique : tous les harmoniques sont présents avec même amplitude.
Expérimentalement, on lance un pendule de Mach en tournoiement : les frottements faibles feront transiter d'un mode à l'autre. La projection de la boule sur l'axe portant h, elle, ne manifestera pas de transition : il y a continuité du phénomène.
Étude approfondie du spectre
Le développement en série de Fourier des fonctions de Jacobi sn, cn et dn sont connues. On en déduit un développement en série de Fourier de la vitesse angulaire.
Cas k > 1 : soit N = T/T0, avec T la période pour effectuer deux tours, correspondant à une rotation de 4π. N vaut . Nous prendrons comme pulsation fondamentale du mouvement . On a :
avec , et . Si k est très grand, le mouvement est un mouvement de rotation autour de O à très grande vitesse. q est très petit, et le mouvement s'effectue quasiment selon la loi . Quand k diminue, q augmente, de sorte que les a2n prennent de l'importance. Lorsque k est très légèrement supérieur à 1, N est très grand, et est très proche de 1. Le spectre est très étendu, puisque, pour n ~ N, an vaut encore environ 0,17.
Ci-dessous, les spectres de fréquence, par valeurs décroissantes de k, depuis une grande valeur jusqu'à une valeur légèrement supérieure à 1. En abscisse, on a porté les indices pairs 2n et en ordonnées les valeurs de a2n (on a pris a0 = 2) :
- k
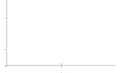 Grande valeur de k
Grande valeur de k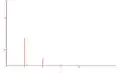 Valeur intermédiaire
Valeur intermédiaire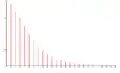 Valeur légèrement supérieure à 1
Valeur légèrement supérieure à 1
Cas k < 1 : la valeur de N est cette fois . La pulsation du mouvement est toujours . On a :
avec , et . La situation où k est très légèrement inférieur à 1 est comparable à celle où k est très légèrement supérieur à 1. Lorsque k diminue, q décroît, et lorsque k est proche de 0, la pulsation prépondérante est celle qui correspond à ω.
Ci-dessous, les spectres de fréquence, par valeurs décroissantes de k, depuis une valeur légèrement inférieure à 1 jusqu'à une valeur très petite. En abscisse, on a porté les indices impairs 2n + 1 et en ordonnées les valeurs de a2n+1 :
- k < 1 : spectre du pendule simple
 Valeur légèrement inférieure à 1
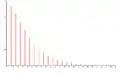
Valeur légèrement inférieure à 1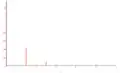 Valeur intermédiaire
Valeur intermédiaire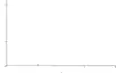 Très petite valeur de k
Très petite valeur de k
Voici également la représentation graphique de et la représentation des sommes partielles de Fourier correspondantes, d'une part pour k inférieur à 1, d'autre part pour k supérieur à 1 :
- Série de Fourier du pendule simple
 k < 1
k < 1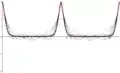 k > 1
k > 1
Pendule simple amorti
- Niveau élémentaire
En petites oscillations, le problème a déjà été étudié ; il est simple si le régime est de Stokes ou si l'amortissement est de type friction solide.
- Niveau élevé
Dans le cas où l'on prend en compte la résistance de l'air qui, aux vitesses en jeu, n'est pas en régime de Stokes (en -kv), mais en régime de fort nombre de Reynolds (en -kv2), comment tracer les séparatrices ? Comment trouver combien de tours fait le pendule avant d'osciller ?
- Nombre de tours
il se trouve que ce problème est analytiquement soluble :
Si , le pendule effectuera n tours avant d'osciller.
Cette indication suffit à tracer une esquisse de portrait de phase assez correcte.
- L'air
Le fait est que la pression de l'air joue un rôle, de l'ordre de quelques secondes par jour pour une pendule. Et il existe un minimum de la période en fonction de la pression.
Cela n'a plus vraiment d'importance aujourd'hui car les pendules sont systématiquement recalées sur l'émetteur GPS et plus tard peut-être sur l'émetteur du système Galileo.
Histoire des sciences
L'analyse de Torricelli
Dans le cas de petites oscillations, Evangelista Torricelli est certainement un des premiers à obtenir une mesure du coefficient 2π en partant de considérations sur la chute ralentie.
On peut, pour considérer le mouvement du pendule d'amplitude 3θ0, l'approximer par une chute sur un plan incliné de 2θ0, de longueur , suivie d'une trajectoire horizontale de C en A, de longueur BC/2.
On aura ainsi le quart de la trajectoire. La période T dans cette cuvette BCAC'B' est :
soit par approximation, soit une approximation de π :
- .
Une autre approximation donne .
Mais mieux encore, Torricelli remarque à juste titre que
- , avec
soit
- .
Il lui suffit de vérifier que la fonction sinus satisfait l'équation et il a le résultat. En bon élève de Cavalieri, est-il capable de faire ce raisonnement avant 1647 ? La mystérieuse cassette ayant disparu à sa mort, on ne saura sans doute jamais rien de ses travaux ultimes.
En tout cas, son disciple (via Mersenne), Huygens, trouve la valeur de 2π avant 1659, et montre que la courbe telle que exactement est la cycloïde. Rappelons que Dettonville publie son Traité de la Roulette en .
Remarque : ces termes sont anachroniques : g n'existe pas encore, car il n'y aura des unités que tard dans le siècle mais on compare au temps de chute libre de la hauteur H = l : ce fameux rapport : , qui intriguait Mersenne.
L'isochronisme
La section qui suit emprunte aux Études galiléennes d'Alexandre Koyré.
Il pourrait paraître surprenant que Galilée et ses élèves n'aient pas vu ce phénomène, alors que 4K devient infini lorsque les amplitudes pendulaires tendent vers 180°. Or, Galilée a affirmé que les oscillations du pendule étaient isochrones (voir pendule pesant). Il s'agit d'une cécité expérimentale, qui vaut la peine d'être mise en exergue.
- À la décharge de Galilée, il opérait vraisemblablement avec des fils (liaison unilatérale), donc le lancement sans vitesse initiale (chute « libre ralentie ») s'effectuait avec une amplitude inférieure à 90° : on pourra s'essayer[3] à retracer (sans regarder les valeurs tabulées) les valeurs de 4K. À 18 % près, 4K est constante dans ces conditions : Galilée a donc pu se laisser abuser.
- À la charge de Galilée, Koyré fait remarquer que c'est peu vraisemblable : si l'on dispose de plusieurs pendules identiques, on constate immédiatement le non-isochronisme : le déphasage est visible au bout de 10 oscillations. Or Galilée prétend avoir observé les oscillations sur de plus grands nombres. Mais il avait une thèse à défendre : l'isochronisme. Plus vraisemblablement, il a défendu des positions personnelles, philosophiques.
- Compte tenu de la résistance de l'air et du problème de la pseudo-période des oscillations amorties,
Compte tenu du fait que ce même problème de la résistance de l'air a dû être écarté avec la chute libre,
Compte tenu du fait qu'à 90°, un pendule à boule de liège et un pendule à boule d'acier ne se comportent pas de la même manière, il est vraisemblable que l'attitude de Galilée n'était pas malhonnête : les différences ont été portées sur le compte de la résistance de l'air. - Le texte cité de Galilée dans le Dialogo est donc à prendre avec précaution, ainsi que la conclusion qui en est tirée. Une preuve en est la lettre de Mersenne au jeune Huygens : après avoir dit grande merveille de Torricelli, la question est posée : qu'en est-il du facteur K(k)/K(0) (en notations modernes) ?
Notes et références
- 1 2 Élie Lévy, Dictionnaire de Physique, Presses universitaires de France, Paris, 1988, page 596.
- ↑ Voir Alain Chenciner, « Connaissez-vous le pendule ? », Gazette des mathématiciens, , p. 21-27 (lire en ligne).
- ↑ Grâce à la simulation présentée dans Geneviève Tulloue, « Période du pendule pesant », sur Université de Nantes.
Articles connexes
- Balançoire : analyse classique d'un cas l() résonant
- Botafumeiro : encensoir de Saint-Jacques de Compostelle : résonance paramétrique
- Oscillateur harmonique
- Oscillation pendulaire de marée : il s'agit de la libration des satellites
- Oscillateur harmonique et pendule simple en mécanique hamiltonienne : intégrateur symplectique
- Pendule (physique)
- Pendule adiabatique : une curiosité préquantique.
- Pendule balistique : en apparence élémentaire
- Pendule conique et pendule de Huygens : curiosité d'histoire.
- Pendule cycloïdal : ce pendule imaginé par Huygens a la propriété d'avoir une période d'oscillation qui ne dépend pas de l'amplitude du mouvement.
- Pendule de Bessel : ici, l(t) = l0 + v0t.
- Pendule de Kater : examine la métrologie de mesure pendulaire de g
- Pendule de Newton : système constitué de plusieurs pendules
- Pendule double
- Pendule elliptique : se ramène facilement au pendule simple
- Pendule entretenu par ancre : base de l'horlogerie
- Pendule inversé : à condition d'asservir, via le théorème de Kapitza
- Pendule simple de longueur variable : on y obtient l'équation générale de petites oscillations.
- Pendule simple discret : méthode résolution pas à pas du mouvement.
- Pendule simple à résonance paramétrique : a contrario étudie les équations type de Mathieu.
- Pendule sphérique : difficile, mais intégrable via les fonctions de Jacobi présentées ci-dessus.
- Pendule sphérique magnétique : rajoute au précédent la force d'un monopôle situé en O.




































![{\displaystyle \sin ^{3}x={3 \over 4}\sin x-\left[{1 \over 4}\sin(3x)\right]_{\mathrm {omis} }}](https://img.franco.wiki/i/22aea18d69e2253a178c8eecdbc80732966d2345.svg)











































































