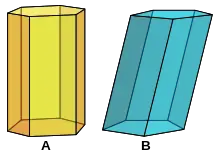
Un prisme est un solide géométrique délimité par deux polygones, appelés les bases du prisme, images l'un de l'autre par une translation. Ces bases sont reliées entre elles par des parallélogrammes.
Quand ces parallélogrammes sont des rectangles, on dit que le prisme est droit.
En géométrie affine, un prisme est un cas particulier de polyèdre. C'est un cylindre dont la base est polygonale.
Définitions

Une droite (d) de direction constante se déplaçant le long d'un polygone (p) décrit une surface appelée surface prismatique de polygone directeur (p) et de génératrice (d). Un prisme est le solide délimité par cette surface et par deux plans parallèles. Les sections définies par les deux plans parallèles sont appelées les bases du prisme. La distance séparant les deux bases est appelée hauteur du prisme.
Lorsque le plan est perpendiculaire à la droite génératrice (d), le prisme est appelé prisme droit. Lorsque le prisme est droit, les faces latérales sont des rectangles[1].
Propriétés
Le volume d'un prisme quelconque est égal au produit S × h, où S désigne l'aire d'une des deux bases (elles ont la même aire) et h la hauteur du prisme.
L'aire latérale d'un prisme droit est égale au produit p × h, où p désigne le périmètre d'une des deux bases et h la hauteur du prisme.
Si la base du prisme est un polygone à n côtés, le prisme a n + 2 faces, 3n arêtes et 2n sommets.
Exemples

Exemples de prismes droits :
- Le cube : toutes les faces sont des carrés.
- Le parallélépipède rectangle (le pavé) : toutes les faces sont des rectangles.
_(14597129638).jpg.webp)
- Le prisme droit à base triangulaire (par exemple, la boîte de chocolat de marque Toblerone).
- Les prismanes.
Autres exemples de prismes :
- Le parallélépipède quelconque : les faces sont des parallélogrammes.
- Le rhomboèdre : les faces sont des losanges égaux.
La généralisation d'un prisme aux autres dimensions est l'hyperprisme.
Notes et références
- ↑ « Lexique : Prisme droit », sur assistancescolaire.com (consulté le )
Articles connexes
- Polyèdre uniforme prismatique (en)
- Tronc (géométrie)
- Scutoïde
- Prismatoïde