Relation d'ordre

Une relation d'ordre est une relation binaire réflexive, antisymétrique et transitive : soit E un ensemble ; une relation interne ≤ sur E est une relation d'ordre si pour tous x, y et z éléments de E :

• x ≤ x (réflexivité)
• (x ≤ y et y ≤ x) ⇒ x = y (antisymétrie)
• (x ≤ y et y ≤ z) ⇒ x ≤ z (transitivité)

La forme même de ces axiomes permet d'affirmer que ces derniers sont également vérifiés par la relation binaire réciproque ≥, définie par

y ≥ x si et seulement si x ≤ y.

À toute relation d'ordre est donc associée une relation d'ordre opposée sur le même ensemble ; les formules x ≤ y et y ≥ x se lisent indifféremment : « x est inférieur à y », ou « x est plus petit que y », ou « y est supérieur à x », ou « y est plus grand que x » (ou parfois « x est au plus égal à y », ou « y est au moins égal à x»)^[1].

On associe également à toute relation d'ordre ≤, une relation dite d’ordre strict notée alors < (qui n'est pas une relation d'ordre au sens défini précédemment puisque la réflexivité n'est pas satisfaite), qui est la restriction de la relation d'ordre aux couples d'éléments distincts :

x < y si et seulement si x ≤ y et x ≠ y.

La formule x < y s'écrit aussi y > x, et se lit : « x est strictement inférieur à y », ou « x est strictement plus petit que y », « y est strictement supérieur à x », ou « y est strictement plus grand que x »^[2].

Pour éviter toute confusion, une relation d'ordre au sens de la définition générale (réflexive et antisymétrique) est parfois qualifiée d’ordre large.

Certaines relations d'ordre sont des relations totales, c'est-à-dire que deux éléments de E sont toujours comparables : pour tous x, y de E :

x ≤ y ou y ≤ x.

On dit alors que ≤ est une relation d'ordre total, et que l'ensemble E est totalement ordonné par cette relation. Une relation d'ordre sur E est dite partielle si elle n'est pas totale, et E est alors partiellement ordonné. Il est à noter qu'en anglais, on désigne par ordre partiel un ordre quelconque, qui peut donc être total. Cette terminologie est parfois également utilisée en français.

Ensemble ordonné

Un ensemble ordonné est un ensemble muni d'une relation d'ordre. Si un ensemble ordonné est fini, il peut être représenté graphiquement sous la forme d'un diagramme de Hasse, de façon similaire à la représentation habituelle d'un graphe sur papier, ce qui peut permettre de travailler plus aisément dessus. S'il est infini, on peut dessiner une partie de son diagramme de Hasse.

Exemples et contre-exemples

Fig. 1. Diagramme de Hasse de l'inclusion, sur l'ensemble des parties d'un ensemble à 3 éléments.

Fig. 2. Diagramme de Hasse de la relation de divisibilité pour les entiers entre 0 et 9.

• La relation « est inférieur (ou égal) à » est une relation d'ordre total sur l'ensemble des entiers (naturels ou relatifs), sur l'ensemble des rationnels ou l'ensemble des réels.
• Étant donné un ensemble ordonné (E, ≤), l'ordre lexicographique sur l'ensemble des n-uplets d'éléments de E est l'« ordre du dictionnaire », plus simple à définir par son ordre strict associé : (x₁, … , x_n) < (y₁, … , y_n) si x_i = y_i pour tous les indices i jusqu'à un certain k < n et x_k+1 < y_k+1.
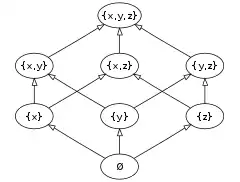
• La relation d'inclusion, « est un sous-ensemble de » ou « est contenu dans », est une relation d'ordre sur l'ensemble E des parties d'un ensemble X. Si X est fini, E est fini (plus précisément si X contient n éléments, E en contient 2ⁿ). La figure 1 représente le diagramme de Hasse de (E, ⊂) pour n = 3.
• Toute restriction à une partie F de E d'un ordre sur E est un ordre sur F. En particulier (d'après le point précédent) : sur n'importe quel ensemble F de parties d'un ensemble X, l'inclusion est une relation d'ordre — cet « exemple » est en fait générique : tout ordre est isomorphe à un ordre de cette forme^[3] ;
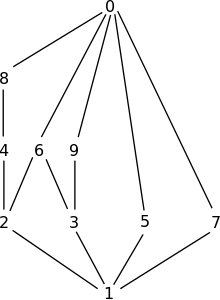
• La relation de divisibilité est une relation d'ordre partiel sur les entiers naturels. La figure 2 représente le diagramme de Hasse de sa restriction aux entiers de 0 à 9.
• L'ordre d'inclusion (cf. ci-dessus), sur l'ensemble des parties d'un produit cartésien U×V, est la finesse relative des relations binaires de U dans V. Pour V = U, cette relation permet par exemple (par restriction, cf. ci-dessus) de comparer entre elles :
  • les relations d'équivalence sur U (ou, ce qui revient au même : les partitions de U) ;
  • les relations d'ordre sur U.
• Étant donné une famille (E_i)_i∈I d'ensembles ordonnés, l'ordre naturel sur l'ensemble produit ∏_i∈IE_i est l'ordre produit, défini par :(x_i)_i∈I ≤ (y_i)_i∈I si et seulement si pour tout indice i, x_i ≤ y_i.Par exemple sur l'ensemble E^I des fonctions de I dans un ensemble ordonné E, l'ordre produit est donné par : f ≤ g si pour tout i ∈ I, f(i) ≤ g(i). Pour l'ordre produit sur ℝ^ℝ, une fonction est plus petite qu'une autre si sa courbe est toujours en dessous de l'autre courbe.
• On peut généraliser l'ordre lexicographique (mentionné en début de liste) de la façon suivante^[4] : si I est bien ordonné, on définit un ordre sur ∏_i∈IE_i par :(x_i)_i∈I < (y_i)_i∈I si et seulement s'il existe des indices i pour lesquels x_i ≠ y_i et si, pour le plus petit d'entre eux, on a x_i < y_i.Si les ordres sur les E_i sont totaux, l'ordre lexicographique sur ∏_i∈IE_i l'est aussi (mais pas en général l'ordre produit).
• Une relation de préordre n'est pas une relation d'ordre en général car il manque la propriété d'antisymétrie. Mais tout quotient d'un préordre par la relation d'équivalence associée est un ordre.
• Une relation d'ordre strict sur un ensemble non vide n'est pas une relation d'ordre car elle n'est pas réflexive. Mais si < est un ordre strict sur E, la relation « x < y ou x = y » est un ordre sur E.
• Une relation d'ordre cyclique n'est pas une relation d'ordre car c'est une relation ternaire. Mais les relations binaires obtenues en fixant l'un de ses trois arguments sont des relations d'ordre strict.
• Un arbre enraciné est un graphe orienté acyclique associé à une relation d'ordre partiel particulière, importante en informatique.

Applications monotones

Si (E, ≤) et (F, ≼) sont deux ensembles ordonnés, une application f de E dans F est dite croissante (ou parfois croissante au sens large, ou isotone^[5]) quand elle conserve l'ordre, décroissante (au sens large), ou antitone^[5] quand elle inverse celui-ci, c'est-à-dire que :

f est croissante quand pour tous x et y de E, x ≤ y ⇒ f(x) ≼ f(y) ;

f est décroissante quand pour tous x et y de E, x ≤ y ⇒ f(x) ≽ f(y).

Elle est dite strictement croissante quand elle conserve l'ordre strict : pour tous x et y de E, x < y ⇒ f(x) ≺ f(y),

et strictement décroissante quand elle l'inverse : pour tous x et y de E, x < y ⇒ f(x) ≻ f(y).

À noter que si une application croissante de (E, ≤) dans (F, ≼) est injective alors elle est strictement croissante, mais que la réciproque est fausse en général (elle est vraie cependant si l'ordre sur E est total)^[6].

Une application monotone ou monotone au sens large (resp. strictement monotone) est une application croissante ou décroissante (resp. strictement croissante ou strictement décroissante).

La bijection réciproque d'une bijection croissante f : (E, ≤) → (F, ≼) n'est pas nécessairement croissante (prendre par exemple^[7] l'application identité, de E = ℝ muni de l'ordre d'égalité dans F = ℝ muni de l'ordre usuel). Elle l'est cependant si ≤ est total (si f⁻¹(y₁) ≥ f⁻¹(y₂) alors, par croissance de f, y₁ ≽ y₂. Donc par contraposée : si y₁ ≺ y₂ et si ≤ est total alors f⁻¹(y₁) < f⁻¹(y₂)).

Un isomorphisme entre deux ensembles ordonnés (E, ≤) et (F, ≼) est une bijection f de E dans F qui est croissante et dont la réciproque est croissante, ce qui revient à dire que f est bijective et vérifie pour tous x et y de E :

x ≤ y ⇔ f(x) ≼ f(y)^[8].

Un plongement d'ensembles ordonnés de (E, ≤) dans (F, ≼) est une application f de E dans F vérifiant pour tous x et y de E :

x ≤ y ⇔ f(x) ≼ f(y)

(une telle application est forcément injective). Les isomorphismes d'ordres sont donc les plongements surjectifs^[8].

Dans la catégorie des ensembles ordonnés, les morphismes sont par définition les applications croissantes^[9], et les isomorphismes sont, par conséquent, ceux introduits ci-dessus.

Plus grand élément et élément maximal

Dans un ensemble ordonné E, il n'existe pas forcément de plus grand élément. Si E est fini, il contiendra (au moins) un élément maximal. Si E est un ensemble inductif infini, le lemme de Zorn garantit encore l'existence d'un élément maximal.

Relation d'ordre strict

On a vu qu'à une relation d'ordre ≤ sur un ensemble E, on associait naturellement une relation < sur E, qui est alors une relation d'ordre strict, c'est-à-dire antiréflexive (x < x n'est vrai pour aucun élément x de E) et transitive.

Or toute relation d'ordre strict est antisymétrique et même asymétrique (ce qui équivaut à : antisymétrique et antiréflexive), c'est-à-dire que pour tous x et y :

x < y ⇒ non (y < x).

Par conséquent, réciproquement, à toute relation d'ordre strict < sur E, on peut associer une relation d'ordre ≤ sur E en posant :

x ≤ y si et seulement si x < y ou x = y.

On vérifie facilement qu'en mettant bout à bout ces deux constructions, à partir d'un ordre ou d'un ordre strict, on retrouve la relation de départ. Choisir l'une ou l'autre des axiomatisations n'a donc pas d'importance en soi.

Pour un ordre strict, la totalité s'exprime ainsi :

∀ x, y ∈ E ( x < y ou x = y ou y < x ).

et l'on dit alors que c'est une relation d'ordre strict total^[10]. Il n'y a pas de confusion possible avec la notion de relation totale, car les relations d'ordre strict sont antiréflexives, tandis que les relations totales sont réflexives.

Pour un ordre strict total, les trois possibilités — x < y, x = y et y < x — sont exclusives, et l'on parle parfois, à la suite de Cantor, de propriété de trichotomie.

Relation acyclique

La clôture réflexive transitive d'une relation R est une relation d'ordre — ou encore : la clôture transitive de R est antisymétrique — si et seulement si R est acyclique.

La clôture transitive de R est un ordre strict si et seulement si R est strictement acyclique, c'est-à-dire si son graphe est acyclique.

Négation (ou complémentaire) d'une relation d'ordre

La négation d'une relation binaire ${\displaystyle R}$ définie sur un ensemble ${\displaystyle A}$ est la relation de graphe le complémentaire de celui de ${\displaystyle R}$ dans ${\displaystyle A\times A}$. On la note ${\displaystyle \not \!R}$. Dit autrement, deux éléments sont en relation par ${\displaystyle \not \!R}$ si et seulement s'ils ne le sont pas par ${\displaystyle R}$.

Dire qu'un ordre est total, c'est dire que sa négation est l'ordre strict inverse. C’est-à-dire qu'il y a équivalence pour un ordre ${\displaystyle \leqslant }$ entre :

• ${\displaystyle \leqslant }$ est total ;
• ${\displaystyle x\not \leqslant y\iff y<x}$.

Par contre, dès qu'il existe deux éléments distincts non comparables par un ordre, sa négation ne peut être un ordre (strict ou large), car elle n'est pas antisymétrique. La négation d'un ordre non total n'est donc jamais un ordre.

Par exemple, la négation de l'inclusion ⊄ sur l'ensemble des parties d'un ensemble d'au moins deux éléments n'est pas un ordre, car, si a ≠ b, on a toujours {a}≠{b} avec cependant {a}⊄{b} et {b}⊄{a}.

Ordre dual

L'ordre dual (ou ordre opposé^[11]) d'un ensemble ordonné P = (E, ≤) est l'ensemble ordonné P^op = (E, ≤^op), où ≤^op est la relation d'ordre opposée de ≤, c'est-à-dire la relation ≥ (on utilise parfois * au lieu de ^op)^[11],[12].

Le bidual (P^op)^op de P est égal à P.

Préordre

Un préordre est une relation binaire réflexive et transitive.

Tout préordre ℛ sur un ensemble E induit une relation d'ordre sur l'ensemble E quotienté par la relation d'équivalence ~ définie par « x~y si et seulement si (xℛy et yℛx) ».

Pour plus de précisions et des exemples, voir l'article détaillé.

Compatibilité

La compatibilité d'une relation d'ordre avec une structure algébrique ne se définit qu'au cas par cas^[13].

• Un ordre ≤ sur un demi-groupe (G, +) est dit compatible si, pour tous x, y et z dans G tels que x ≤ y, on a x + z ≤ y + z et z + x ≤ z + y.
  Lorsque (G, +) est un groupe, on dit alors que (G, +, ≤) est un groupe ordonné, et qu'un élément est positif s'il est supérieur à l'élément neutre.
  Tout groupe totalement ordonné archimédien est abélien et se plonge dans (ℝ, +, ≤).
• Un anneau ou un corps (A, +, ×) est dit ordonné s'il est muni d'un ordre ≤ tel que (A, +, ≤) soit un groupe ordonné et que le produit de deux éléments positifs soit positif.
  Tout corps totalement ordonné archimédien se plonge dans (ℝ, +, ×, ≤).
  Dans un corps totalement ordonné, –1 n'est jamais un carré ni même une somme de carrés.
• Un espace vectoriel ordonné est un espace vectoriel réel (E, +, ∙) muni d'un ordre ≤ tel que (E, +, ≤) soit un groupe ordonné et que tout vecteur produit d'un réel positif par un vecteur positif soit positif.

Ensemble bien ordonné

Un ensemble ordonné est dit bien ordonné si tout sous-ensemble non vide de cet ensemble possède un plus petit élément.

Treillis

Un ensemble est appelé treillis s'il est ordonné et si tout couple d'éléments possède une borne supérieure et une borne inférieure.

Topologie de l'ordre

Un ensemble ordonné peut être muni de plusieurs topologies issues de l'ordre : la topologie de l'ordre, la topologie de l'ordre à droite et la topologie de l'ordre à gauche.

Liens avec les complexes simpliciaux

Une classe importante de complexes simpliciaux provient d'ensembles ordonnés finis. On définit le complexe d'ordre D(P) d'un ensemble ordonné fini P comme étant l'ensemble des chaînes de P. Le complexe d'ordre est trivialement un complexe simplicial.

L'étude de l'ensemble ordonné en lui-même donne des informations sur son complexe d'ordre, et il est donc intéressant d'étudier un complexe simplicial comme le complexe d'ordre d'un ensemble ordonné.

Articles connexes

Bibliographie

• (en) Richard P. Stanley, Enumerative Combinatorics, vol. 1 [détail des éditions] (présentation en ligne)
• (en) Efe A. Ok, Order Theory and its Applications (lire en ligne)