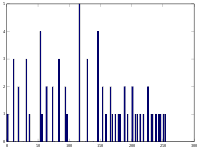
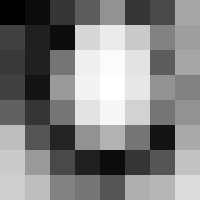تسوية المدرج التكراري ( Histogram equalization) هي تقنية مستخدمة في معالجة الصور الرقمية، حيث يتم تعديل تباين الصورة وجعل المدرج التكراري الخاص بها منبسط وموزّع قدر الإمكان.
نظرة عامة
هذه الطريقة عادة تعمل على زيادة التباين الكلي للعديد من الصور، خاصة عندما يتم تمثيل البيانات القابلة للإستخدام بقيم تباين قريبة من بعضها البعض. خلال عملية الضبط، تتوزع قيم شدة الإضاءة بشكل أفضل على المدرج التكراري للصورة. هذا يسمح للمناطق ذات التباين الموضعي القليل أن تكسب تباينًا أكبر. تنجز عملية تسوية المدرج التكراري ما سبق، من خلال بسط قيم شدة الإضاءة الأكثر تكرارًا بكفاءة.
هذه الطريقة مفيدة في الصور التي تكون فيها كلا اللوحتين الأمامية والخلفية فيها ساطعتان أو غامقتان. بشكل خاص، بالإضافة إلى ذلك هذه التقنية تؤدي للحصول على مظهر أفصل لتركيب العظام في صور الأشعة السينية، وتفاصيل أكثر وضوحًا في الصور الفوتوغرافية التي تعرضت للضوء بشكل زائد عن الحد أو أقل مما ينبغي. الفائدة الرئيسية من هذه الطريقة هي أنها أسلوب تقني مستقيم وأيضًا عملية قابلة للعكس. اذًا نظريًا، إذا عُرفت وظيفة تسوية المدرج التكراري يمكن استعادة المدرج التكراري الأصلي للصورة. وجدير بالذكر أنها لا تحتاج لعدة حسابات. بينما من مساوئ هذه الطريقة أنها عشوائية وغير مميزة. فممكن أن تزيد التباين لضجيج الخلفية بينما تقلله للإشارة المهمة القابلة للاستخدام. في التصوير العلمي الذي يتميز بالاهتمام بالترابط المكاني أكثر منه بشدة الإضاءة للإشارة (مثل انفصال أجزاء الحمض النووي الريبوزي منقوص الاوكسجين )بالإنجليزية : DNA) لأطوال مكماة )، نسبة الإشارة إلى الضوضاء القليلة تعيق عملية الكشف المرئي.
تسوية المدرج التكراري عادةً تنتج تأثير غير واقعي على الصور الفوتغرافية، بيد أنها مفيدة جدًا للصور العلمية مثل الصور الحرارية، صور الأقمار الصناعية و صور الأشعة السينية. بالإضافة إلى أن هذه العملية يمكن أن تنتج تأثيرات غير مرغوب بها (مثل التدرج المرئي للصور) عندما يتم تطبيقه على صور ذات عمق لوني قليل. على سبيل المثال، إذا تم تطبيقه على صورة مؤلفة من 8-بت تم عرضها بواسطة ثماني مستويات توزيع رمادية سيتم تقليل عمق الألوان (عدد المستويات الوحيدة المظللة بالرمادي) للصورة. تظهر عملية تسوية المدرج التكراري أكبر فاعلية لها حين يتم تطبيقها على الصور ذات العمق اللوني الكبير، مثل البيانات المستمرة أو الصور التي تحوي 16-بت من المستويات الرمادية.
هناك طريقتان للتفكير بتطبيق عملية تسوية المدرج التكراري للصورة، إما عبر تغيير الصورة أو تغيير مدى الألوان المستخدمة. يمكن التعبير عن الطريقة كعلاقة
P(M(I))
حيث أن I هي الصورة الأصلية، و M هي عملية تعيين تسوية المدرج التكراري، و P هو المدى. إذا قمنا بتعريف مدى جديد P` وحافظنا على الصورة I بدون تغيير إذًا تسوية المدرج التكراري تم تطبيقه على مستوى تغيير المدى للألوان. من ناحية أخرى، إذا بقي المدى P بدون تغيير وتم تعديل الصورة ل I` إذًا تسوية المدرج التكراري تم تطبيقه على مستوى تغيير الصورة. في أغلب الحالات تعتبر الطريقة الأولى أفضل لأنها تحافظ على الصورة الأصلية من التغيرات.
التعديلات على هذه الطريقة بإستخدام مدرجات تكرارية متعددة تسمى مدرجات تكرارية جزئية (بالإنجليزية : subhistograms)
جزئية لتحسين التباين الموضعي بدلًا من التباين الكلي. أمثلة على هذه الطرق تتضمن تسوية المدرج التكراري القابل للتكييف، تسوية المدرج التكراري القابل للتكييف المحدد للتباين (بالإنجليزية : CLAHE) تسوية المدرج التكراري ذو القمم المتعددة (بالإنجليزية : MPHE)
و تسوية المدرج الثنائي التكراري ذو الخصائص المثلى الأولية متعدد الإستخدامات (بالإنجليزية : MBOBHE)
الهدف من كل هذه الطرق، وبشكل خاص الطريقة الأخيرة، هو تحسين وتطوير التباين للصورة بدون عمل إزاحة على السطوع الخاص بها وبدون خسارة للتفاصيل عبر تعديل الخوارزمية الخاصة بتسوية المدرج التكراري.
تحويل الإشارة يكافئ عملية تسوية المدرج التكراري أيضًا تشبه ما يحدث في الشبكات العصبية البيولوجية إذ لزيادة معدل اضطرام المخرجات لعصبون ما تتم زيادة إحصائيات المدخلات. هذا تم إثباته بشكل جزئي في شبكية العين.
تسوية المدرج التكراري هي حالة خاصة من مستويات أكثر شمولية تسمى طرق إعادة تشكيل المدرج التكراري للصور. هذه الطرق تبحث عن تعديل الصورة لتسهيل تحليلها، ولتطوير جودة الرؤية (مثلًا مفهوم ثبات الألوان).
الإسقاط الخلفي
الإسقاط للمدرج التكراري للصورة هو إعادة تطبيق المدرج التكراري المعدل على الصورة الأصلية، ويؤدي عمله كما هو في الجداول الموضحة الخاصة بقيم النقاط الضوئية.
لكل مجموعة نقاط ضوئية تم أخذها من نفس الموقع من جميع الصور المدخلة أحادية القناة، الوظيفة هي أن يتم وضع قيم لخانات المدرج التكراري للصورة المقصودة، حيث أن المحاور للخانات يتم تحديدها عبر قيم النقاط الضوئية في المجموعة المدخلة. أما من الناحية الإحصائية، قيمة كل نقطة ضوئية في الصورة الناتجة تصف احتمالية أن مجموعة النقاط الضوئية المقابلة لها في الصورة المدخلة تنتمي للهدف الذي تم إنشاء المدرج التكراري لأجله.
التطبيق
عند إجراء تسوية للمدرج التكراري للصورة (x) ذات المستوى الرمادي (i) بحيث ان عدد النقاط (pixels) لها عند مستوى رمادي معين هو (ni)، فإن احتمالية ظهور النقطة عند مستوى رمادي معين في الصورة:
- حيث أن:
- L: العدد الكلي للمستويات الرمادية في الصورة
- n: العدد الكلي للنقاط في الصورة
p_x(i) : المدرج التكراري للصورة عند قيمة لونية معينة، حيث يتم قسمة القيم الناتجة على العدد الكلي للنقاط في الصورة (normalize [0,1])
كما يتم حساب التوزيع التراكمي (بالإنجليزية : Cumulative distribution function) للاحتمال (ps) :
حيث تكون قيم التوزيع التراكمي من 0 إلى 1 (normalized)
للحصول على صورة جديدة (y) ذات مستوى تكراري منبسط قدر الإمكان (بالإنجليزية : flat) فإننا بحاجة إلى التحويل y=T(x) . سيكون لهذه الصورة داله توزيع تراكمية خطيه (CDF) عبر نطاق القيمة، أي أن:
عند قيمة K معينة. خصائص التوزيع التراكمي تسمح لنا بإجراء مثل هذا التحويل، ويتم تعريف دالة التوزيع المعكوس ب:
حيث أن k ضمن الفترة [0,L]
يجب الإشارة إلى أنه عندما يكون التوزيع التكراري للصورة x ضمن النطاق [0,1]، فإن T تعمل على مطابقة القيم ضمن ذات النطاق، لإعادة القيم إلى نطاقها الأصلي نستخدم:
أمثلة
يجب أن يُستبدل التوزيع التراكمي (بالإنجليزية : Cumulative distribution function) بالرسم البياني التراكمي (بالإنجليزية :Cumulative histogram ) , خاصه وان المقالة ترتبط بداله التوزيع التراكمية المشتقة بقسمه القيم في الرسم البياني التراكمي على العدد الكلي للنقاط في الصورة.
صورة رمادية 8-بت تحتوي على القيم التالية:
| 52 | 55 | 61 | 59 | 79 | 61 | 76 | 61 |
|---|---|---|---|---|---|---|---|
| 62 | 59 | 55 | 104 | 94 | 85 | 59 | 71 |
| 63 | 65 | 66 | 113 | 144 | 104 | 63 | 72 |
| 64 | 70 | 70 | 126 | 154 | 109 | 71 | 69 |
| 67 | 73 | 68 | 106 | 122 | 88 | 68 | 68 |
| 68 | 79 | 60 | 70 | 77 | 66 | 58 | 75 |
| 69 | 85 | 64 | 58 | 55 | 61 | 65 | 83 |
| 70 | 87 | 69 | 68 | 65 | 73 | 78 | 90 |
التوزيع التكراري للصورة يظهر في الجدول التالي. يتم استبعاد قيم النقاط (بالإنجليزية:pixels) التي تحتوي علي عدد صفري من أجل الإيجاز.
Value Count Value Count Value Count Value Count Value Count 52 1 64 2 72 1 85 2 113 1 55 3 65 3 73 2 87 1 122 1 58 2 66 2 75 1 88 1 126 1 59 3 67 1 76 1 90 1 144 1 60 1 68 5 77 1 94 1 154 1 61 4 69 3 78 1 104 2 62 1 70 4 79 2 106 1 63 2 71 2 83 1 109 1
دالة التوزيع التكراري تظهر في الأسفل. مره أخرى، يتم استبعاد قيم النقاط (بالإنجليزية:pixels) التي لا تساهم في زيادة داله التوزيع التراكمي للإيجاز.
v, Pixel Intensity cdf(v) h(v), Equalized v 52 1 0 55 4 12 58 6 20 59 9 32 60 10 36 61 14 53 62 15 57 63 17 65 64 19 73 65 22 85 66 24 93 67 25 97 68 30 117 69 33 130 70 37 146 71 39 154 72 40 158 73 42 166 75 43 170 76 44 174 77 45 178 78 46 182 79 48 190 83 49 194 85 51 202 87 52 206 88 53 210 90 54 215 94 55 219 104 57 227 106 58 231 109 59 235 113 60 239 122 61 243 126 62 247 144 63 251 154 64 255
يظهر التوزيع التكراري أن الحد الأدنى للصورة الفرعية هو 52 وأن القيمة القصوى هي 154 . دالة التوزيع التراكمي 64 للقيمة 154 تتطابق مع عدد النقاط (بالإنجليزية:pixels) في الصورة. كما أنه يجب تحويل نطاق الصورة إلى .
الصيغة العامة لتسوية المدرج التكراري:
حيث أن:
cdfmin : القيمة الصغرى غير الصفرية في التوزيع التراكمي (في هذه الحالة 1)
M × N : عدد النقاط (بالإنجليزية:pixels) في الصورة ( في هذا المثال تساوي 64 , حيث M هو العرض و N هي الارتفاع )
L : عدد المستويات الرمادية المستخدمة
لاحظ أن قياسات القيم في القيم الأصلية أكبر من 0 , ضمن النطاق [1,L-1]، لذلك نستبدل المعادلة أعلاه ب:
حيث أن cdf(v) > 0، القياس من 1 إلى 255 يحافظ على عدم وجود أصفار من القيم الدنيا.
صيغة المعادلة للقياسات من 1 إلى 255:
على سبيل المثال، التوزيع التراكمي ل 78 هو 46. (يتم استخدام قيمه 78 في الصف السفلي من العمود السابع.) تصبح القيمة التي تم تطبيعها:
وبمجرد الانتهاء من ذلك ثم يتم أخذ قيم الصورة المتساوية مباشره من داله التوزيع التراكمي ضمن النطاق [1,255] لتحقيق القيم المتساوية:
| 0 | 12 | 53 | 32 | 190 | 53 | 174 | 53 |
|---|---|---|---|---|---|---|---|
| 57 | 32 | 12 | 227 | 219 | 202 | 32 | 154 |
| 65 | 85 | 93 | 239 | 251 | 227 | 65 | 158 |
| 73 | 146 | 146 | 247 | 255 | 235 | 154 | 130 |
| 97 | 166 | 117 | 231 | 243 | 210 | 117 | 117 |
| 117 | 190 | 36 | 146 | 178 | 93 | 20 | 170 |
| 130 | 202 | 73 | 20 | 12 | 53 | 85 | 194 |
| 146 | 206 | 130 | 117 | 85 | 166 | 182 | 215 |
لاحظ ان الحد الأدنى للقيمة (52) هو الآن 0 والقيمة القصوى (154) الآن 255.[1][2][3]
مراجع
- "إنشاء واستخدام المدرج التكراري—إنشاء الرؤى | الوثائق". doc.arcgis.com. مؤرشف من الأصل في 4 يناير 202004 يناير 2020.
- "المدرج التكراري Histogram". الإدارة والهندسة الصناعية. 2010-01-25. مؤرشف من الأصل في 12 يوليو 201704 يناير 2020.
- The Image Processing Handbook, Fourth Edition. CRC Press. 2002-07-26. . مؤرشف من الأصل في 17 مايو 2020.






![{\displaystyle [0,255]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b92f49fdc420e36b9d62c711c3c6ebe7d9fcebc)