معامل عزم القصور الذاتي أو عزم القصور الذاتي القطبي المعياري هو كمية فيزيائية لابُعدية، تستخدم في سياق علم دراسة الكواكب بغرض وصف توزيع الكتلة داخل الكواكب والأقمار الطبيعية في اتجاه أنصاف أقطارها. وبالنظر إلى أن عزم القصور الذاتي هو كمية فيزيائية تتناسب طرديًا مع الكتلة، ومع مربع المسافة، فلا بد من أن معامل عزم القصور الذاتي هو المعامل الذي يربط بين هذه الكمية وبين حاصل ضرب هاتين الكميتين. فعلى سبيل المثال، تخيل قضيبًا منتظم الكتلة مهمل الثخانة يدور حول طرفه المثبت، ومن ثم فإن عزم قصوره الذاتي (I) يساوي (1/3)ML2 ، وبالتالي فإن معامل عزم القصور الذاتي في هذه الحالة يساوي (1/3).
التعريف
بادئًا، دعنا نفترض أن عزوم القصور الذاتي الرئيسية الخاصة بأحد الأجرام السماوية هي (A, B, C) على حسب اتجاه محور الدوران، بحيث تكون (C>B>A). ومن هذا المنطلق يعرف معامل عزم القصور الذاتي بالقيمة الآتية:
- ,
حيث أن C هو عزم القصور الذاتي القطبي، و R هو نصف القطر المتوسط (أي نصف القطر الذي يسمح لنا بالتعامل رياضيًا مع الكوكب كما لو كانت كتلته بأكملها متركزة على بعد R من محور الدوران).[1][2] وقيمة هذا المعامل في حالة جسم كروي منتظم الكتلة تساوي 0.4 (وذلك حيث أن عزم القصور الذاتي الخاص بالأجسام الكروية يساوي (2/5)MR2). أما في حالة الكواكب والأقمار ذات الكتل غير المنتظمة، والتي تزداد كثافتها كلما اقتربنا من مركزها، فإن قيمة هذا المعامل أقل من (0.4).
وتُعد هذه الكمية مؤشرًا جيدًا على وجود أنوية مركزية بداخل الأجرام السماوية. حيث أن الأجسام التي تتركز معظم كتلتها داخل نواة مركزية تحيد عن سلوك الأجسام منتظمة الكتلة، والتي تتميز بمعامل 0.4. وكلما انحرفت قيمة ذلك المعامل عن 0.4، كلما زاد تركيز الكتلة بداخل نواة الجسم.
القيم الخاصة بالمجموعة الشمسية
وتحظى الشمس بأصغر معامل من بين جميع الأجرام السماوية التي تقع في حيز المجموعة الشمسية؛ فهي تحظى كذلك بأعلى كثافة مركزية (كثافة نواة الشمس تساوي 162 (162 g/cm3 وبالمقارنة فإن كثافة نواة الأرض تقدر بحوالي 13 g/cm^3 تقريبًا [3][note 1] compared to ~13 for الأرض[4][5]، وجدير بالذكر أن أنوية النجوم تزداد في كثافتها على مدار عمر النجم)، وهي تتميز أيضًا بكثافة متوسطة منخفضة نسبيًا (كثافة الشمس المتوسطة 1.41 g/cm^3 وبالمقارنة فإن كثافة الأرض المتوسطة 5.5 g/cm^3). أما كوكب زحل فهو يتميز عن بقية الكواكب الغازية بأقل معامل، وذلك يوعز إلى أنه يحظى بأقل كثافة ظاهرية من بين أشقائه (0.687 g/cm^3).[6] ويتميز قمر غانيميد بأقل معامل من بين جميع الأجسام الصلبة التي تقع داخل المجموعة الشمسية، وذلك بفضل كثافته المتدرجة كليًا،[7][8] والتي ترجع في سببها من جهة إلى ظاهرة الاحترار الجزري (Tidal heating) التي تحدث نتيجة الرنين المداري بينه وبين قمر أوروبا [9]، ومن جهة أخرى بسبب احتواء هذا القمر على كمية مهولة من الجليد المائي منخفض الكثافة. أما قمر كاليستو، فبالرغم من أنه متقارب في الحجم والتركيب، إلا أنه لا يتعرض إلى ذات التأثير الذي يتعرض إليه قمر غانيميد، مما يعني أن كتلته تتوزع بشكل منتظم أكثر بالمقارنة بغانيميد. والاعتقاد الشائع حاليًا عن قمر الأرض أنه يمتلك نواة مركزية ضئيلة الحجم، ولكن بغض النظر عن وجودها فإن كتلته الداخلية متجانسة إلى حد كبير.[10][11]
| الجسم | قيمة المعامل | مصدر القياس | ملاحظات |
|---|---|---|---|
| الشمس | 0.070 | [3] | غير مُقاس |
| عطارد | 0.346 ± 0.014 | [12] | |
| الزهرة | unknown[note 2] | ||
| الأرض | 0.3307 | [14] | |
| القمر | 0.3929 ± 0.0009 | [15] | |
| المريخ | 0.3662 ± 0.0017 | [16] | |
| سيريس | 0.36 ± 0.15[note 3] | [18] | غير مُقاس. القيمة المذكورة هي مجرد تقديرات مبنية على أساس فرضيات مختلفة عن معدل دوران الكوكب حول نفسه في بداية تكوينه.[18]) |
| المشتري | 0.2756 ± 0.0006 | [19] | |
| أيو | 0.37824 ± 0.00022 | [20] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| يوروبا | 0.346 ± 0.005 | [20] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| غانيميد | 0.3115 ± 0.0028 | [20] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| كاليستو | 0.3549 ± 0.0042 | [20] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| زحل | 0.22 | [21] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| إنسيلادوس | 0.3305 ± 0.0025 | [22] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| ريا | 0.3911 ± 0.0045 | [23] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| تيتان | 0.341 | [24] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| أورانوس | 0.23 | [25] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
| نبتون | 0.23 | [25] | غير مُقاس. تم حسابه عن طريق معادلة داروين-راداو |
طريقة القياس
والطريقة التقليدية المستخدمة في تحديد قيمة عزم القصور الذاتي القطبي هي الاستعانة بقياسات الكميات المغزلية (سرعة المبادرة المغزلية والميل المحوري) جنبًا إلى جنب مع الكميات الجذبوية (معاملات التوافقيات الكروية، والتي تستخدم في تمثيل المجال الجذبوي). ووفي العادة يستلزم لتحصيل تلك الكميات الجيوديسة مكوكًا فضائيًا يحوم في مدار يحيط بالكوكب الخاضع للدراسة.
طرق حساب تقريبية
تُستخدم معادلة داروين-راداو في تقدير معامل عزم القصور الذاتي الخاص بالأجسام في حالة الإتزان الهيدروستاتيكي، وذلك على أساس الخواص الشكلية، والمغزلية، والجذبوية.[26]
دوره في معرفة التركيب الداخلي
يلعب معامل عزم القصور الذاتي دورًا هامًا في التحقق من صحة النظريات التي تعني بوصف البنية الداخلية للكواكب والأقمار. فيجب على أي نموذج يصف شكل توزيع كتلة الأجرام السماوية أن يتماشى مع قيمة الكثافة الحجمية المقاسة، وأن يتوافق كذلك مع قيمة معامل عزم القصور الذاتي الخاص بهذا الجرم.
معرض صور تصف نماذج البنية الداخلية
الشمس (C/MR2 = 0.070)
زحل (C/MR2 = 0.22)
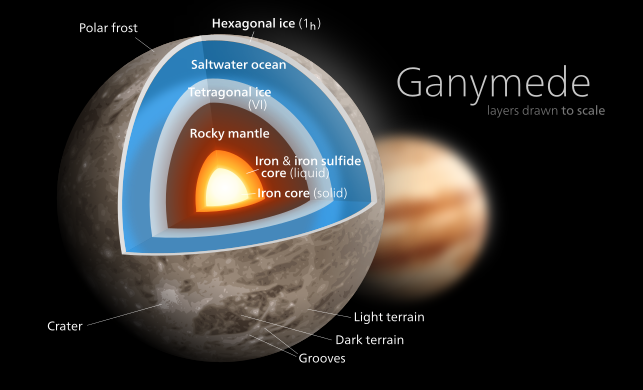
غانيميد (C/MR2 = 0.3115)
الأرض (C/MR2 = 0.3307)
كاليستو (C/MR2 = 0.3549)
القمر (C/MR2 = 0.3929)
المراجع
- Hubbard, William B. (1984). Planetary interiors. New York, N.Y.: Van Nostrand Reinhold. . OCLC 10147326. مؤرشف من الأصل في 15 فبراير 2017.
- de Pater, Imke; Lissauer, Jack J. (2015). Planetary sciences (الطبعة 2nd updated). New York: مطبعة جامعة كامبريدج. . OCLC 903194732. مؤرشف من الأصل في 2 مايو 2020.
- Williams, D. R. "Sun Fact Sheet". Planetary Fact Sheets. ناسا. مؤرشف من الأصل في 30 أكتوبر 201926 يناير 2017.
- Robertson, Eugene C. (26 July 2001). "The Interior of the Earth". الماسح الجيولوجي الأمريكي. مؤرشف من الأصل في 3 مايو 201924 مارس 2007.
- Hazlett, James S.; Monroe, Reed; Wicander, Richard (2006). Physical geology : exploring the earth (الطبعة 6.). Belmont: Thomson. صفحة 346. .
- Williams, David R. (7 September 2006). "Saturn Fact Sheet". ناسا. مؤرشف من الأصل في 09 أبريل 201431 يوليو 2007.
- Showman, Adam P.; Malhotra, Renu (1999-10-01). "The Galilean Satellites" ( كتاب إلكتروني PDF ). Science. 286 (5437): 77–84. doi:10.1126/science.286.5437.77. PMID 10506564. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 5 أكتوبر 2018.
- Sohl, F.; Spohn, T; Breuer, D.; Nagel, K. (2002). "Implications from Galileo Observations on the Interior Structure and Chemistry of the Galilean Satellites". Icarus. 157 (1): 104–119. Bibcode:2002Icar..157..104S. doi:10.1006/icar.2002.6828.
- Showman, Adam P.; Stevenson, David J.; Malhotra, Renu (1997). "Coupled Orbital and Thermal Evolution of Ganymede" ( كتاب إلكتروني PDF ). Icarus. 129 (2): 367–383. Bibcode:1997Icar..129..367S. doi:10.1006/icar.1997.5778. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 3 يونيو 2019.
- Brown, D.; Anderson, J. (6 January 2011). "NASA Research Team Reveals Moon Has Earth-Like Core". NASA. ناسا. مؤرشف من الأصل في 26 ديسمبر 2018.
- Weber, R. C.; Lin, P.-Y.; Garnero, E. J.; Williams, Q.; Lognonne, P. (2011-01-21). "Seismic Detection of the Lunar Core" ( كتاب إلكتروني PDF ). Science. 331 (6015): 309–312. Bibcode:2011Sci...331..309W. doi:10.1126/science.1199375. PMID 21212323. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 15 أكتوبر 2015.
- Margot, Jean-Luc; Peale, Stanton J.; Solomon, Sean C.; Hauck, Steven A.; Ghigo, Frank D.; Jurgens, Raymond F.; Yseboodt, Marie; Giorgini, Jon D.; Padovan, Sebastiano; Campbell, Donald B. (2012). "Mercury's moment of inertia from spin and gravity data". Journal of Geophysical Research: Planets. 117 (E12): E00L09–. Bibcode:2012JGRE..117.0L09M. doi:10.1029/2012JE004161. ISSN 0148-0227.
- Aitta, A. (April 2012). "Venus' internal structure, temperature and core composition". Icarus. 218 (2): 967–974. Bibcode:2012Icar..218..967A. doi:10.1016/j.icarus.2012.01.007.
- Williams, James G. (1994). "Contributions to the Earth's obliquity rate, precession, and nutation". The Astronomical Journal. 108: 711. Bibcode:1994AJ....108..711W. doi:10.1086/117108. ISSN 0004-6256.
- Williams, James G.; Newhall, XX; Dickey, Jean O. (1996). "Lunar moments, tides, orientation, and coordinate frames". Planetary and Space Science. 44 (10): 1077–1080. Bibcode:1996P&SS...44.1077W. doi:10.1016/0032-0633(95)00154-9. ISSN 0032-0633.
- Folkner, W. M.; et al. (1997). "Interior Structure and Seasonal Mass Redistribution of Mars from Radio Tracking of Mars Pathfinder". Science. 278 (5344): 1749–1752. Bibcode:1997Sci...278.1749F. doi:10.1126/science.278.5344.1749. ISSN 0036-8075.
- Park, R. S.; Konopliv, A. S.; Bills, B. G.; Rambaux, N.; Castillo-Rogez, J. C.; Raymond, C. A.; Vaughan, A. T.; Ermakov, A. I.; Zuber, M. T.; Fu, R. R.; Toplis, M. J.; Russell, C. T.; Nathues, A.; Preusker, F. (2016-08-03). "A partially differentiated interior for (1) Ceres deduced from its gravity field and shape". Nature. 537 (7621): 515–517. Bibcode:2016Natur.537..515P. doi:10.1038/nature18955. PMID 27487219.
- Mao, X.; McKinnon, W. B. (2018). "Faster paleospin and deep-seated uncompensated mass as possible explanations for Ceres' present-day shape and gravity". Icarus. 299: 430–442. doi:10.1016/j.icarus.2017.08.033.
- Ni, D. (2018). "Empirical models of Jupiter's interior from Juno data". Astronomy & Astrophysics. 613: A32. doi:10.1051/0004-6361/201732183.
- Schubert, G.; Anderson, J. D.; Spohn, T.; McKinnon, W. B. (2004). "Interior composition, structure and dynamics of the Galilean satellites". In Bagenal, F.; Dowling, T. E.; McKinnon, W. B. (المحررون). Jupiter : the planet, satellites, and magnetosphere. New York: Cambridge University Press. صفحات 281–306. . OCLC 54081598. مؤرشف من الأصل في 2 مايو 2020.
- Fortney, J.J.; Helled, R.; Nettlemann, N.; Stevenson, D.J.; Marley, M.S.; Hubbard, W.B.; Iess, L. (6 December 2018). "The Interior of Saturn". In Baines, K.H.; Flasar, F.M.; Krupp, N.; Stallard, T. (المحررون). Saturn in the 21st Century. Cambridge University Press. صفحات 44–68. .
- McKinnon, W. B. (2015). "Effect of Enceladus's rapid synchronous spin on interpretation of Cassini gravity". Geophysical Research Letters. 42 (7): 2137–2143. doi:10.1002/2015GL063384.
- Anderson, J. D.; Schubert, G. (2007). "Saturn's satellite Rhea is a homogeneous mix of rock and ice". Geophysical Research Letters. 34 (2): L02202. Bibcode:2007GeoRL..34.2202A. doi:10.1029/2006GL028100.
- Durante, D.; Hemingway, D.J.; Racioppa, P.; Iess, L.; Stevenson, D.J. (2019). "Titan's gravity field and interior structure after Cassini". Icarus. 326: 123–132. doi:10.1016/j.icarus.2019.03.003.
- Yoder, C. (1995). Ahrens, T. (المحرر). Astrometric and Geodetic Properties of Earth and the Solar System. Washington, DC: AGU. . OCLC 703657999. مؤرشف من الأصل في 04 مارس 2016.
- Murray, Carl D.; Dermott, Stanley F. (13 February 2000). Solar System Dynamics. Cambridge: Cambridge University Press. . OCLC 40857034. مؤرشف من الأصل في 20 ديسمبر 2019.
موسوعات ذات صلة :