نظرية فسيبر (نظرية تدافع الزوج الإلكتروني في مدارات التكافؤ VSEPR من الإنجليزية: Valence shell electron pair repulsion theory) هي نموذج يستخدم في الكيمياء بغرض تعيين الشكل الهندسي الذي يتخذه جزيء على أساس عدد الألكترونات المزدوجة التي تحيط بالذرة المركزية .[1] تسمى هذه النظرية أيضا باسم مكتشفيها "نظرية غليبسي -نيهولم" ؛ حيث صاغها العالمان : "رونالد غليبسي " و" سير رونالد سيدني نيهولم".
بالنسبة إلى الاختصار VSEPR فهو ينطق بالإنجليزية ves-per"[2] أو "vuh-seh-per"[3] من بعض الكيميائيين.
يستند العالمان في نظريتهما إلى ان إلكترونات التكافؤ المزدوجة التي تحيط بذرة تتنافر عن بعضها البعض بسبب شحنتها السالبة ؛ وعلى هذا السبيل فإنهما سوف يتخذان دورانا في شكل هندسي يخفض من شدة تنافرهما ؛ بذلك يشكلان الشكل الهندسي للجزيء ككل. كما أكد "غليبسي" على أن التنافر بين إلكترونين الناشيء عن مبدأ استبعاد باولي يكون أقوى في تكوين شكل الجزيء من تاثير التنافر الإلكتروستاتيكي بينهما. [4]
تستند نظرية فسيبر على مشاهدات كثافة الإلكترونات في الجزيئات أكثر من استنادها على حسابات الدوال الموجية النظرية، وما يتعلق بها من أوربتالات ذرية هجينية.,[5]
فنظرية فسيبر هي نظرية نوعية، حيث أنها تقترح هيكلا للجزيئات يمكن تمثيله نظريا في "دالة تموضع الإلكترون" وفي نظرية الكم للذرات في الجزيئات QTAIM. [4]
نظرة عامة
تستخدم نظرية فسيبر لاستنباط توزيع الإلكترونات المزدوجة حول ذرة غير ذرة هيدروجين في جزيء، وبصفة خاصة لجزيئات بسيطة وذات تناظر symmetric molecules ، حيث تكون الذرة المركزية مشتركة في رابطات مع 2 أو أكثر من الذرات الأخرى. تشكل تلك الذرات المركزية وما يحوم حولها من إلكترونات مزدوجة - لا تشارك في الرابطة - مفتاحا لتعيين الشكل الهندسي للجزيء ككل.
يعين عدد الإلكترونات المزدوجة في غلاف إلكترونات التكافؤ في الذرة المركزية عن طريق رسم هيكل لويس للجزيء، ثم توسيعه بحيث يتضمن مجموعات الروابط الأخرى والإلكترونات المنفردة.[6] تتعامل نظرية فسيبر مع رابطة ثنائية أو رابطة ثلاثية على انها رابطة جماعية منفردة [6] . ويعرف عدد الذرات المترابطة مع الذرة المركزية وكذلك عدد الإلكترونات المنفردة المتكونة من إلكترونات تكافؤ غير مرتبطة بأنها عدد تجسيمي للذرة المركزية.
و تعتبر النظرية أن الإلكترونات المزدوجة تقع على سطح كرة حول الذرة المركزية، محاولة شغل أماكن تخفض من قوة تنافرها عن طريق توجهها إلى مواقع بعيدة عن بعضها البعض. [6][7] وبناءا على ذلك فعدد الإلكترونات المزدوجة (أو المجموعات) تحدد الشكل الهندسي الكلي للجزيء. وعلى سبيل المثال، إذا وجد اثنان من أزواج الإلكترونات يحيطون بالذرة المركزية فيكون أقل تنافر بينهم عندما يكون كل زوج على ناحية مضادة للزوج الآخر على "قطبي" الكرة. وبذلك يكون الشكل المتوقع للجزيء شكلا مستقيما . وإذا كان هناك ثلاثة أزواج من الإلكترونات المزدوجة تحيط بالذرة المركزية، فيكون أقل تنافر بينهم عندما يتخذون مواقع اطراف مثلث متساوي الأضلاع حول الذرة المركزية ؛ أي تنشأ بنية جزيئية مستوية ثلاثية. وبالمثل لأربعة أزواج إلكترونات، فيؤدون إلى أنسب هيكل في شكل رباعي الأسطح.[6]
قواعد مستنبطة من النظرية
استنبطت من نموذج فسيبر القواعد التالية للنوع AXn:[8]
- زوج الإلكترونات الخاصة بالذرة المركزية A في الجزيء يتشكل بحيث تكون المسافة بينهما أكبر ما يمكن.
- أزواج الإلكترونات الحرة (ويرمز لها بالرمز E) في الجزيء من التصنيف AXnEm يشغلون حجما أكبر من الحجم الذي تشغله زوج الإلكترونات الرابطة، وتؤدي إلى تضخيم الزاوية X-A-E وتصغير الزاوية X-A-X.
- الإلكترونات المنفردة الحرة في بقية أو بقايا تشغل احجاما أصغر مما يشغله أزواج الإلكترونات الحرة .
- وجود اختلاف كبير في الكهروسلبية بين A وX تقلل من حجم الرابطة الكيميائية.
- تحتاج الرابطة كثيرة العدد (رابطة ثنائية أو رابطة ثلاثية) إلى شغل حجم أكبر مما تحتاجة الرابطة الأحادية، حيث يتصاعد الحجم اللازم للرابطة بتصاعد رتبة الرابطة.
وبغرض تعيين البنية التقديرية لجزيء تؤخذ روابط سيغما في الحسبان فقط، أي أن الروابط المتعددة تعتبر في تلك الحالة روابط أحادية .
- الذرة المركزية الصغيرة التي تكون مرتبطة بربيطات كبيرة Ligand تؤثر على
بنيتها الإلكترونية (استقطاب) وتجعلها تحتاج إلى أحجام تزيد عن الحجم الذي يشغله زوج إلكترونات حرة.
استنباطات عند وجود أزواج إلكترونات حرة على الذرة المركزية
إذا لم تكن هناك أزواج إلكترونات حرة على الذرة المركزية يمكن ان تكون بنية الجزيء بسيطة عن طريق تعيين عدد البقايا المرتبطة بالذرة المركزية. كذلك يمكن تعيين بنية جزيء تكون فيه الذرة المركزية مرتبطة بواحد أو أكثر من أزواج الإلكترونات الحرة . فتعامل أزواج الإلكترونات الحرة معاملة البقايا المرتبطة وتميز بالرمز ψ“ . وبهذه الطريقة يصل المرء إلى "شبه هيكل" الجزيء.
مـــثال:
ذرة الأكسجين في جزيء الماء وهي الذرة المركزية ويرتبط بها 2 من ذرات الهيدروجين في رابطتين تساهميتين ، فتكون (X = 2) ولها 2 من أزواج الإلكترونات الحرة (أي أن E = 2). ومنها نحصل على العدد = 2 + 2 = 4 من "أشباه البقايا " أي شكل هيكلي شبيه برباعي السطوح، يمكن وصفه "برباعي سطوح ψ2 ".
وبتصور "اهمال " أزواج الإلكترونات الحرة وغض النظر عنهم تتبقى بنية جزيء الماء الحقيقية ذات زاوية تحددها أنوية الذرات .
مثال آخر:
نعطي هنا مثال آخر لحالة "رباعي سطوح ψ1 " يمتلك زوج إلكترونات حرة واحد، ذلك هو جزيء الأمونيا NH3.
| # | نوع الجزيء (a ) | مثال | Ψ - بنية / شبه هيكل (b ) | البنية الحقيقية (c ) | الزاوية |
|---|---|---|---|---|---|
| 1 |  AX1 |
H2 |  linear |
 خطي |
180° |
| 2 |  AX2 |
BeCl2 CO2 |
 خطي |
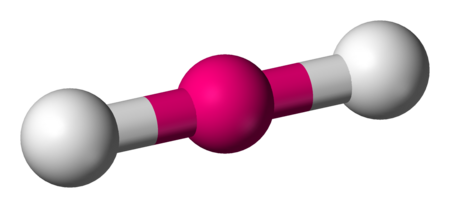 linear |
180° |
 AX1E1 |
 خطي |
 خطي |
180° | ||
| 3 | 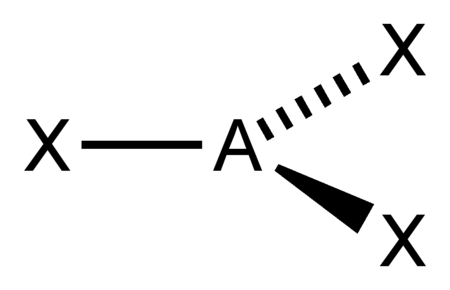 AX3 |
BF3 NO3− CO32− |
 trigonal planar |
 مثلثي مسطح |
120° |
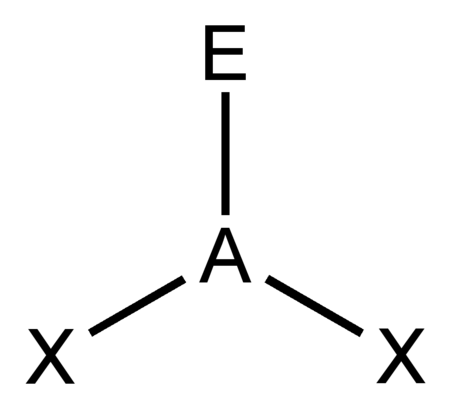 AX2E |
SO2 O3 NO2− |
 مثلثي مسطح |
 منحني |
ca. 115° | |
 AX1E2 |
 مثلثي مسطح |
 خطي |
180° | ||
| 4 |  AX4 |
CH4 SO42− PO43− ClO4− |
 tetraedrisch |
 رباعي سطوح |
109,5° |
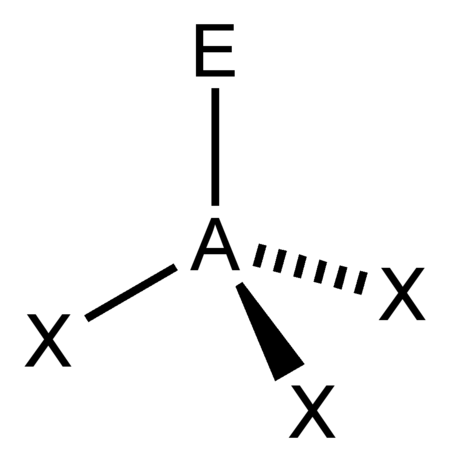 AX3E |
NH3 PCl3 |
 tetraedrisch |
 مثلثي هرمي |
ca. 107° | |
 AX2E2 |
H2O |  tetraedrisch |
 منحني |
ca. 105° | |
 AX1E3 |
HCl |  tetraedrisch |
 linear |
180° | |
| 5 |  AX5 |
PCl5 |  trigonal-bipyramidal |
 trigonal-bipyramidal |
120° / 90° |
 AX4E |
SF4, SCl4 |  trigonal-bipyramidal |
 "Wippe", bisphenoidal |
ca. 175° / 110° | |
 AX3E2 |
ClF3 |  trigonal-bipyramidal |
 T-förmig |
ca. 87,5° | |
 AX2E3 |
XeF2 |  trigonal-bipyramidal |
 linear |
180° | |
| 6 |  AX6 |
SF6 |  oktaedrisch |
 oktaedrisch |
90° |
 AX5E |
ClF5 |  oktaedrisch |
 quadratisch-pyramidal |
ca. 85° | |
 AX4E2 |
XeF4 |  oktaedrisch |
 quadratisch-planar |
90° | |
| 7 |  AX7 |
IF7 |  pentagonal-bipyramidal |
 pentagonal-bipyramidal |
90° / 72° |
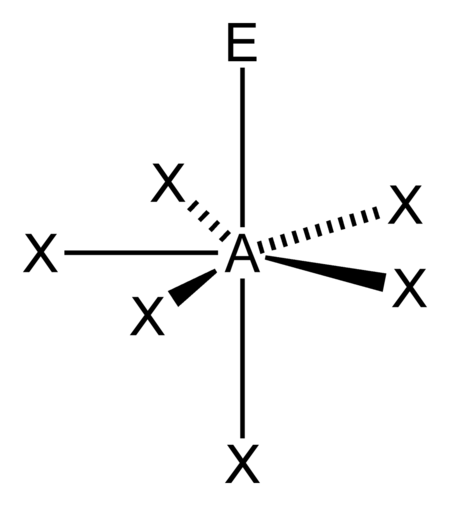 AX6E |
[XeOF5]− |  pentagonal-bipyramidal |
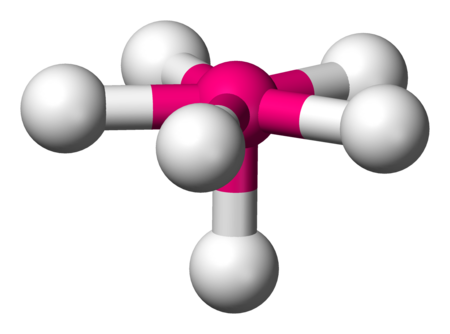 pentagonal-pyramidal |
ca. 90° / ca. 72° | |
 AX5E2 |
XeF5− |  pentagonal-bipyramidal |
 pentagonal-planar |
72° | |
| 8 | AX8 | IF8− | tetragonal-antiprismatisch | tetragonal-antiprismatisch | 78° / 73° |
ملاحظات:
- (a )
الذرة المركزية: A, بقية: X ، وزوج إلكترونات: E
- ( b )
زوج إلكترونات غير مرتبط (أصفر فاتح) ، معتبر كبقية مرتبطة
- ( c )
التوزيع الفراغي الحقيقي للذرات
مراجع
- Jolly, W. L.,Modern Inorganic Chemistry, McGraw-Hill, 1984, p.77-90.
- Petrucci R.H., Harwood W.S. and Herring F.G. General Chemistry: Principles and Modern Applications (Prentice-Hall 8th ed. 2002) p.410
- H. Stephen Stoker (2009). General, Organic, and Biological Chemistry. Cengage Learning. صفحة 119. .
- R.J. Gillespie (2008), Coordination Chemistry Reviews vol.252, pp.1315-1327, Fifty years of the VSEPR model
- Gillespie, R.J. (2004), "Teaching molecular geometry with the VSEPR model", Journal of Chemical Education, 81, صفحات 298–304, Bibcode:2004JChEd..81..298G, doi:10.1021/ed081p298
- R.H. Petrucci, W.S. Harwood and F.G. Herring, General Chemistry (8th ed., Prentice-Hall 2002) pp.410-417.
- G.L. Miessler and D.A. Tarr, Inorganic Chemistry (2nd ed., Prentice-Hall 1999) pp.54-62.
اقرأ أيضا
وصلات خارجية
- 3D Chem - Chemistry, Structures, and 3D Molecules
- IUMSC - Indiana University Molecular Structure Center

