الشبكة المنطقية

وضع مساحة شبكة منطقية مع N=4 العقد و K=1 روابط لكل عقدة. يمكن تشغيل العقد (أحمر) أو إيقاف تشغيله (أزرق). ترمز الأسهم الرفيعة (السوداء) إلى مدخلات الدالة المنطقية وهي وظيفة "نسخة" بسيطة لكل عقدة. تُظهر الأسهم السميكة (الرمادية) ما يفعله التحديث المتزامن. إجمالاً يوجد 6 (برتقالي) الجاذبينs, 4 منهم هم نقاط ثابتة.

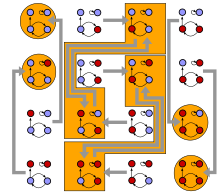
تتكون الشبكة المنطقية من مجموعة منفصلة من المتغيرات المنطقية لكل منها وظيفة منطقية (ربما تختلف عن كل متغير) مخصصة لها والتي تأخذ مدخلات من مجموعة فرعية من هذه المتغيرات والمخرجات التي تحدد حالة المتغير الذي تم تعيينه له، تحدد هذه المجموعة من الوظائف في الواقع طوبولوجيا (اتصال) على مجموعة المتغيرات، والتي تصبح بعد ذلك عُقدًا في شبكة، وعادة ما يتم أخذ ديناميكيات النظام كــ سلسلة زمنية منفصلة حيث يتم تحديد حالة الشبكة بأكملها في الوقت t +1 عن طريق تقييم وظيفة كل متغير على حالة الشبكة في الوقت t، يمكن القيام بذلك بشكل متزامن أو غير متزامن.^[1]

تم استخدام الشبكات المنطقية في علم الأحياء لنمذجة الشبكات التنظيمية، على الرغم من أن الشبكات المنطقية هي تبسيط أولي للواقع الجيني حيث لا تكون الجينات مفاتيح ثنائية بسيطة، فهناك العديد من الحالات التي تلتقط فيها بشكل صحيح النمط الصحيح للجينات المعبر عنها والمقموعة،^[2][3] لم يتم فهم النموذج الرياضي السهل (المتزامن) على ما يبدو إلا بشكل كامل في منتصف العقد الأول من القرن الحادي والعشرين.^[4]

النموذج الكلاسيكي

تعد الشبكة المنطقية نوعًا معينًا من النظام الديناميكي المتسلسل، حيث يكون الوقت والحالات منفصلة، أي أن لكل من مجموعة المتغيرات ومجموعة الحالات في السلسلة الزمنية انحيازًا إلى سلسلة صحيحة، تشبه هذه الأنظمة التشغيل الآلي الخلوي على الشبكات، باستثناء حقيقة أنه عند إعدادها، يكون لكل عقدة قاعدة يتم اختيارها عشوائيًا من بين كل 2^2K عقدة محتملة ذات مدخلات K، يميل سلوك K=2 من الفئة 2 إلى السيطرة، ولكن بالنسبة إلى K>2 ، فإن السلوك الذي يراه المرء يقترب بسرعة مما هو نموذجي لرسم الخرائط العشوائية التي ترتبط فيها الشبكة التي تمثل تطور حالات 2^N للعقد الكامنة N بشكل عشوائي.^[5]

الشبكة المنطقية العشوائية (RBN) هي شبكة يتم اختيارها عشوائيًا من مجموعة جميع الشبكات المنطقية الممكنة ذات حجم معين، N، ثم يمكن للمرء أن يدرس إحصائياً، كيف تعتمد الخصائص المتوقعة لهذه الشبكات على الخصائص الإحصائية المختلفة لمجموعة جميع الشبكات الممكنة، على سبيل المثال، يمكن للمرء أن يدرس كيف يتغير سلوك RBN مع تغير متوسط الاتصال.

تم اقتراح الشبكات المنطقية الأولى من قبل ستيوارت أ.كوفمان في عام 1969، كنماذج عشوائية للشبكات التنظيمية الجينية ^[6] ولكن فهمهم الرياضي بدأ فقط في 2000s. ^[7][8]

الجاذبون

نظرًا لأن الشبكة المنطقية لا تحتوي إلا على حالات ممكنة 2^N، فإن المسار سيصل عاجلاً أم آجلاً إلى حالة تمت زيارتها سابقًا، وبالتالي، نظرًا لأن الديناميكيات حتمية، فإن المسار سيقع في حالة ثابتة أو دورة تسمى الجاذب (على الرغم من أن دورة في المجال الأوسع من النظم الديناميكية هي فقط عامل جذب إذا الاضطرابات من ذلك يؤدي إلى العودة إليها)، إذا كان للجاذب حالة واحدة فقط، فإنه يطلق عليه الجاذب النقطي، وإذا كان الجاذب يتألف من أكثر من حالة واحدة، فيُطلق عليه الجاذب الدائري، تسمى مجموعة الحالات التي تؤدي إلى الجاذب حوض الجاذب، الدول التي لا تحدث إلا في بداية مسارات (لا مسارات تؤدي إليها)، تسمى ولايات حديقة عدن^[9] وديناميات الشبكة تتدفق من هذه الدول نحو المزارات. الوقت المستغرق للوصول إلى المزارات يسمى الوقت المؤقت.^[4]

مع تزايد قوة الكمبيوتر وزيادة فهم النموذج الذي يبدو بسيطًا، أعطى مؤلفون مختلفون تقديرات مختلفة لمتوسط عدد وطول الجاذبين، هنا ملخص موجز للمنشورات الرئيسية.^[10]

الكاتب	السنة	متوسط طول الجاذب	متوسط رقم الجاذب	التعليق
كوفمان [6]	1969	${\displaystyle \langle A\rangle \sim {\sqrt {N}}}$	${\displaystyle \langle \nu \rangle \sim {\sqrt {N}}}$
باستولا / باريسي[11]	1998	أسرع من قانون السلطة, ${\displaystyle \langle A\rangle >N^{x}\forall x}$	أسرع من قانون السلطة, ${\displaystyle \langle \nu \rangle >N^{x}\forall x}$	الأدلة الرقمية الأولى
بيلكي/ سجونسون[12]	2002		خطي مع نظام الحجم, ${\displaystyle \langle \nu \rangle \sim N}$
سوكلار/كوفمان[13]	2003		أسرع من الخطي, ${\displaystyle \langle \nu \rangle >N^{x}}$ with ${\displaystyle x>1}$
سامويلسون / تروين[14]	2003		نمو كثير الحدود, ${\displaystyle \langle \nu \rangle >N^{x}\forall x}$	البرهان الرياضي
ميهالجيف/دروسيل[15]	2005	أسرع من قانون السلطة, ${\displaystyle \langle A\rangle >N^{x}\forall x}$	أسرع من قانون السلطة, ${\displaystyle \langle \nu \rangle >N^{x}\forall x}$

تحقيق الاستقرار

في نظرية النظم الديناميكيّة، فإن تركيب وطول الجذامات في الشبكة يتوافق مع المرحلة الديناميكية للشبكة، يعتمد استقرار الشبكات المنطقية على اتصالات العقد الخاصة بها، يمكن أن تعرض الشبكة المنطقية سلوكًا مستقرًا أو هامًا أو فوضويًا، تحكم هذه الظاهرة قيمة حاسمة لمتوسط عدد اتصالات العقد (${\displaystyle K_{c}}$)، ويمكن تمييزها بمسافة هامينج كمقياس المسافة، وفي النظام غير المستقر، تنمو المسافة بين دولتين متقاربة في البداية في المتوسط على نحو مضطرد بمرور الوقت، في حين تنخفض في النظام المستقر إلى مستويات غير عادية، في هذا، مع "حالات الإغلاق الأولية"، يعني المرء أن مسافة هامينج صغيرة مقارنة بعدد العقد (${\displaystyle N}$) في الشبكة.

بالنسبة إلى نموذج N-K-model^[16] ، تكون الشبكة مستقرة إذا ${\displaystyle K<K_{c}}$ ، وحرجة إذا ${\displaystyle K=K_{c}}$ ، وغير مستقرة إذا ${\displaystyle K>K_{c}}$

يتم تحديث حالة العقدة المحددة ${\displaystyle n_{i}}$ وفقًا لــ جدول الحقيقة الخاص بها، والذي يتم تعبئة مخرجاته بشكل عشوائي، يشير ${\displaystyle p_{i}}$ إلى احتمال تعيين إخراج متوقف عن التشغيل لسلسلة معينة من إشارات الإدخال.

إذا خطأ رياضيات (خطأ في الصياغة): {\displaystyle p_{i}=p=const، } لكل عقدة، فإن الانتقال بين النطاق المستقر والفوضوي يعتمد على ${\displaystyle p}$ ، وفقًا لـ برنارد دريدا و إيف بومو^[17] ، فإن القيمة الحاسمة لمتوسط عدد الاتصالات هي ${\displaystyle K_{c}=1/[2p(1-p)]}$ .

إذا لم يكن ${\displaystyle K}$ ثابتًا، ولم يكن هناك ارتباط بين الدرجات المتدرجة والخارجة، يتم تحديد شروط الاستقرار بواسطة ${\displaystyle \langle K^{in}\rangle }$^[18][19][20] الشبكة مستقرة إذا ${\displaystyle \langle K^{in}\rangle <K_{c}}$ ، حرجة إذا ${\displaystyle \langle K^{in}\rangle =K_{c}}$ ، و  غير مستقر إذا ${\displaystyle \langle K^{in}\rangle >K_{c}}$

شروط الاستقرار هي نفسها في حالة الشبكات ذات الهيكل الخالي من المقاييس حيث يكون التوزيع داخل وخارج الدرجة توزيعًا لقانون الطاقة: ${\displaystyle P(K)\propto K^{-\gamma }}$ و ${\displaystyle \langle K^{in}\rangle =\langle K^{out}\rangle }$ ، لأن كل رابط خارجي من عقدة هو رابط داخلي لآخر.^[21]

تُظهر الحساسية احتمالية تغير ناتج الوظيفة المنطقية لعقدة معينة إذا تغير إدخالها، للشبكات المنطقية العشوائية، ${\displaystyle q_{i}=2p_{i}(1-p_{i})}$ ، في الحالة العامة، يخضع استقرار الشبكة لــ أكبر قيمة ${\displaystyle \lambda _{Q}}$ من المصفوفة ${\displaystyle Q}$ ، حيث ${\displaystyle Q_{ij}=q_{i}A_{ij}}$ ، و ${\displaystyle A}$ هي مصفوفة مجاورة للشبكة، ^[22] الشبكة مستقرة إذا ${\displaystyle \lambda _{Q}<1}$ ، حرجه إذا ${\displaystyle \lambda _{Q}=1}$ ، غير مستقرة إذا ${\displaystyle \lambda _{Q}>1}$.

اختلافات النموذج

طبولوجيا أخرى

أحد المواضيع هو دراسة طبولوجيا الرسم البياني الأساسية المختلفة.

• حالة متجانسة يشير ببساطة إلى الشبكة التي هي ببساطة تخفيض إلى نموذج إيسينج الشهير.

• يمكن اختيار طبولوجيا خالية من المقاييس للشبكات المنطقية،^[23] يمكن للمرء أن يميز الحالة التي يتم فيها توزيع التوزيع في قانون السلطة فقط، ^[24] أو فقط التوزيع خارج الدرجة أو كليهما.

مخططات التحديث الأخرى

يتم تحديث الشبكات المنطقية الكلاسيكية (تسمى أحيانًا CRBN ، أي شبكة عشوائية منطقية كلاسيكية) بشكل متزامن، وبدافع من حقيقة أن الجينات لا تغير حالتها في وقت واحد في العادة،^[25] تم تقديم بدائل مختلفة. التصنيف الشائع ^[26] هو ما يلي:

• تحديث حتمى غير متزامن

لا يتم تحديث الشبكات المنطقية (DRBNs) بشكل متزامن ولكن لا يزال هناك حل نهائي، سيتم تحديث العقدة i عندما يكون t ≡ Q_i (mod P_i) حيث t هو الوقت المحدد.^[27]

• الحالة الأكثر شيوعًا هي التحديث العشوائي الكامل (GARBN ، الشبكات المنطقية العشوائية غير المتزامنة العامة)، هنا، يتم تحديد عقدة واحدة (أو أكثر) في كل خطوة حسابية ليتم تحديثها.
• النظام الديناميكي المنطقي المرصود جزئيًا (PONDS).^{[28][29][30][31]} يختلف نموذج الإشارة عن جميع نماذج الشبكة المنطقية والعشوائية السابقة عن طريق إزالة افتراض إمكانية المراقبة المباشرة لناقل الحالة المنطقية والسماح بعدم اليقين في عملية المراقبة، معالجة السيناريو الذي واجهته في الممارسة.

تطبيق شبكات منطقية

التصنيف

تصنيف بايزي الأمثل^[32] طور تصنيفًا مثاليًا للمسارات يحسب عدم اليقين المحتمل للنموذج واقترح أيضًا تصنيف مسار قائم على الجسيمات قابل للتطوير بدرجة كبيرة للشبكات الكبيرة ذات التعقيد الأقل بكثير من الحل الأمثل.

المصادر

• Dubrova, E., Teslenko, M., Martinelli, A., (2005). *Kauffman Networks: Analysis and Applications,  in "Proceedings of International Conference on Computer-Aided Design", pages 479-484.

روابط خارجية

• DDLab
• Analysis of Dynamic Algebraic Models (ADAM) v1.1
• RBNLab
• NetBuilder Boolean Networks Simulator
• Open Source Boolean Network Simulator
• JavaScript Kauffman Network
• Probabilistic Boolean Networks (PBN)
• A SAT-based tool for computing attractors in Boolean Networks
• CoLoMoTo (Consortium for Logical Models and Tools)

موسوعات ذات صلة :

• موسوعة رياضيات