تقريب محوراني

الخطأ المتعلق بالتقريب المحورانى , فى هذه الصورة تقريب دالة جيب التمام

في علم البصريات الهندسية، يستخدم التقريب المِحورانيّ^[1] أو التقريب الموازٍ للمحور^[1] أو التقريب المجاور للمحور^[2] في بصريات غاوس وتعقب شعاع الضوء خلال نظام بصري (مثل العدسة).

• الشعاع المحوراني هو الشعاع الذي يصنع زاوية صغيرة مع المحور البصري للنظام، ويقع بالقرب من المحور خلال النظام .
• بصفة عامة، هذا يسمح لثلاثة تقريبات هامة (θ بالتقدير الدائرى ) لحساب مسار الشعاع :

${\displaystyle \sin \theta \approx \theta ,\quad \tan \theta \approx \theta \quad {\text{and}}\quad \cos \theta \approx 1.}$

• يستخدم التقريب المحورانى في بصريات غاوس و تعقب الشعاع المرفوع لأس واحد .
• تحليل مصفوفة نقل شعاع هي أحد الطرق التي تستخدم هذا التقريب .
• في بعض الحالات، فإن التقريب المرفوع لأس ${\displaystyle 2}$ يسمى (محورانى ) .
• تقريبات دالة الجيب والمماس التي بالأعلى لا تتغير بالتقريب المحورانى المرفوع لأس ${\displaystyle 2}$ (لأن الحد الثاني في متسلسلة تايلور يساوى ${\displaystyle 0}$)، بينما يتغير تقريب دالة جيب التمام المرفوعة لأس ${\displaystyle 2}$ كالتالى :

${\displaystyle \cos \theta \approx 1-{\theta ^{2} \over 2}\ .}$

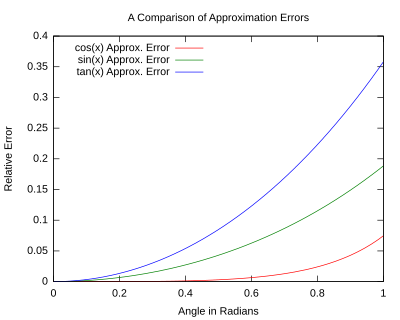
• التقريب المرفوع لأس ${\displaystyle 2}$ يكون دقيق خلال ${\displaystyle 0.5\%}$ للزوايا التي تكون تحت ${\displaystyle 10}$ درجات، لكن عدم دقته ترتفع بشكل ملحوظ مع الزوايا الكبيرة .
• بالنسبة للزوايا الكبيرة، فإنه ضرورى أن نميز بين الأشعة المتقاطعة مع المحور , والتي تقع في مستوى يحتوى على المحور البصرى , والأشعة السهمية التي لا تقع في مستوى يحتوى على المحور البصرى .

مقالات ذات صلة

• التناظر المحورى .

المصادر

• Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides 1. SPIE . pp. 19–20. رقم دولي معياري للكتاب .
• Weisstein, Eric W. (2007). "Paraxial Approximation". ولفرام ريسيرتش. ولفرام ريسيرتش. Retrieved 15 January 2014.
• "Paraxial approximation error plot". ولفرام ألفا. بحث ولفرام. Retrieved 26 August 2014.

روابط خارجية

• Paraxial Approximation and the Mirror by David Schurig, The Wolfram Demonstrations Project .

موسوعات ذات صلة :

• موسوعة الفيزياء