دالة بوليانية

في الرياضيات، الدالة البُولية هي دالة ${\displaystyle f(x)=f(x_{1},\cdots ,x_{n})}$ مع n متغيرات ${\displaystyle f:\{0,1\}^{n}\to \{0,1\}}$ نقول أنَّ f تقبل متجه ${\displaystyle a\in \{0,1\}^{n}}$ إذا 1 =(f(a ونقول انها ترفضه إذا 0 =(f(a .^[1][2][3] دالة بوليانية ليست بالضرورة متعلقة بكل متغيراتها ونقول أنَّ الدالة f متعلقة بالمتغير x_i  إذا يوجد اعداد ثابتة ${\displaystyle a_{1},\cdots ,a_{i-1},a_{i+1},\cdots ,a_{n}\in \{0,1\}}$ بحيث أنَّ:

${\displaystyle f(a_{1},\cdots ,a_{i-1},0,a_{i+1},\cdots ,a_{n})\neq f(a_{1},\cdots ,a_{i-1},1,a_{i+1},\cdots ,a_{n})}$

بما أنَّه يوجد ${\displaystyle 2^{n}}$ متجهات في ${\displaystyle \{0,1\}^{n}}$ فإن عدد الدوال البوليانية ${\displaystyle f:\{0,1\}^{n}\to \{0,1\}}$ هو ${\displaystyle 2^{2^{n}}}$.

دوال بوليانية متناظرة

دالة بوليانية نقول عنها متناظرة (symmetric) إذا اعتمدت فقط على عدد ال-1 في المُدخل وليس على مكانها اي على توزيعها على المتغيرات، لذا فانه يوجد ${\displaystyle 2^{n+1}}$ دوال كهذه، امثلة لدوال كهذه:

• دالة الحفة (threshold function) ${\displaystyle Th_{k}^{n}(x)=1\iff x_{1}+x_{2}+\cdots +x_{n}\geq k}$
• دالة الاكثرية (majority function) ${\displaystyle Maj_{n}(x)=1\iff x_{1}+x_{2}+\cdots +x_{n}\geq \left\lceil {\frac {n}{2}}\right\rceil }$
• دالة الزوجية (parity function) ${\displaystyle \oplus _{n}(x)=1\iff x_{1}+x_{2}+\cdots +x_{n}=1{\pmod {2}}}$
• دالة العد (modular function) ${\displaystyle Mod_{k}(x)=1\iff x_{1}+x_{2}+\cdots +x_{n}=0{\pmod {k}}}$

ترجمة الخصائص

يمكن ترجمة كل خاصية أو صفة إلى دالة بوليانية ملائمة وهذه الصفة يمكن ان تحقق أو لا، مثال: الصفة "العدد أولي" ملائم للدالة PRIME بحيث:

عدد اولي ${\displaystyle PRIME(x)=1\iff \sum _{i=0}^{n}x_{i}\cdot 2^{i}}$ .

ولنترجم خصائص المُخططات (graphs) على المجموعة ${\displaystyle [n]=\{1,\cdots ,n\}}$ نُعرف لكل ضلع متغير ${\displaystyle x_{ij}}$ وهذا المتغير 1 إذا ${\displaystyle (i,j)\in E(G)}$ و-0 خلاف هذا. لذا اي مُتجه قيمه 0-1 بطول ${\displaystyle {\binom {n}{2}}}$ يعطينا مُخطط G . عندها خاصية يمكن ترجمتها بشكل مناسب، بشكل عام:

خاصية مُخطط ${\displaystyle f(x)=1\iff }$

مثال:

دالة المخطط الكامل (the clique function) أو (Clique(n,k : وهذه الدالة تقبل متجه x إذا وفقط إذا G_x يحوي مخطط كامل مع k رؤوس.

مصفوفة بوليانية

مصفوفة بوليانية هي مصفوفة بحيث أنَّ كل الخلايا قيمتها اما 0 أو 1 .

إذا (f(x,y دالة بوليانية مع 2n متغيرات حينها يمكن النظر اليها على انها مصفوفة ,A, بكبر ${\displaystyle 2^{n}\times 2^{n}}$ بحيث أن كل سطر وعامود موسوم بواسطة مُتجه من ${\displaystyle \{0,1\}^{n}}$ , ويتحقق: (A[x,y]=f(x,y .

عمليات بوليانية

العمليات البوليانية الاساسية هي:

• عملية النقض (negation) ويرمز لها ب- NOT : ${\displaystyle \neg x=1-x}$ وفي بعض الاحيان: ${\displaystyle {\bar {x}}}$
• عملية الضم (conjuction) , ويرمز لها ب- AND : ${\displaystyle x\land y=x\cdot y}$
• عملية الفصل (disjunction) , ويرمز لها ب- OR : ${\displaystyle x\lor y=1-(1-y)\cdot (1-x)}$
• عملية الزوجية (parity) , ويرمز لها ب-XOR : ${\displaystyle x\oplus y=x(1-y)+y(1-x)=(x+y){\pmod {2}}}$
• عملية الاستلزام (implication) وهي ${\displaystyle x\to y=\neg x\lor y}$

من هذه العمليات يمكن تركيب دوال بوليانية أكثر تعقيدا من دوال بسيطة.

مثال:

لنفرض أنَّ ${\displaystyle f(x,y)=\neg x+(x\lor y)}$ حينها يمكن أن نبني دالة جديدة: ${\displaystyle f'(x,y,z)=\neg f(x,y)\land z}$

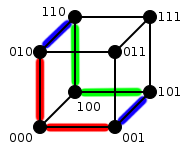
المكعب الثنائي

المعكب الثنائي هو مجموعة كل المتجهات ( اي ${\displaystyle \{0,1\}^{n}}$ ) ويمكن التعبير عنه بواسطة مُخطط (GRAPH) بحيث أنه يوجد لهذا المكعب ${\displaystyle 2^{n}}$ رؤوس وكل رأس موسوم بواسطة مُتجه(vector) من المجموعة ${\displaystyle \{0,1\}^{n}}$ ويوجد ضلع بين رأسين إذا اختلف المتجهين اللذان هما وسما الرأسين في مكان واحد. لذا فانه يوجد ${\displaystyle n\ 2^{n}}$ اضلاع في هذا المخطط، كما انَّه مخطط ثنائي . نرمز لمكعب مع ${\displaystyle 2^{n}}$ رؤوس ب- ${\displaystyle Q_{n}}$ .

A هو مُكعب جزئي بُعده d هو مجموعة شكلها كالتالي: ${\displaystyle A=A_{1}\times A_{2}\times \cdots \times A_{n}}$ بحيث أنَّ كل A_i هو أحد المجموعات: ${\displaystyle \{0\},\{1\},\{0,1\}}$ بالإضافة إلى أنه فقط ل- d من المجموعات يتحقق التالي: ${\displaystyle A_{i}=\{0,1\}}$ .

كل دالة بوليانية ${\displaystyle f:\{0,1\}^{n}\to \{0,1\}}$ يمكن النظر اليها على انها تلوين (coloring) ${\displaystyle Q_{n}}$ بلونين. المخطط الثنائي الجزئي ${\displaystyle G_{f}}$ نحصل عليه بازالة كل الاضلاع التي رؤوسها تشترك بنفس اللون. الكثافة في المخطط ${\displaystyle G_{f}}$ له فائدة في تعقيد الدوائر البوليانية للدالة f .

الاشكال الطبيعية

هنالك شكلان طبيعيان للدوال البوليانية: CNF , DNF . لعل أكثر الوسائل بديهية لتمثيل دالة بوليانية هو جدول الحقيقة الخاص بالدالة اي قائمة بكل ${\displaystyle 2^{n}}$ الازواج ${\displaystyle (a,f(a))}$ لكل ${\displaystyle a\in \{0,1\}^{n}}$ . هذه الطريقة اغلب الاحيان غير ملائمة، وسيلة أكثر ملائمة هي DNF و-CNF .

متغير بسيط (literal) هو المتغير البولياني أو ضده اي اما ان يكون ${\displaystyle x_{i}}$ أو ${\displaystyle \neg x_{i}}$. بشكل عام الترميز التالي شائع الاستخدام: ${\displaystyle x_{i}^{1}=x_{i}}$ و- ${\displaystyle x_{i}^{0}=\neg x_{i}}$ لذا فانه لكل سلسلة ${\displaystyle a=(a_{1},\cdots ,a_{n})}$ يتحقق التالي:

احادي الحدود (monomial) هو AND متغيرات بسيطة، والتعبير (clause) هو or متغيرات بسيطة. مثال:

• ${\displaystyle x\land y\land \neg z}$ هو احادي الحدود.
• ${\displaystyle x\lor y\lor \neg x\lor z}$ هو تعبير.

DNF هو OR آحاد الحدود و- CNF هو AND تعابير. كل دالة بوليانية (f(x يمكن التعبير عنها بواسطة (DNF D(x أو (CNF C(x :

ثنائي الدالة البوليانية

لكل دالة بوليانية يمكن تعريف دالة بوليانية اخرى ${\displaystyle f^{d}}$ وتسمى هذه الدالة ثنائي f . وهي كالتالي:

لهذه الدالة عدة تطبيقات بشكل طبيعي منها في نظرية التصويت (voting theory) .

لهذه الدالة كثير من الخصال منها:

لنفرض أن f,g هما دالتين بوليانيتين حينها:

1. ${\displaystyle (f^{d})^{d}=f}$
2. ${\displaystyle ({\overline {f}})^{d}={\overline {f^{d}}}}$
3. ${\displaystyle (f\lor g)^{d}=f^{d}\land g^{d}}$
4. ${\displaystyle (f\land g)^{d}=f^{d}\lor g^{d}}$
5. ${\displaystyle f\leq g\iff g^{d}\leq f^{d}}$

الدوال البوليانية على انها نظام مجموعات

لكل مجموعة جزئية S من المجموعة ${\displaystyle \{1,2,\cdots ,n\}}$ نعرف دالة التشخيص (Characteristic function) ${\displaystyle v_{S}}$ والتي تحقق:

${\displaystyle v_{S}(i)=1\iff i\in S}$

حينها يمكن تعريف الدالة البوليانية على انها علاقة (predicate) ${\displaystyle f:2^{[n]}\to \{0,1\}}$ . ويستطيع المرئ ان ينظر إلى دالة بوليانية ${\displaystyle f:2^{[}n]\to \{0,1\}}$ على انها عائلة المجموعات الجزئية التالية: ${\displaystyle {\mathcal {F}}_{f}=\{S|f(S)=1\}}$ .

دوال بوليانية احادية التوجه

لكل مُتجهين ${\displaystyle x,y\in \{0,1\}^{n}}$ نكتب ${\displaystyle x\leq y}$ إذا ${\displaystyle \forall ix_{i}\leq y_{i}}$ . دالة بوليانية احادية التوجه إذا ${\displaystyle x\leq y\Rightarrow f(x)\leq f(y)}$ . لو نظرنا ل- f على انها علاقة اي ${\displaystyle f:2^{[n]}\to \{0,1\}}$ حينها الدالة f احادية الاتجاه إذا وفقط إذا ${\displaystyle f(S)=1}$ حينها لكل ${\displaystyle S\subseteq T}$ يتحقق ${\displaystyle f(T)=1}$ .

امثلة لدوال احادية الاتجاه هي AND OR , دالة الحفة ${\displaystyle TH_{k}^{n}(x)}$ ,...

مقالات ذات صلة

المراجع

• Stasys Jukna , "Boolean Function Complexity:Advances and Frontiers", Springer

موسوعات ذات صلة :

• موسوعة فلسفة
• موسوعة تعمية
• موسوعة رياضيات
• موسوعة علم الحاسوب
• موسوعة منطق