متسلسلات Low-discrepancy

في الرياضيات, متسلسله low-discrepancy هي متسلسلة تعطي جميع قيمها N خاصية أن المتسلسلة المتفرعة x1, ..., xN، تحمل فروق منخفضة.

بصورة عامة، discrepancy لمتسلسلة ما تعتبر منخفضة إذا كانت نسبة النقاط في المتسلسلة التي تندرج تحت مجموعة ما B قريبة من النسبة ل قياس المجموعة B. تعريف discrepancy يختلف تباعاً لاختيار المجموعة B و ايضا على كيفية الطريقة المعتمدة لحساب B.  

متسلسلة low-discrepancy تسمى أيضا شبه عشوائية أو متسلسلات شبه عشوائية، بسبب كثرة استخدامها كبديل الأرقام العشوائية الموزعه توزيع موحد. مصطلح "quasi" يستخدم  للدلالة بوضوح أكثر على أن القيم المنخفضة للفروق هي ليست عشوائية ولا مزيفة، ولكن هذه المتسلسلات تتشارك بعض خواص المتغيرات العشوائية في بعض التطبيقات مثل quasi-Monte Carlo method حيث أن قيمة low-discrepancy تلعب دورا هاماً جداً.

التطبيقات

معامل الخطأ الناتج من تقديرkurtosis كدالة في عدد نقاط البيانات. القيم المضافة الشبة عشوائية تعطي اكبر قيمة للخطأ عندما c = (√5 − 1)/2. القيم العشوائية تعطي متوسط الخطأ لستة سحوبات لأرقام عشوائية، حيث أن المتوسط أخذ لتقليل من سعة الترددات.

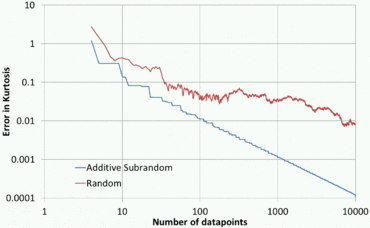
الأرقام الشبة عشوائية لديها ميزة على الأرقام العشوائية في أنها تغطي المجال تحت الدراسة بسرعة وبشكل متساو. ولديها ميزة ايضا على الاساليب الرقمية البحتة الا وهي أن الطرق الرقمية تعطي فقط دقة عالية عند عندما يكون عدد نقاط البيانات محدد مسبقاً في حين أنه عند استخدام الأرقام الشبة عشوائية الدقة تتحسن باستمرار كلما زاد عدد البيانات. من ناحية أخرى، مجموعات الأرقام الشبة عشوائية لعدد معين من النقاط تكون ذات فروقات منخفضة مقارنة بمتسلسلات الشبة عشوائية.

اثنين من التطبيقات المفيدة في العثور على الدالة المميزة من دالة الكثافة الاحتمالية في إيجاد دالة المشتقة القطعية الدالة مع كمية صغيرة من الضوضاء. الأرقام الشبة عشوائية تسمح ل اللحظات ذات القيمة العليا ان تحتسب بدقة عالية جدا بسرعة.

التطبيقات التي لا تتطلب الفرز ستكون الغاية منها هي إيجاد المتوسط, الانحراف المعياري و kurtosis للتوزيع الإحصائي وايضا في إيجاد التكامل و القيمة العظمى والصغرى للمعادلات الصعبة القطعية. الأرقام الشبة عشوائية من الممكن أن تستخدم لإيجاد نقطة انطلاق للخوارزميات القطعية التي تعمل فقط محليا، مثل نيوتن–رافسون التكرار.

الأرقام الشبة عشوائية يمكن أيضا أن تعمل جنبا إلى جنب مع خوارزميات البحث. الشجرة الثنائية لخوارزمية اسلوب فرز سريع يجب أن تعمل جيدا بشكل استثنائي لأن لأرقام الشبة عشوائية تغطي الشجرة أفضل بكثير من الأرقام العشوائية، وتجعل الشجرة تعمل بسرعه في عملية الفرز. مع خوارزمية البحث، الأرقام الشبة عشوائية يمكن استخدامها للعثور على المنوال، الوسيط, فترات الثقة و التوزيع التراكمي لتوزيع الإحصائي، و كل النقاط العظمى والصغرى وجميع الحلول للدوال القطعية.

متسلسلة low-discrepancy في التكامل العددي

على الأقل ثلاث طرق للتكامل العددي يمكن أن تصاغ على النحو التالي. بالنظر إلى مجموعة {x₁, ..., x_N} في الفترة [0,1],  القيمة التقريبية للتكامل دالة ما f هو المتوسط لقيم هذه الدالة المحسوبة عند هذه النقاط:

${\displaystyle \int _{0}^{1}f(u)\,du\approx {\frac {1}{N}}\,\sum _{i=1}^{N}f(x_{i}).}$

إذا تم اختيار النقاط على النحو x_i = i/N, فإن هذا يمثل قاعدة المستطيل. إذا تم اختيار توزيع النقاط عشوائيا (أو pseudorandomly)، فإن هذا يمثل طريقة مونت كارلو. ذا تم اختيار توزيع النقاط بحيث تكون ممثلة لعناصر متسلسلة ذات فروق منخفضة فإن هذا يمثل طريقة  quasi-Monte Carlo method. من النتائج الرائعة، أن متراجحة Koksma–Hlawka  (المذكورة أدناه) ، تنص على أن الخطأ في مثل هذا الأسلوب يمكن أن يحدد بحاضل ضرب قيمتين، واحدة تعتمد فقط على f والثانية هيا فروقات المجموعة {x₁, ..., x_N}.

من المريح بناء المجموعة {x₁, ..., x_N}  بحيث أنه إذا كانت المجموعة تتكون من N+1 عنصرفأنه من غير اللازم اعادة حساب ال N عنصر السابقين. قاعدة المستطيل تستخدم نقاط ذات فروقات منخفضة، ولكن بشكل عام العناصر يجب أن تكون يتم اعادة حسابها إذا كان العدد N تصاعدي.

في طريقة منتو كارلو العشوائية إذا كانت N تصاعدية فإنه ليس من اللازم اعادة حسابها لكن مجموعات النقاط الناتجة ليس لديها قيمة صغرى للفروقات. باستخدام متسلسلة low-discrepancy نحن نهدف لفروقات منخفضة وليس هناك حاجة لإعادة الحساب، ولكن في الواقع متسلسلة low-discrepancy يمكن أن تكون تدريجيا جيدة فيdiscrepancy إذا لم نسمح بإعادة الحساب.

تعريف discrepancy

discrepancy لمجموعة ما {P = {x1, ..., xN يمكن تعريفة باستخدام تعريف Niederreiter's كما يلي:

${\displaystyle D_{N}(P)=\sup _{B\in J}\left|{\frac {A(B;P)}{N}}-\lambda _{s}(B)\right|}$

 حيث أن λs تمثل s-بعد من قياس ليبيج،A(B;P) يمثل عدد النقاط من المجموعة P التي تقع داخل المجموعة B، ويمثل J الفترات أو المستطيلات ذات S بعد والتي يمكن كتابتها على الصورة التالية:  

${\displaystyle \prod _{i=1}^{s}[a_{i},b_{i})=\{\mathbf {x} \in \mathbf {R} ^{s}:a_{i}\leq x_{i}<b_{i}\}\,}$

حيث أن  ${\displaystyle 0\leq a_{i}<b_{i}\leq 1}$.

يمكن تعريف ال  star-discrepancy D*N بطريقة مماثلة، ماعدا ان الحد العلوي يأخذ من على المجموعة J* والتي تمثل مجموعة المستطيلات التي لها القيمة التالية

${\displaystyle \prod _{i=1}^{s}[0,u_{i})}$

حيث أن u_i   تمثل الفترة النصف مفتوحة [0, 1).

التعريفين السابقين مرتبطين بالمتراجحة التالية

${\displaystyle D_{N}^{*}\leq D_{N}\leq 2^{s}D_{N}^{*}.\,}$

 متراجحة Koksma–Hlawka 

لتكن  Īs مكعب الوحدة ذو s بعد حيث  Īs = [0, 1] × ... × [0, 1]. ولتكن لـ f حدود bounded variation في مكعب الوحدة  Īs تحت شروط  Hardy and Krause. إذن لكل x1, ..., xN في Is = [0, 1) × ... × [0, 1), تحقق أن 

${\displaystyle \left|{\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f(u)\,du\right|\leq V(f)\,D_{N}^{*}(x_{1},\ldots ,x_{N}).}$

متراجحة  Koksma–Hlawka متحققة في حالة أن: لكل مجموعة نقاط {x1,...,xN} داخل مكعب الوحدة  Īs و لأي  ${\displaystyle \varepsilon >0}$

${\displaystyle \left|{\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f(u)\,du\right|>D_{N}^{*}(x_{1},\ldots ,x_{N})-\varepsilon .}$

لذلك، جودة قاعدة التكامل العددي تعتمد على ال discrepancy D*N(x1,...,xN).

 صيغة Hlawka–Zaremba

Let ${\displaystyle D=\{1,2,\ldots ,d\}}$. For ${\displaystyle \emptyset \neq u\subseteq D}$ we write

${\displaystyle dx_{u}:=\prod _{j\in u}dx_{j}}$

حيث يرمز بـ${\displaystyle (x_{u},1)}$ للنقاط التي تم الحصول عليها من x وذلك باستبدال الاحداثيات في u بـ 1. لذلك

${\displaystyle {\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f(u)\,du=\sum _{\emptyset \neq u\subseteq D}(-1)^{|u|}\int _{[0,1]^{|u|}}\operatorname {disc} (x_{u},1){\frac {\partial ^{|u|}}{\partial x_{u}}}f(x_{u},1)\,dx_{u},}$

حيث أن ${\displaystyle \operatorname {disc} (z)={\frac {1}{N}}\sum _{i=1}^{N}\prod _{j=1}^{d}1_{[0,z_{j})}(x_{i,j})-\prod _{j=1}^{d}z_{i}}$ يمثل دالة ال discrepancy.

The ${\displaystyle L^{2}}$ version of the Koksma–Hlawka inequality

تطبيق المتراجحة  Cauchy–Schwarz inequality على التكاملات و جمعها بحسب Hlawka–Zaremba يعطينا تعريف لل L^{2} للمتراجحة Koksma–Hlawka inequality:

${\displaystyle \left|{\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f(u)\,du\right|\leq \|f\|_{d}\operatorname {disc} _{d}(\{t_{i}\}),}$

حيث

${\displaystyle \operatorname {disc} _{d}(\{t_{i}\})=\left(\sum _{\emptyset \neq u\subseteq D}\int _{[0,1]^{|u|}}\operatorname {disc} (x_{u},1)^{2}\,dx_{u}\right)^{1/2}}$

and

${\displaystyle \|f\|_{d}=\left(\sum _{u\subseteq D}\int _{[0,1]^{|u|}}\left|{\frac {\partial ^{|u|}}{\partial x_{u}}}f(x_{u},1)\right|^{2}dx_{u}\right)^{1/2}.}$

متراجحة Erdős–Turán–Koksma

أنه من الصعب حاسوبيا ايجاد القيمة الصحيحة لل discrepancy لعدد كبير من نقاط المجموعات، لكن متراجحة Turán–Koksma تعطي تعريف للحد العلوي 

Let x₁,...,x_N be points in I^s and H be an arbitrary positive integer. Then

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\leq \left({\frac {3}{2}}\right)^{s}\left({\frac {2}{H+1}}+\sum _{0<\|h\|_{\infty }\leq H}{\frac {1}{r(h)}}\left|{\frac {1}{N}}\sum _{n=1}^{N}e^{2\pi i\langle h,x_{n}\rangle }\right|\right)}$

حيث

${\displaystyle r(h)=\prod _{i=1}^{s}\max\{1,|h_{i}|\}\quad {\mbox{for}}\quad h=(h_{1},\ldots ,h_{s})\in \mathbb {Z} ^{s}.}$

بناء متسلسلات  low-discrepancy

لأن كل توزيع للأرقام العشوائية من الممكن عمل راسم له لتوزيع موحد، و ايضا الارقام الشبة عشوائية من الممكن عمل راسم لها بنفس الطريقة، هذه المقالة تهتم فقط بـ انتاج نقاط شبة عشوائية في توزيع محدد  متعدد الابعاد  

من الممكن كتابة بناء المتسلسلة على الشكل التالي

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\leq C{\frac {(\ln N)^{s}}{N}}.}$

حيث أن C هو ثابت ما يعتمد على المتسلسلة. الامثلة في الأسفل هيا أمثلة لـ  van der Corput sequence، Sobol sequences.

الأرقام العشوائية

من الممكن توليد متسلسلات للآرقام الشبة عشوائية من أرقام عشوائية وذلك باستخدام ترابط عكسي بين هذه الارقام العشوائية. آحد الطرق هي بالبدأ بمجموعة من الارقام العشوائية r_{i} في الفترة [0,0.5) وبعد ذلك يتم بناء الارقام الشبة عشوائية s_{i} حيث أنها موحدة داخل الفترة [0,1) باستخدام  

${\displaystyle s_{i}=r_{i}}$ for ${\displaystyle i}$ odd and ${\displaystyle s_{i}=0.5+r_{i}}$ for ${\displaystyle i}$ even.

طريقة اخرى هي باستخدام أرقام عشوائية لبناء سير عشوائي بمقدار خطوة 0.5 كما يلي:

${\displaystyle s_{i}=s_{i-1}+0.5+r_{i}{\pmod {1}}.\,}$

لبناء هذه المتسلسلات في أكثر من بعد، نستخدم Latin squares للبعد المراد ايجادة وذلك لضمان ان المجال تم تغطيته بشكل متساو

تغطية النقاط لوحدة المربع. اليسار مثال على أرقام شبة عشوائية بثابت c يساوي 0.5545497..., 0.308517. اليمين يمثل الارقام العشوائية من فوق لتحت 10, 100, 1000,10000

موسوعات ذات صلة :

• موسوعة رياضيات