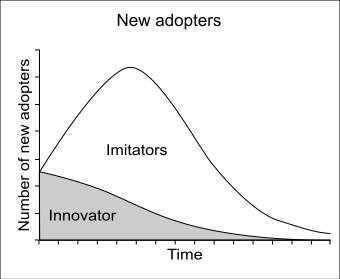
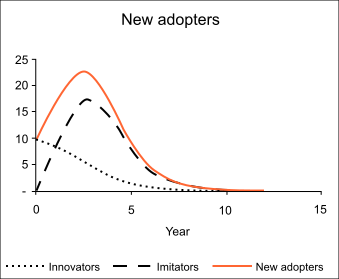
نموذج انتشار باس

نموذج انتشار باس هو نموذج ابتكره فرانك باس حيث وصف كيفية الحصول على منتجات جديدة نتيجة للتفاعل بين المستخدمين والمستخدمين المحتملين. وقد وُصفت بأنها واحدة من التعميمات التجريبية الأكثر شهرة في مجال التسويق، إلى جانب نموذج دركليه لإعادة شراء واختيار العلامة التجارية.^[1] وهذا النموذج مُستخدم على قطاع واسع في التنبؤ، وبخاصة في التنبؤ بالمنتجات والتنبؤ بالتكنولوجيا. ورياضيًا، يُعد انتشار باس الرئيسي هو معادلة ريكاتي (Riccati) ذات المُعاملات الثابتة.

نشر فرانك باس بحثة "النموذج الجديد لزيادة منتجات السلع الاستهلاكية المعمرة" في عام 1969.^[2] وقبل ذلك نشر إيفرت روجرز (Everett Rogers) انتشار المبتكرات، وهو عمل مهم للغاية وصف المراحل المختلفة لاعتماد المنتَج. وساهم باس ببعض أفكاره الرياضية في هذا المفهوم.^[3]

حيث كان لهذا النموذج تأثير كبير في التسويق وعلم الإدارة. وفي عام 2004 تم اختياره كواحد من الأبحاث العشرة الأكثر أهمية على مدار 50 عامًا من التاريخ في علم الإدارة.^[4] It was ranked number five, and the only marketing paper in the list. وقد أُعيدت طباعته بعد ذلك في العدد الصادر في ديسمبر 2004 عن علم الإدارة.^[4]

صياغة النموذج

${\displaystyle {\frac {f(t)}{1-F(t)}}=p+qF(t)}$ ^[2]

حيث:

• amp;lt;math>\ f(t) </math> هو معدل التغير في كسر القاعدة المركبة.
• ${\displaystyle \ F(t)}$ هو كسر القاعدة المركبة.
• ${\displaystyle \ p}$ هو مُعامل الابتكار.
• ${\displaystyle \ q}$ هو مُعامل التقليد.

في حين أن مبيعات ${\displaystyle \ S(t)}$ هو معدل التغير في (اعتماد) القاعدة المركبة ${\displaystyle \ f(t)}$ مضروبًا في الاحتمالات السوقية النهائية ${\displaystyle \ m}$:

${\displaystyle \ S(t)=mf(t)}$

${\displaystyle \ S(t)=m{\frac {(p+q)^{2}}{p}}{\frac {e^{-(p+q)t}}{(1+{\frac {q}{p}}e^{-(p+q)t})^{2}}}}$ ^[2]

ويعتبر وقت ذروة مبيعات هو ${\displaystyle \ t^{*}}$

${\displaystyle \ t^{*}={\frac {\ln q-\ln p}{p+q}}}$ ^[2]

الشرح

يُعرف المُعامل p بمعامل الابتكار أو التأثير الخارجي أو تأثير الإعلان عن السلع. بينما يُعرف المُعامل "q" بمُعامل التقليد أو التأثير الداخلي أو تأثير الإشاعات.

وتُحدد القيم النموذجية للمُعاملين p وq عندما يُقاس الزمن t بالسنوات:^[5]

• وقد وُجد أن قيمة p المتوسطة تساوي 0.03 وغالبًا ما تكون أقل من 0.01.
• بينما وُجد أن القيمة المتوسطة لـ q تساوي 0.38، في المدى المثالي بين 0.3 و0.5.

امتدادات النموذج

نموذج باس العمومي (بالتسعير)

وجد باس أن نموذجه هذا يتوافق مع بيانات جميع مقدمات المنتجات تقريبًا، بصرف النظر عن المجموعة الواسعة من متغيرات القرار الإداري، على سبيل المثال عملية التسعير والإعلان عن السلع. وهذا يعني أن متغيرات القرار يمكنها تحويل منحنى باس في الوقت المحدد، لكن شكل هذا المنحنى لا يطرأ عليه أي تغيير.

ورغم طرح العديد من امتدادات النموذج، فإن أحد هذه الامتدادات يُختزل إلى نموذج باس في الظروف العادية.^[4] وقد طور فرانك باس وتريشي كريشنان وديباك جاين هذا النموذج في عام 1994:

${\displaystyle {\frac {f(t)}{1-F(t)}}=(p+{q}F(t))x(t)}$

حيث إن ${\displaystyle \ x(t)}$ هي دالة نسبة التغير في السعر والمتغيرات الأخرى.

الأجيال المتتالية

تتوالى المنتجات التكنولوجية واحدًا تلو الآخر في الأجيال. قام كل من نورتون وباس بمد هذا النموذج في عام 1987 لتدعيم مبيعات المنتجات التي تتمتع بعمليات شراء مستمرة. وتتم صياغة الأجيال الثلاثة على النحو التالي:^[4]

${\displaystyle \ S_{1,t}=F(t_{1})m_{1}(1-F(t_{2}))}$

${\displaystyle \ S_{2,t}=F(t_{2})(m_{2}+F(t_{1})m_{1})(1-F(t_{3}))}$

${\displaystyle \ S_{3,t}=F(t_{3})(m_{3}+F(t_{2})(m_{2}+F(t_{1})m_{1}))}$

حيث إن

• ${\displaystyle \ m_{i}=a_{i}M_{i}}$
• ${\displaystyle \ M_{i}}$ هو العدد التزايدي للمتبنين النهائيين للمنتج المنتمي إلى الجيل i
• amp;lt;math>\ a_i </math> هو المتوسط (المستمر) لتكرار معدل الشراء بين المتبنين للمنتج المنتمي إلى الجيل i.
• ${\displaystyle \ t_{i}}$ هو الوقت المستغرق منذ بدء العمل في إنتاج المنتج المنتمي إلى الجيل i.
• ${\displaystyle \ F(t_{i})={\frac {1-e^{-(p+q)t_{i}}}{1+{\frac {q}{p}}e^{-(p+q)t_{i}}}}}$

وقد وُجد أن مدة كل من "p" و"q" عادةً ما تكون متساوية بين الأجيال المتعاقبة.

العلاقة مع منحنيات- s الأخرى

هناك نوعان من الحالات الاستثنائية لنموذج انتشار باس.

• تحدث الحالة الاستثنائية الأولى عندما تكون q=0، وذلك عندما يُختزل النموذج إلى التوزيع الأسي.
• بينما تُختزل الحالة الاستثنائية الثانية إلى التوزيع المنطقي، عندما تكون p=0.

لذا يعتبر نموذج باس حالة استثنائية من جاما/توزيع جومبرتز المتغير (جاما/جومبرتز المتغير).

الاستخدام في الشبكات الاجتماعية على الإنترنت أدى النمو السريع والحديث (اعتبارًا من أوائل عام 2007) في الشبكات الاجتماعية على الإنترنت (وغيرها من المجتمعات الافتراضية) إلى زيادة استخدام نموذج انتشار باس. ويُستخدم نموذج انتشار باس لتقييم الحجم ومعدل نمو هذه الشبكات الاجتماعية.

مقالات ذات صلة

• انتشار المبتكرات
• التنبؤ
• توزيع جومبرتز المتغير
• نموذج المستخدم الخمول

المراجع

وصلات خارجية

• Frank M. Bass Official Website

موسوعات ذات صلة :

• موسوعة إدارة أعمال