الرئيسيةعريقبحث

وحدة فلكية

☰ جدول المحتويات

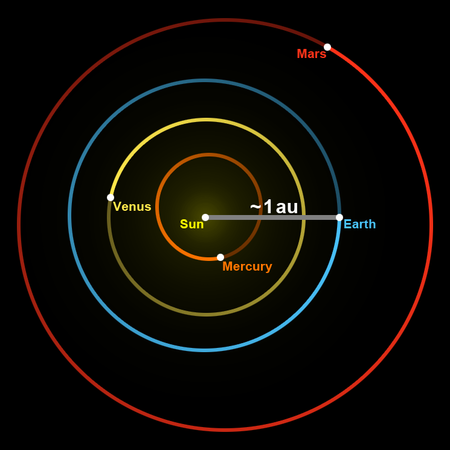
الوحدة الفلكية يرمز لها «و.ف» (Astronomical unit يرمز لها au)‏ وحدة يقاس بها غالبًا بعد الكواكب عن الشمس وهي تساوي متوسط بعد الأرض عن الشمس، ولكن تختلف هذه المسافة مع دوران الأرض في مدارها حول الشمس إذ تكون الأرض عند أبعد مسافة لها عن الشمس مرةً في السنة عند نقطة الأوج الشمسي، ثم تقترب من الشمس مرةً أخرى خلال مدارها حتى تصل إلى أقرب مسافة لها من الشمس عند نقطة الحضيض الشمسي. وُضعت هذه الوحدة في الأصل على أنها متوسط مسافة الأوج والحضيض الشمسي، إذ حُددت الوحدة الفلكية منذ عام 2012 على أنها مسافة تبلغ 1.495978707×1011 متر، أو 150 مليون كيلومتر تقريبًا. تستخدم الوحدة الفلكية بشكل رئيسي في قياس المسافات ضمن النظام الشمسي أو المسافات الخاصة بالنجوم الأخرى. وتعتبر أيضًا عنصرًا رئيسيًا في تحديد وحدة أخرى لقياس المسافات الفلكية تعرف بالفرسخ الفلكي.

وحدة فلكية
Astronomical unit.png
 
النوع وحدة مسافة[1]،  ووحدات يمكن استخدامها مع النظام الدولي للوحدات 
تستخدم لقياس طول[2][1] 
رمز الوحدة (بالروسية: а.е.)‏،  و(بالتترية: а.б.)‏،  و(AU)‏،  و(ua)‏[2][1]،  و(au)‏،  و(بالفنلندية: au)‏،  و(بالكتالونية: UA)‏ 
تحويلات الوحدة
إلى النظام الدولي 149597870700 متر[2][1] 

تعريف الوحدة الفلكية

تمثل الوحدة الفلكية (رمزها و.ف.) متوسط المسافة بين الأرض والشمس.

قيمتها الحالية

الوحدة الفلكية هي متوسط المسافة بين الأرض والشمس والتي تساوي 149.597.870,691 كيلومتر (بدقة ± 3 مترا) أي أن:

لكن العامة تعتبر أن قيمة الوحدة الفلكية تساوي تقريبًا 150.000.000 كيلومترا وهي قيمة أسهل حفظًا لكن القيمة الحقيقية أصغر بـ 402129.309 كيلومترا ولا يمكننا اعتبار 402130 كيلومترا قيمة يمكننا تجاهلها!.

استخداماتها

بدأ استخدامها منذ عام 1958م للتعبير عن المسافة بين الكواكب والشمس وباقي المسافات داخل النظام الشمسي أو داخل باقي النظم الكوكبية لأنه بالرغم من كبرها فهي ليست عملية لقياس المسافات بين النجوم مثلا حيث تستعمل وحدة السنة الضوئية.

متوسط المسافة بين كواكب المجموعة الشمسية والشمس بالوحدة الفلكية

مسافات أخرى عن الشمس

تاريخ

يوضح كتاب عن حجم ومسافة الشمس والقمر المنسوب لعالم الفلك أرسطرخس أنه أجرى حسابات على مسافة الشمس من الأرض، وقدّر أنها تتراوح بين 18 إلى 20 مرة مسافة القمر من الأرض تقريبًا، بينما كانت النسبة الصحيحة بين المسافتين هي 389.174. اعتمد هذا التقدير على الزاوية بين القمر في طوره النصفي والشمس، والتي قدّرها أرسطرخس بنحو 87 درجة (وكانت الزاوية الصحيحة تقترب من 89.853 درجة). وفقًا لمسافة القمر من الأرض التي افترض فان هيلدن أن أرسطرخس استخدمها، افترضت حسابات أرسطرخس لمسافة الشمس أنها سوف تكون على مسافة تساوي نصف قطر الأرض بنحو 380 إلى 1520 مرة.[5]

بينت مخطوطة رياضياتية صينية قديمة يرجع تاريخها للقرن الأول قبل الحقبة العامة، وعُرفت باسم «تشوبي سوان شينغ» أن المسافة بين الأرض والشمس يمكن حسابها هندسيًا، وذلك باستخدام قياس الأطوال المختلفة للظلال التي تُرصد بمواقع مختلفة يبعد كل منها عن الآخر بمسافة 1000 ميل صيني، وهذا بافتراض أن الأرض مسطحة.[6]

قدّر بطليموس متوسط مسافة الشمس من الأرض بأنها مساوية لنصف قطر الأرض بنحو 1210 مرة،[7][8] وذلك في القرن الثاني من الحقبة العامة. بدأ بطليموس أولًا بقياس تزيح القمر ليتوصل لهذا التقدير، ووجد أن التزيح الأفقي للقمر يبلغ درجة و26 دقيقة، والذي اعتُبر كبيرًا للغاية. استنتج بطليموس بعدها أن أقصى مسافة للقمر من الأرض تساوي نصف قطر الأرض بنحو 64.17 مرة. ويمكن اعتبار استنتاج بطليموس صحيحًا تقريبًا،[9][10] وذلك بعد إلغاء الأخطاء الموجودة بقياسه لتزيح القمر، ونظريته لمدار القمر، وبعض العوامل الأخرى. أجرى بطليموس بعد ذلك قياسات على حجمي الشمس والقمر الظاهرين واستنتج أن القطر الظاهر للشمس يساوي تقريبًا القطر الظاهر للقمر عندما يكون في مسافته القصوى من الأرض، واستخدام بطليموس السجلات الخاصة بحالات الكسوف ليتوصل لهذا الاستنتاج، وتوصل أيضًا من خلالها إلى استنتاج القطر الظاهر للظل المخروطي للأرض الذي يعبر القمر من خلاله أثناء الكسوف القمري. ويمكن حساب المسافة بين الشمس والأرض باستخدام هذه المعطيات من خلال حساب المثلثات، والذي بيّن أنها تساوي نصف قطر الأرض بنحو 1210 مرة. وتبلغ نسبة مسافة الشمس إلى مسافة القمر من الأرض 19 تقريبًا وفقًا لحسابات بطليموس، ويتوافق هذا مع حسابات أرسطرخس. وبالرغم من أن الطريقة الحسابية التي استخدمها بطليموس فعالة من الناحية النظرية، فإنها تعتبر حساسة للغاية لأي تغيرات طفيفة في البيانات، إذ إن تغيير القياسات ببضع درجات مئوية يمكن أن يجعل مسافة الشمس كبيرةً بشكل لا نهائي.[9]

أجرى علماء الفلك بعض التعديلات على النموذج الكوني لبطليموس بعد انتقال علم الفلك من الحضارة اليونانية إلى الحضارة الإسلامية القروسطية، ولكن لم يغيروا العلماء وقتها من مسافة الشمس التي حسبها بطليموس بشكل كبير. فعلى سبيل المثال، وضح أحمد بن كثير الفرغاني في مقدمته عن علم الفلك البطلمي أن المسافة الشمسية تساوي نصف قطر الأرض بنحو 1170 مرة، بينما استخدم محمد بن جابر بن سنان البتاني مسافة شمسية في زيجه الفلكي مساوية لنصف القطر الأرض بنحو 1108 مرة. استخدم علماء الفلك اللاحقون مثل أبو الريحان البيروني قيم مشابهة لهذه المسافات.[11] وفي أوروبا فيما بعد، استخدم كل من كوبرنيكوس وتيخو براهي أيضًا قيم مشابهة للمسافة الشمسية، والتي تساوي نصف قطر الأرض بنحو 1142 و1150 مرة، لهذا ظلت حسابات بطليموس للمسافة بين الأرض والشمس باقيةً حتى القرن السادس عشر.[12]

كان يوهانس كيبلر أول من أدرك أن حسابات بطليموس أقل من المسافة الشمسية الحقيقية (بنحو ثلاث مرات على الأقل) وفقًا لما وضحه في كتابه جداول رودولفين عام 1627. ساعدت قوانين كيبلر للحركة الكوكبية علماء الفلك على حساب المسافات النسبية للكواكب من الشمس، وحساب المسافة المطلقة للأرض من الشمس (والتي يمكن تطبيقها على بقية الكواكب بعد حسابها). وساعد اختراع التلسكوب على إجراء القياسات الدقيقة الخاصة بالزوايا، والتي تعجز العين المجردة عن تحديدها بدقة. كرر عالم الفلك البلجيكي غودفروا فيندلين قياسات أرسطرخس عام 1635، ووجد أن مسافة الشمس الخاصة ببطليموس أقل من المسافة الحقيقية بنحو 11 مرة.

التطورات

يمكن التعبير عن وحدة المسافة A (قيمة الوحدة الفلكية بالمتر) باستخدام الثوابت الفلكية الأخرى:

يعبر G عن ثابت الجاذبية لنيوتن، ويعبر☉M عن كتلة الشمس، ويعبر k عن القيمة العددية لثابت الجذب لغاوس، ويعبر D عن الفترة الزمنية لليوم الواحد. وتفقد الشمس كتلتها بصورة ثابتة بفعل انبعاث الطاقة منها بشكل مستمر، ولهذا تتسع مدارات الكواكب إلى الخارج بعيدًا عن الشمس بشكل منتظم بمرور الوقت. وأدى هذا إلى دعوات بالتوقف عن استخدام الوحدة الفلكية باعتبارها وحدة قياس ثابتة للمسافات.[13][14]

اقترحت دراسة تحليلية لقياس الإشعاع بالنظام الشمسي الداخلي عام 2004 أن الزيادة القرنية في وحدة المسافة كانت أكبر بكثير عما يمكن أن تسببه الانبعاثات الإشعاعية الشمسية، بواقع زيادة في المسافة تصل إلى 15 ±4 متر خلال القرن الواحد.[15][16]

لم تؤكَد قياسات التغيرات القرنية في الوحدة الفلكية بواسطة بقية العلماء، وظلت هذه القضية جدلية حتى الآن. ومن ناحية أخرى، لم تستخدم الوحدة الفلكية في التقويم الفلكي الكوكبي منذ عام 2010.[17]

انظر أيضُا

مراجع

  1. العنوان : Quantities and units—Part 3: Space and time — الاصدار الأول — الباب: 3-1.C.b — الناشر: المنظمة الدولية للمعايير
  2. العنوان : Quantities and units—Part 1: General — الاصدار الأول — الباب: 6.5.6 — الصفحة: 22 — الناشر: المنظمة الدولية للمعايير
  3. http://www.iau.org/public/measuring - تصفح: نسخة محفوظة 05 يونيو 2013 على موقع واي باك مشين.
  4. Thérèse Encrenaz et alii, Le Système solaire, éd. EDP/CNRS, 2003, صفحة 274, تصفح الكتاب عبر النت (نسخة فرنسية) - تصفح: نسخة محفوظة 29 أبريل 2014 على موقع واي باك مشين.
  5. Van Helden, Albert (1985), Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley, Chicago: University of Chicago Press, صفحات 5–9,  
  6. Lloyd, G.E.R. (1996), Adversaries and Authorities: Investigations into Ancient Greek and Chinese Science, Cambridge University Press, صفحات 59–60,  
  7. Goldstein, Bernard R. (1967), "The Arabic Version of Ptolemy's Planetary Hypotheses", Trans. Am. Phil. Soc., 57 (4): 9–12, doi:10.2307/1006040, JSTOR 1006040
  8. van Helden, Albert (1985), Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley, Chicago: University of Chicago Press, صفحات 15–27,  
  9. pp. 16–19, van Helden 1985
  10. p. 251, Ptolemy's Almagest, translated and annotated by G.J. Toomer, London: Duckworth, 1984, (ردمك )
  11. pp. 29–33, van Helden 1985
  12. pp. 41–53, van Helden 1985
  13. Noerdlinger, Peter D. (2008), "Solar Mass Loss, the Astronomical Unit, and the Scale of the Solar System", Celestial Mechanics and Dynamical Astronomy, 0801: 3807, arXiv:, Bibcode:2008arXiv0801.3807N
  14. "AU may need to be redefined", New Scientist, 6 February 2008, مؤرشف من الأصل في 28 أبريل 2015
  15. Krasinsky, G.A.; Brumberg, V.A. (2004), "Secular increase of astronomical unit from analysis of the major planet motions, and its interpretation", Celestial Mechanics and Dynamical Astronomy, 90 (3–4): 267–88, Bibcode:2004CeMDA..90..267K, doi:10.1007/s10569-004-0633-z
  16. John D. Anderson & Michael Martin Nieto (2009), "Astrometric Solar-System Anomalies;§ 2: Increase in the astronomical unit", American Astronomical Society, 261, صفحات 189–97, arXiv:, Bibcode:2009IAU...261.0702A, doi:10.1017/s1743921309990378
  17. Fienga, A.; et al. (2011), "The INPOP10a planetary ephemeris and its applications in fundamental physics", Celestial Mechanics and Dynamical Astronomy, 111 (3): 363, arXiv:, Bibcode:2011CeMDA.111..363F, doi:10.1007/s10569-011-9377-8

موسوعات ذات صلة :