Obliquité
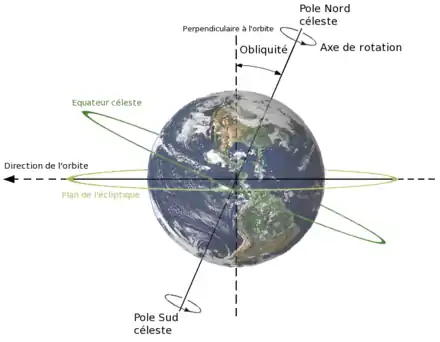
L'inclinaison de l'axe ou obliquité est une grandeur qui donne l'angle entre l'axe de rotation d'une planète (ou d'un satellite naturel d'une planète) et une perpendiculaire à son plan orbital.
Caractéristiques
Dans le système solaire, les planètes ont des orbites qui se situent toutes à peu près dans le même plan. Le plan de l'orbite de la Terre autour du Soleil est appelé l'écliptique. Chaque planète tourne en outre autour de son axe de rotation, phénomène à l'origine de la succession des jours locaux de chaque planète. Cet axe de rotation n'est jamais perpendiculaire au plan orbital de la planète, mais incliné d'un certain angle, très variable suivant les planètes du système solaire. Toujours suivant les planètes, cet axe est soumis au phénomène de la précession, de façon plus ou moins marquée. Mais en première approximation, cet axe de rotation garde à court terme une direction fixe dans l'espace.
Dans le cas de la Terre, cet angle était, en appliquant la formule de long terme de Laskar (1986), de 23° 26′ 11,150″ (ou 23,4364305466°) au [1],[2]. Cet angle s'inscrit à 23° 26′ 10,682″ (ou 23.4363006104°) au . A noter que cette donnée ne tient pas compte de la nutation, dont l'angle était de +4,081″ au et de +6,549″ au . On parle plus couramment de l'inclinaison de l'écliptique sur le plan de l'équateur. Par simplification de langage, on assimile parfois inclinaison de l'axe et inclinaison de l'écliptique. On parle aussi d'obliquité de l'écliptique, obliquité « moyenne » (ε๐) si on ne tient pas compte de la nutation et obliquité « vraie » (ε) si on en tient compte, avec ε = ε๐ + Δε, où Δε est la nutation en obliquité. Ainsi, au , l'obliquité moyenne, selon Laskar (1986), était de 23° 26′ 11,150″ et l'obliquité vraie de 23° 26′ 15,231″ ; toujours au , selon le modèle P03 (2003) recommandé depuis 2006 par l'UAI et l'IMCCE, l'obliquité moyenne était de 23° 26′ 11,084″ et l'obliquité vraie de 23° 26′ 15,165″. Au 1er janvier 2023, les valeurs Laskar (1986) sont de respectivement 23° 26′ 10,682″ et 23°. Pour le modèle P03 (2003), les valeurs correspondantes à cette même date s'élèvent à respectivement 23° 26′ 10,634″ et 23° 26′ 17,183″.
Du fait de la précession, l'inclinaison de l'axe de la Terre perd de nos jours environ 46,806″ par siècle julien (du 1.1.2023 au 2.1.2123), selon le modèle Laskar (1986), ou 46,833″, selon le modèle P03 (2003), plus largement admis aujourd'hui par la communauté scientifique.
Selon Ptolémée, ce fut Ératosthène (v. 276 - v.194 av. J.-C.) qui, le premier, démontra l'inclinaison de l'écliptique sur l'équateur[3]. Il établit sa valeur à 23° 51′. Mais Pythéas avait déjà effectué ces calculs presque un siècle avant grâce à ses mesures faites à Marseille[4] et validées par l'observation du soleil de minuit au-delà du cercle polaire lors de son expédition vers 325 à 300 av. J.-C. L'astronome danois Tycho Brahe la détermina en 1587 à 23° 30′ 30″. Il la réévalua en 1590 à 23° 29′ 46″[5].
Conséquences
C'est l'existence et le maintien de cette inclinaison naturelle qui entraînent, par le déplacement de la planète sur son orbite, la succession des saisons. Ainsi, pour la Terre, de mars à septembre, la partie nord du globe voit le Soleil plus haut à midi dans le ciel que la partie sud, et c'est l'été dans l'hémisphère Nord. Comme les rayons solaires arrivent sur Terre avec un angle plus proche de 90°, une même unité de surface reçoit plus de rayons lumineux qu'à midi dans le sud à la même époque. Du fait de cette inclinaison, le Soleil se lève plus tôt, se couche plus tard, et les jours sont de fait plus longs. Les rayons solaires dans l'hémisphère Sud sont beaucoup plus inclinés et arrosent une plus grande surface, ils distribuent donc moins de chaleur par unité de surface : c'est l'hiver. Le Soleil paraît aussi plus bas sur l'horizon et les jours sont plus courts, avec un astre qui se lève plus tard et se couche plus tôt. Ces effets sont d'autant plus prononcés que la latitude de l'observateur est grande. À l'équateur, l'effet est d'ailleurs très faible, et la durée du jour et de la nuit ne varie presque pas (même si la position du Soleil dans le ciel varie en longitude). Aux pôles, l'effet est extrême, si bien que le jour et la nuit y durent 6 mois chacun.
D'un point de vue astronomique, on peut noter quatre points particuliers sur la trajectoire d'une planète en fonction de son inclinaison :
- lorsque le côté nord de l'axe de la Terre penche vers le Soleil, c'est le solstice de juin, le jour le plus long pour l'hémisphère Nord. Le Soleil à midi est au zénith du tropique du Cancer, situé actuellement à une latitude d'environ 23° 26' 11" nord (valeur de obliquité moyenne au 1er janvier 2023). C'est le jour le plus court pour l'hémisphère Sud ;
- lorsque le côté sud de l'axe de la Terre penche vers le Soleil, c'est le solstice de décembre, le jour le plus court pour l'hémisphère Nord. Le Soleil à midi est au zénith du tropique du Capricorne, situés actuellement à une latitude d'environ 23° 26' 11" sud (valeur de obliquité moyenne au 1er janvier 2023). C'est le jour le plus long pour l'hémisphère Sud ;
- les deux autres points correspondent aux équinoxes de printemps et d'automne. L'axe se trouve alors dans un plan orthogonal à la direction du Soleil ; la durée des jours est égale à celle des nuits, au nord comme au sud, et le Soleil à midi est au zénith de l'équateur.
Complément
En ce qui concerne la Terre, une propriété importante de l'obliquité est la variation cyclique de sa valeur : celle-ci varie entre 24,5044° (ou 24° 30' 16") et 22,0425° (ou 22° 2' 33"), suivant un cycle d'environ 41 000 années. Les saisons varient donc suivant les millénaires de forte inclinaison ou d'inclinaison plus faible, une inclinaison plus forte impliquant des saisons plus marquées. Ce caractère cyclique est utilisé en cyclostratigraphie. Il a été démontré en 1993 par Jacques Laskar que la Lune stabilise la valeur de l'obliquité autour de 23° et l'empêche ainsi de varier de façon chaotique[6]. D'après W.R. Ward, le rayon de l'orbite de la Lune (lequel est en permanence en train de croître à cause des effets de marées) passera de 60 à 66,5 fois le rayon de la Terre en environ 1,5 milliard d'années[7]. Une résonance planétaire se produira alors, induisant des oscillations de l'inclinaison entre 22° et 38°. Ensuite, en approximativement 2 milliards d'années, quand la Lune atteindra la distance de 68 fois le rayon de la Terre, une autre résonance provoquera de plus grandes oscillations, entre 27° et 60°. Cela aura des effets extrêmes sur le climat, toutes considérations concernant l'activité solaire mises à part.
Inclinaison de l'axe dans le système solaire
| Type de corps | Corps | Inclinaison de l’axe | Commentaire |
|---|---|---|---|
| Planète | Mercure | 0,03° | |
| Vénus | 177,36° | La rotation de Vénus est rétrograde | |
| Terre | 23,44° | ||
| Mars | 25,19° | ||
| Jupiter | 3,12° | ||
| Saturne | 26,73° | ||
| Uranus | 97,8° | La rotation d'Uranus est rétrograde | |
| Neptune | 29,58° | ||
| Planète naine | Cérès | 4° | |
| Pluton | 122,53° | La rotation de Pluton est rétrograde | |
| Satellite naturel | Lune | 1,54° | Satellite naturel de la Terre |
| Callisto | 0,19° | Satellites naturels de Jupiter | |
| Europe | 0,47° | ||
| Io | 0,03° | ||
| Ganymède | 0,20° | ||
| Titan | 0,28° | Satellite naturel de Saturne | |
| Triton | 156,86° | Satellite naturel de Neptune. La rotation de Triton est rétrograde |
Voir aussi
- Pythéas
- Jacques d'Allonville de Louville
- Leonardo Ximenes
- Cycles de Milankovitch
Références
- ↑ (en) Obliquity of the Ecliptic, Nutation in Obliquity and Latitudes of the Arctic/Antarctic Circles
- ↑ Géographie : La rotation de la Terre
- ↑ Jean-Étienne Montucla, Histoire des mathématiques, volume 4, Henri Agasse, 1802, p. 226.
- ↑ Lelewel, Joachim (1836) : "Pythéas de Marseille et la géographie de son temps"
- ↑ Répertoire des constantes de l'Astronomie de J.C. Houzeau Directeur de l'observatoire Royal Annales de l'Observatoire de Bruxelles http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?bibcode=1878AnOBN...1....1H&db_key=AST&page_ind=16&plate_select=NO&data_type=GIF&type=SCREEN_GIF&classic=YES
- ↑ (en) J. Laskar, F. Joutel et P. Robutel, « Stabilization of the Earth's obliquity by the Moon », Nature, vol. 361, no 6413, , p. 615–617 (ISSN 0028-0836 et 1476-4687, DOI 10.1038/361615a0).
- ↑ Ward, W.R. (1982). "Comments on the Long-Term Stability of the Earth's Obliquity". Icarus 50: 444–448.
Liens externes
Phénomène des saisons expliqué par l'inclinaison de l'axe de la Terre