Intensité lumineuse

Données clés

Unités SI	candela (cd)
Dimension	J
Nature	Distribution angulaire extensive
Symbole usuel	${\displaystyle I}$ ou ${\displaystyle I_{v}}$
Lien à d'autres grandeurs	${\displaystyle \mathrm {d} I=L\ \mathrm {d} S\ \cos \theta }$

L’intensité lumineuse est une grandeur qui exprime la capacité d'une source ponctuelle de lumière à éclairer dans une direction donnée.

C'est une grandeur photométrique. Le rayonnement électromagnétique, qui constitue la lumière, n'est pas également perçu par la vision humaine ; l'expression de l'intensité lumineuse implique une pondération de la longueur d'onde par la fonction d'efficacité lumineuse spectrale, qui rend compte de la sensibilité visuelle humaine.

Dans le système international d'unités, l'intensité lumineuse se mesure en candelas (cd), une des unités de base ; elle se définit à partir de la luminance. L'intensité ne se mesure pas directement ; mais on a pu définir, de plusieurs manières au cours du temps, un étalon. Elle sert principalement pour le calcul de l'éclairement lumineux et pour préciser la répartition de la lumière qu'émet un luminaire ou une surface éclairée selon la direction.

Définition

Considérant la définition de la luminance et de l'étendue géométrique, l'intensité lumineuse ${\displaystyle I(\phi ,\theta )}$ s'exprime de la façon suivante^{[1],[2],[3],[4],[5]} :

${\displaystyle \mathrm {d} I=L(\phi ,\theta )\cos \theta \,\mathrm {d} \theta \,\mathrm {d} \phi \quad \Rightarrow \quad I=\int _{0}^{2\pi }\int _{0}^{\pi }L(\phi ,\theta )\cos \theta \,\mathrm {d} \phi \,\mathrm {d} \theta }$

où ${\displaystyle \mathrm {d} I}$ est l'intensité élémentaire correspondant à l'élément de surface ${\displaystyle \mathrm {d} S}$, ${\displaystyle \theta }$ est l'angle entre la direction portant ${\displaystyle L}$ et la normale à la surface source et ${\displaystyle \phi }$ l'angle de longitude compté par rapport à une origine arbitraire.

L'intensité lumineuse moyenne ${\displaystyle {\overline {I}}}$ dans l'intervalle fini d'angle solide ${\displaystyle \delta \Omega }$ s'exprime à partir du flux lumineux ${\displaystyle \delta \Phi }$ contenu dans cet angle par :

${\displaystyle {\overline {I}}={\frac {\delta \Phi }{\delta \Omega }}}$

On trouve cette expression abusivement écrite sous la forme ${\displaystyle I={\frac {\mathrm {d} \Phi }{\mathrm {d} \Omega }}}$, suggérant ainsi une dérivation. Or ${\displaystyle \Phi }$ est indépendant de ${\displaystyle \Omega }$ (c'est un flux) et donc ${\displaystyle {\frac {\mathrm {d} \Phi }{\mathrm {d} \Omega }}=0}$.

Perception humaine

La fonction d'efficacité lumineuse relative spectrale caractérise la sensibilité de l'œil de l'observateur de référence.

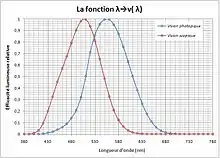
L'œil humain n'est sensible qu'à une petite partie du spectre électromagnétique (le domaine visible) et n'a pas la même sensibilité aux différentes longueurs d'onde auxquelles il est sensible. Dans un environnement lumineux (vision diurne, dite photopique), l'œil humain est le plus sensible au domaine de longueur d'onde correspondant à la perception du vert-jaune, vers 555 nanomètres. Ainsi, deux sources lumineuses de même puissance rayonnée en radiométrie et situées à égale distance d'un observateur n'ont pas forcément la même intensité lumineuse en photométrie. Une source monochromatique rayonnant dans le vert-jaune aura une intensité lumineuse perçue supérieure à une autre rayonnant dans le rouge ou dans le bleu.

Dans un environnement plus obscur, la vision humaine ne distingue plus les couleurs, et la sensibilité spectrale relative est décalée vers le bleu. On parle de vision scotopique. Entre les deux domaines de luminosité, on parle de vision mésopique.

Sauf précision contraire, l'intensité lumineuse concerne le domaine de la vision photopique.

Intensité et éclairement

On tire de la définition une relation entre l'intensité et l'éclairement lumineux d'un élément de surface ${\displaystyle \delta S}$, perpendiculaire à la direction du flux, à une distance d de la source. L'élément de surface intercepte un angle solide

${\displaystyle \delta \Omega ={\frac {\delta S}{d^{2}}}}$

donc

${\displaystyle {\overline {I}}={\frac {\delta \phi }{\delta \Omega }}=d^{2}{\frac {\delta \phi }{\delta S}}}$

Comme l'éclairement ${\displaystyle E}$ est égal au quotient du flux élémentaire par l'élément de surface, le flux est le produit ${\displaystyle E\;\delta S}$, et

${\displaystyle {\overline {I}}=E\,d^{2}}$

Si l'élément de surface n'est pas perpendiculaire au flux, celui-ci se répartit obliquement, et l'éclairement devient

${\displaystyle {\overline {I}}=E\,d^{2}\cos \theta }$

où ${\displaystyle \theta }$ est l'angle entre la normale à l'élément de surface et la direction du flux lumineux.

Une source à l'infini a un éclat apparent, mais ${\displaystyle \delta \Omega }$ est nul, les rayons lumineux étant parallèles. La luminance est alors définie au sens des distributions sous forme d'un produit de distributions de Dirac ${\displaystyle L=L_{0}\delta (\phi -\phi _{0})\delta (\theta -\theta _{0})}$ pour un faisceau d'orientation ${\displaystyle (\phi _{0},\theta _{0})}$. L'intensité lumineuse continue à être définie par :

${\displaystyle I=\int _{0}^{2\pi }\int _{0}^{\pi }L_{0}\delta (\phi -\phi _{0})\delta (\theta -\theta _{0})\cos \theta \,\mathrm {d} \phi \,\mathrm {d} \theta =L_{0}\cos \theta _{0}}$

C'est le cas en éclairage, avec la lumière du soleil ou de la lune ; on connaît alors l'éclairement lumineux des surfaces directement exposées, dans diverses conditions^[6]. En astronomie, on repère la magnitude apparente des étoiles à partir de l'éclairement énergétique, sans considération de la part du rayonnement visible.

Indicatrice d'émission

Indicatrice d'intensité d'une lampe.

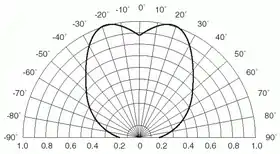
Les luminaires, les surfaces éclairées qui renvoient la lumière, et d'une façon générale les sources lumineuses n'éclairent pas avec la même intensité dans toutes les directions. L'indicatrice d'émission d'une source est proportionnelle à une surface dont la distance à la source est elle-même proportionnelle à l'intensité lumineuse dans la même direction^[7]. La longueur d'un point de cette courbe à l'origine représente la luminance. À la normalisation près, ce diagramme correspond à la notion de distribution angulaire.

Pour l'établir pour une source réelle, il faut assimiler celle-ci à une source ponctuelle ; on mesure l'éclairement moyen d'un élément de surface placé suffisamment loin de la source, et on calcule à partir de cette valeur celle de l'intensité de l'émission. Le diagramme représente souvent une intensité relative par rapport à celle relevée dans la direction principale^[3]. L'utilisation numérique requiert plutôt une normalisation dans un demi-espace, la norme étant définie par

${\displaystyle \int _{0}^{2\pi }\int _{0}^{\frac {\pi }{2}}L(\theta ,\phi )\cos \theta \mathrm {d} \theta \mathrm {d} \phi }$

Cas particuliers

Indicatrice d'intensité d'une source orthotrope.

Source lumineuse ponctuelle isotrope

Le flux lumineux issu d'une source lumineuse isotrope est uniformément réparti, son intensité lumineuse est la même dans toutes les directions. L'angle solide d'émission vaut ${\displaystyle {4\pi }}$ stéradians, ce qui conduit à la relation suivante entre le flux ${\displaystyle \Phi }$ et l'intensité lumineuse ${\displaystyle I}$ dans une direction quelconque^[8] : ${\displaystyle I={\frac {\Phi }{4\pi }}}$. L'enveloppe de son indicatrice est une sphère, représentée généralement par sa section circulaire.

Source lumineuse orthotrope

Une source lumineuse orthotrope présente une luminance identique dans toutes les directions. L'indicatrice est définie par : ${\displaystyle I(\theta )=I(0)\,\cos \theta }$. C'est le cas des sources diffusantes qui respectent la loi de Lambert.

Indicatrice parabolique

Certains systèmes d'éclairage à diode électroluminescente présentent une indicatrice de forme parabolique^[9].

Unités

Concentration du flux et intensité

La concentration d'un flux lumineux dans un pinceau fin augmente l'intensité lumineuse de la source dans la direction du pinceau.

Si toute la puissance d'un flux lumineux d'un lumen est concentrée et uniformément répartie dans un cône d'angle solide un stéradian, l'intensité lumineuse dans ce cône sera égale à la valeur moyenne, et sera par définition d'une candela. Si l'on change le dispositif optique pour concentrer ce faisceau dans un dixième de stéradian, l'intensité lumineuse dans le cône sera portée à dix candelas. À flux lumineux constant, l'intensité lumineuse est d'autant plus grande que le faisceau lumineux est étroit.

Annexes

Notes et références