Propriétés de la matière dégénérée

La matière est dite dégénérée lorsque sa densité et sa « faible » température font que les fermions (électrons principalement) occupent des niveaux d'énergie plus élevés que ce que la distribution de Maxwell prédit. Cela lui donne des propriétés particulières, à savoir :

• très faible compressibilité à masse constante ;
• pression et densité quasi indépendantes de la température ;
• conductivité thermique très élevée.

Les corps composés de matière dégénérée sont toujours très massifs (de l'ordre de 10³⁰ kg) et autogravitants, car un confinement considérable est nécessaire pour le maintien de cette matière. Par exemple, la matière composant une naine blanche a une densité de l'ordre d'un million de fois celle de l'eau, à une température de plusieurs centaines de milliers de degrés. Extraite de l'intense confinement et mise dans un environnement plus familier, cette matière exploserait et se diluerait très rapidement.

Équation d'état

Relation masse-rayon d'une naine blanche (courbe rouge). On observe effectivement que lorsque le rayon de l'étoile diminue, la masse tend vers une limite de 1,44 masse solaire. Les courbes verte et bleue représentent les cas d'un polytrope γ=5/3 et γ=4/3. Les points magenta, cyan et jaune représentent les coordonnées des étoiles Sirius B, Stein 2051 et 40 Eri B.

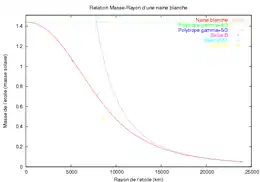
Les équations d'état sont assez faciles à calculer pour des gaz supposés fortement dégénérés et soit non-relativistes, soit ultrarelativistes. Pour un gaz fortement dégénéré non-relativiste, l'équation d'état s'écrit ${\displaystyle P\propto \rho ^{5/3}}$. Pour un corps massif, la résolution de l'équation hydrostatique donne un polytrope d'indice 3/2 dont le rayon est proportionnel à l'inverse du cube de la masse.

Pour un gaz ultrarelativiste (à proximité de la limite de Chandrasekhar), l'équation d'état devient ${\displaystyle P\propto \rho ^{4/3}}$, ce qui correspond à un polytrope d'indice 3. La résolution de l'équation hydrostatique pour un tel polytrope montre que la masse de l'objet considéré est forcément inférieure à une masse limite. C'est cette masse limite qui est appelée masse de Chandrasekhar. Pour un traitement relativiste complet, une interpolation entre les deux équations doit être faite. La figure ci-contre montre le rayon d'une naine blanche en fonction de sa masse.

Naine blanche

Une naine blanche, reste d'étoile après que les couches extérieures en ont été soufflées, est un astre formé de matière dégénérée, abritant une masse de l'ordre de celle du Soleil (1,9885  × 10³⁰ kg) dans une sphère d'un rayon de l'ordre de celui de la Terre, d'où une masse volumique très élevée. Pour une naine blanche composée de carbone et d'oxygène^[2], la masse de Chandrasekhar s'élève à 1,44 masse solaire (soit environ 2,863 × 10³⁰ kg). À l'issue de l'évolution d'une étoile, une naine blanche a une masse largement inférieure à la masse de Chandrasekhar (moins d'une masse solaire^[3]), mais peut accumuler de la matière, ce qui arrive notamment si une autre étoile orbite près d'elle. Sa masse augmentant, son rayon diminue jusqu'à ce que, près de la masse de Chandrasekhar, la contraction gravitationnelle et les épisodes de novae aient suffisamment réchauffé l'intérieur de l'étoile pour que se déclenche la fusion du carbone. Lorsque la réaction commence, l'augmentation de température à l'intérieur de l'astre est isochore à cause de la dégénérescence (indépendance de la température par rapport à la pression). Comme la réaction est très fortement dépendante de la température, elle s'emballe et l'énergie libérée dépasse l'énergie de liaison gravitationnelle de la naine blanche. Cette dernière devient une supernova de type Ia, à la différence des supernovas de type ll résultant de l'effondrement du cœur d'étoiles massives ayant consommé tous les éléments pouvant fusionner (jusqu'au fer) et générant une étoile à neutrons ou même un trou noir (au-dessus de 3,2 masse solaires résiduelles), les supernova de type la dispersent la totalité de leur masse. Ce sont de super bombes thermonucléaires faisant fusionner en un temps très court le carbone, l'azote et l'oxygène dont elles sont presque exclusivement constituées.

Cœur d'une étoile massive

Les étoiles d'une masse supérieure à 12 masses solaires sont assez chaudes pour que les réactions de fusion thermonucléaire conduisent à la formation de nickel 56 par fusion du silicium. Lorsque le silicium central a complètement été transformé en fer et en nickel 56^[4] il reste un noyau de nickel 56 et de fer inerte entouré par une couche de silicium toujours en réaction. Le noyau inerte se contracte jusqu'à atteindre la pression de dégénérescence des électrons, et constitue un corps dégénéré dont la masse de Chandrasekhar est d'environ 1,4 masse solaire. La fusion du silicium continue d'apporter du nickel, qui se dépose sur le corps et devient dégénéré à son tour. Lorsque la masse accumulée dépasse la masse de Chandrasekhar, l'effondrement gravitationnel se produit et la supernova commence, laissant une étoile à neutrons d'un diamètre de quelques dizaines de kilomètres et contenant au moins 1,5 fois la masse du soleil.

Bibliographie

• [Heyvaerts 2012] J. Heyvaerts, Astrophysique : étoiles, univers et relativité (cours et exercices corrigés), Paris, Dunod, août 2012, 2^e éd. (1^re éd. sept. 2006), 1 vol., X-384, ill., fig. et graph., 17 × 24 cm (ISBN 978-2-10-058269-3, EAN 9782100582693, OCLC 816556703, BNF 42740481, SUDOC 163817030, présentation en ligne, lire en ligne), chap. 5, sect. 5.3, § 5.3.1, Masse de Chandrasekhar, p. 89.
• [Taillet, Villain et Febvre 2018] R. Taillet, L. Villain et P. Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Sup., hors coll., sér. phys., janv. 2018, 4^e éd. (1^re éd. mai 2008), 1 vol., X-956, ill. et fig., 17 × 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, SUDOC 224228161, présentation en ligne, lire en ligne), s.v.masse de Chandrasekhar, p. 454, col. 2.

Articles connexes

• Limite d'Oppenheimer-Volkoff