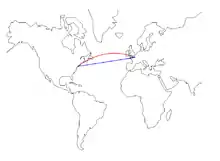


L'orthodromie désigne le chemin le plus court entre deux points d'une surface. Sur une sphère, c'est le plus petit des deux arcs du grand cercle joignant les deux points.
Pour les navigateurs, une route orthodromique désigne ainsi la route la plus courte à la surface du globe terrestre entre deux points. Elle est l'une des géodésiques de cette surface.
Dans la vie courante, cette plus courte distance entre deux points sur Terre est désignée sous le nom de « distance à vol d'oiseau » entre ces deux points[1].
Représentation sur une carte
Sur une carte en projection de Mercator, l'orthodromie n'est généralement pas représentée par une ligne droite mais par une ligne courbe. En effet, une carte en projection de Mercator conserve les angles mais pas les distances, de sorte que c'est la loxodromie (qui coupe tous les méridiens sous un angle constant) qui y sera représentée par une ligne droite.
Sur une carte en projection gnomonique, l'orthodromie est représentée par une droite. Les cartes en projection gnomonique sont utilisées pour la navigation en latitudes élevées.
La courbe de l'orthodromie sur la carte Mercator est ouverte vers l'équateur, soit courbée vers le pôle Nord dans l'hémisphère nord, sud dans l'hémisphère sud. Ceci signifie que pour une traversée est-ouest (et inversement) on va se rapprocher du pôle. Le point d'infléchissement de l'orthodromie s'appelle le sommet. La détermination de la latitude du sommet (latitude maximale atteinte) est une grandeur intéressante à déterminer pour préparer une traversée circumpolaire maritime — dans l'hémisphère sud par conséquent, par exemple de la Tasmanie au cap Horn — où il importe de ne pas trop gagner en latitude en raison du danger des glaces et de la banquise. La route choisie alors se décomposera en un tronçon d'orthodromie jusqu'à la latitude extrême que l'on ne veut pas dépasser, puis un tronçon de loxodromie à cette latitude et enfin un autre tronçon d'orthodromie pour remonter jusqu'à destination.
Formules relatives à l'orthodromie
Les formules ci-dessous sont données en assimilant la Terre à une sphère de 40 000 km de circonférence.
Distance orthodromique
Soit M la longueur de l'orthodromie exprimée en milles marins entre et , où désigne la latitude et la longitude. M est donnée par la formule suivante, la valeur de l'arc cosinus étant en degrés :
- .

En effet, en prenant le rayon de la sphère pour unité, les coordonnées cartésiennes des points A et B en coordonnées sphériques[2] exprimées en fonction de la latitude et de la longitude sont :
et
de sorte que le cosinus de l'arc AB, égal au produit scalaire des deux vecteurs OA et OB, vaut :
- .
Le coefficient 60 devant l'arc cosinus provient du fait que le mille marin (1 852 m) correspond à une minute d'arc sur un grand cercle de la surface terrestre, et donc 60 milles marins correspondent à un degré. Par conséquent, si on exprime arccos(AB) en degrés, on obtient la distance en milles marins en multipliant cet arc cosinus par 60.
Exemple : La distance orthodromique entre Paris (48° 51′ N, 2° 21′ E) et New York (40° 43′ N, 74° 00′ O) est d'environ 3 149 milles marins, soit 5 832 km, la Terre étant ici modélisée par une sphère de circonférence 40000 km.
On trouve également une expression de cette distance à l'aide de la fonction sinus verse (versin) ou de sa moitié (haversin):
Gain en distance par rapport à la loxodromie
Sur une courte distance, on peut confondre orthodromie et loxodromie. La distinction devient importante lors des voyages inter-continentaux, et surtout aux latitudes élevées.
À titre d'exemple, un voyage entre Paris et New York a une longueur loxodromique approximative de 6 070 km, et le parcours orthodromique permet de gagner 230 km. Le gain est de 1 600 km entre Paris et Tokyo, pour une longueur orthodromique de 9 700 km environ.
Route initiale (cap du tronçon de route initial)
Le parcours le long d'une orthodromie ne se faisant pas à cap constant, on découpe en général celle-ci en tronçons plus courts où l'on garde un cap constant, propre à chaque tronçon. Le cap du premier tronçon est l'angle Ro en degrés entre le Nord et la tangente en A à l'orthodromie, compté dans le sens des aiguilles d'une montre. Un cap de 0° correspond au Nord, 90° à l'Est, - 90° ou 270° à l'Ouest. L'angle Ro est donné par la formule suivante[3] :
- .
En effet, en prenant le rayon terrestre comme unité, le vecteur T tangent en A à l'orthodromie est égal à OB - (OB|OA)OA, où (OB|OA) désigne le produit scalaire des deux vecteurs. Ce vecteur appartient en effet au plan engendré par OA et OB, et est orthogonal à OA. Le vecteur unitaire u tangent en A au méridien et dirigé vers le Nord a pour composantes . Le vecteur unitaire v tangent en A au parallèle et dirigé vers l'Est a pour composantes . Ces deux vecteurs sont orthogonaux à OA. On a alors :
ce qui donne la formule annoncée.
Une autre formule possible est la suivante :
où sin(AB) est le sinus de l'arc AB. On trouve directement cette relation en appliquant la formule des sinus en trigonométrie sphérique au triangle ABN, où N est le pôle Nord. Dans ce triangle, l'angle en A est Ro et est opposé à l'arc , et l'angle au pôle est opposé à l'arc AB. On a donc :
- .
Exemple : Le premier cap à suivre pour aller de Paris (48° 51′ N, 2° 21′ E) à New York (40° 43′ N, 74° 00′ O) est de -68,21°, ou 291,79°, soit une direction ouest-nord-ouest, alors que New York se situe pourtant à une latitude inférieure à celle de Paris. L'orthodromie qui en est issue fait survoler la Cornouailles britannique et le Nord de la mer Celtique avant d'effleurer le Sud-Ouest de l'Irlande.
Coordonnées du vertex
Les vertex sont les deux points du grand cercle passant par A et B de latitude extrême (maximale ou minimale). Les deux vertex sont diamétralement opposés et l'orthodromie y coupe le méridien à angle droit. Ils ne se situent pas nécessairement sur la trajectoire entre A et B.
Latitude
Le cosinus de leur latitude est donné par :
- .
Pour le voir, on applique la formule des sinus en trigonométrie sphérique au triangle AVN, où V est le vertex et N le pôle Nord. Dans ce triangle, l'angle en V est droit, et opposé à l'arc . L'angle en A est Ro et est opposé à l'arc . On a donc :
- .
Exemple : Entre Paris (48° 51′ N, 2° 21′ E) et New York (40° 43′ N, 74° 00′ O), le vertex se situe à une latitude de 52,3°, supérieure à la latitude des deux villes.
Longitude
La différence de longitude entre le point de départ et le vertex est donnée par :
En effet, on applique la formule des cosinus en trigonométrie sphérique au triangle AVN, où V est le vertex et N le pôle Nord. Dans ce triangle, l'angle en V est droit, et opposé à l'arc . L'angle en A est Ro et est opposé à l'arc . L'angle en N est et opposé à l'arc AV. On a donc :
et donc :
On a également :
et donc :
On obtient la relation voulue en remplaçant dans par la valeur donnée dans la deuxième relation.
Exemple : Entre Paris (48° 51′ N, 2° 21′ E) et New York (40° 43′ N, 74° 00′ O), l'écart de longitude entre Paris et le vertex est de 28°.
Autres modèles de la Terre
La situation se complique considérablement si on prend pour la Terre un modèle autre que sphérique. D'une part, les définitions peuvent varier, mais la détermination explicite d'une orthodromie peut se révéler en général impossible à calculer.
On conserve généralement comme définition de l'orthodromie la courbe reliant deux points donnés et de longueur minimale[4], mais on trouve aussi comme définition celle d'une géodésique[5]. Or les deux notions peuvent se révéler différentes. Par exemple, dans le cas d'un ellipsoïde de révolution aplati, l'équateur est une géodésique mais pas une orthodromie, car si on prend deux points diamétralement opposés sur cet équateur, il est plus court de les joindre en passant par les pôles. Enfin, on peut aussi trouver comme définition de l'orthodromie la trace sur la surface terrestre du plan passant par le centre de la Terre et les deux points à relier, cette définition permettant une détermination plus facile de la courbe[6].
Notes et références
- ↑ « Pourquoi parle-t-on de distance "à vol d'oiseau" ? »
 , (consulté le )
, (consulté le ) - ↑ Les angles utilisés en coordonnées sphériques peuvent être différents. Il convient d'adapter les formules.
- ↑ Dans cette formule, on a pris la convention, usuelle en mathématiques, des longitudes croissantes vers l'Est. Si on prend comme convention que les longitudes croissent vers l'Ouest, il convient de changer le signe du second membre.
- ↑ « 1Guide de construction d’éléments géométriques, utilisation de GeodEasy et ACADEMIC », (consulté le ), p. 7
- ↑ « Géométrie de l'ellipsoïde » (consulté le ), p. 33
- ↑ Henri de Sarrauton, « Exposé du système de l'heure décimale », Bulletin de la Société de géographie, 7e série, t. 19, , p. 99 (lire en ligne)
Voir aussi
Articles connexes
- Arc de méridien
Liens externes
- « Orthodromie », sur École nationale de la Marine marchande de Marseille




![M = 60\arccos \,[\sin(\varphi_A)\sin(\varphi_B) + \cos(\varphi_A)\cos(\varphi_B) \cos (\lambda_B - \lambda_A)]\,](https://img.franco.wiki/i/cad7fd54d4b55a5e9c8d2e5a9cbb7dc7e2bde8b8.svg)























