La structure cristalline (ou structure d'un cristal) donne l'arrangement des atomes dans un cristal. Ces atomes se répètent périodiquement dans l'espace sous l'action des opérations de symétrie du groupe d'espace et forment ainsi la structure cristalline. Cette structure est un concept fondamental pour de nombreux domaines de la science et de la technologie. Elle est complètement décrite par les paramètres de maille du cristal, son réseau de Bravais, son groupe d'espace et la position des atomes dans l'unité asymétrique la maille. Pour cette raison, ce sont les données que l'on retrouve dans tous les fichiers d'échange d'informations cristallographiques, comme les fichiers CIF.

Réseau cristallin

Un solide cristallin est constitué par la répétition périodique dans les 3 dimensions de l'espace d'un motif atomique ou moléculaire, contenu dans une unité de répétition périodique appelé maille ; de la même façon qu'un papier peint est constitué de la répétition d'un même motif. La périodicité de la structure d'un cristal est donc représentée par un ensemble de points régulièrement disposés. Cet ensemble est appelé réseau cristallin et les points le constituant sont appelés nœuds du réseau.

À cause de la périodicité du réseau, toute paire de nœuds (O, M) définit un vecteur :

${\displaystyle {\overrightarrow {\mathrm {OM} }}=m_{1}\,{\vec {a_{1}}}+m_{2}\,{\vec {a_{2}}}+m_{3}\,{\vec {a_{3}}}}$

${\displaystyle m_{1}}$, ${\displaystyle m_{2}}$, ${\displaystyle m_{3}}$ étant des entiers relatifs si la maille choisie pour décrire le réseau est primitive.

Les trois vecteurs ${\displaystyle {\vec {a_{1}}}}$, ${\displaystyle {\vec {a_{2}}}}$ et ${\displaystyle {\vec {a_{3}}}}$ sont linéairement indépendants et constituent une base du réseau cristallin. Pour chaque réseau, il existe une infinité de bases.

Le réseau cristallin est aussi appelé réseau direct, par opposition au réseau réciproque, qui est sa transformée de Fourier et que l'on observe par des expériences de diffractométrie.

Maille élémentaire, maille conventionnelle

Une maille élémentaire (ou primitive) est une maille de volume minimal qui contient un seul nœud du réseau. La répétition périodique de cette maille dans les trois dimensions de l'espace suffit à reproduire l'intégralité du réseau et de la structure. Souvent, pour des raisons de commodité ou pour faire mieux ressortir la symétrie, on utilise pour décrire le cristal une maille multiple, contenant plusieurs nœuds et qui n'est donc pas élémentaire : c'est la maille conventionnelle. La multiplicité de la maille est alors définie par le nombre de nœuds qu'elle contient.

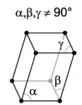
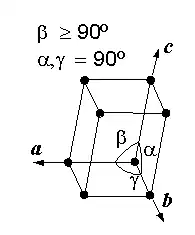
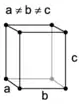
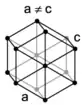
Une maille est définie par les trois vecteurs de base a, b et c. Le choix de ces trois vecteurs n'est pas unique, on peut donc définir plusieurs mailles élémentaires qui pourront plus ou moins bien montrer la symétrie du réseau. On utilise généralement les paramètres de maille : les longueurs des vecteurs, ${\displaystyle a}$, ${\displaystyle b}$ et ${\displaystyle c}$, et les angles formés entre eux, α, β et γ. Deux mailles de même multiplicité mais définies par des vecteurs de base différents occupent le même volume. Pour un réseau cristallin donné, une maille de multiplicité m occupe le volume mV, V étant le volume de la maille élémentaire du réseau.

Réseau de Bravais

Un réseau de Bravais est un réseau de nœuds obtenu par translation suivant des vecteurs de base à partir d'un nœud unique. Les réseaux de Bravais sont classés en 14 types en trois dimensions (5 types en deux dimensions) et représentent la périodicité de la structure cristalline. Celle-ci est obtenue à partir d'un ensemble minimal d'atomes occupant l'unité asymétrique, répétés dans l'espace selon les opérations du groupe d'espace du cristal. Tous les matériaux cristallins ont une périodicité correspondant à l'un de ces réseaux (mais pas les quasi-cristaux). Les 14 types de réseau de Bravais en trois dimensions sont listés dans le tableau ci-dessous.

Système réticulaire	triclinique ou anortique	monoclinique	orthorhombique	hexagonal	rhomboédrique	tétragonal (ou quadratique[1])	cubique (ou isométrique)
Réseau primitif ou simple	aP	mP	oP	hP	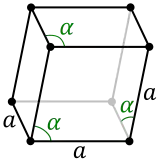hR	tP	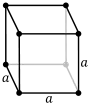cP
Réseau centré			oI			tI	cI
Réseau à base centrée		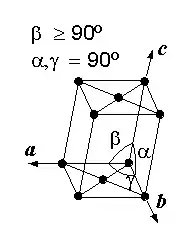mS	oS
Réseau à faces centrées		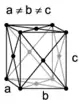	oF		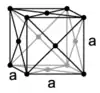		cF

Groupe d'espace, unité asymétrique

Le groupe d'espace d'un cristal contient l'ensemble des opérations de symétrie de la structure cristalline. On ne considère ici pas seulement la maille mais aussi les atomes qu'elle contient.

L'unité asymétrique d'un cristal est le plus petit volume à l'intérieur de la maille à partir duquel l'ensemble du cristal infini peut être reconstitué en appliquant les opérations de symétrie du groupe d'espace. Dans le cas du groupe d'espace triclinique P1, l'unité asymétrique est la totalité de la maille ; dans les autres groupes d'espace, elle est plus petite que la maille. Le volume de la maille est un multiple entier du volume de l'unité asymétrique.

Le groupe ponctuel de symétrie de l'unité asymétrique est 1 lorsque l'on considère les atomes qu'elle contient : il ne contient pas d'autres opérations de symétrie que l'identité, d'où le nom « asymétrique ». Cependant, la forme du volume défini par l'unité asymétrique peut avoir une symétrie supérieure.

Position des atomes

Pour décrire la structure d'un cristal, connaissant sa maille conventionnelle, ses paramètres de maille et son groupe d'espace (et donc son réseau de Bravais), il suffit de connaître la position des atomes dans l'unité asymétrique. Les atomes contenus dans l'unité asymétrique sont tous indépendants par symétrie les uns des autres : leurs positions appartiennent toutes à des orbites cristallographiques différentes.

Les positions des atomes sont données par leurs coordonnées ${\displaystyle x}$, ${\displaystyle y}$ et ${\displaystyle z}$ dans la base formée par les vecteurs de la maille a, b et c.

Polyèdres de coordination

À partir de toutes ces informations, il est possible de décrire plus précisément une structure cristalline, en déterminant les polyèdres de coordination formés par les atomes et la façon dont ces polyèdres sont reliés entre eux. Cela permet de comparer plus facilement différentes structures cristallines.

Structures types

Il existe beaucoup de cristaux isostructurels entre eux, c'est-à-dire qu'ils forment la même structure, bien que leurs compositions chimiques, donc la taille des ions, donc le paramètre de maille, peuvent être différents : les atomes et surtout les polyèdres de coordination sont arrangés de façon très similaire. Ils cristallisent alors dans une « structure type », qui est utilisée pour désigner la structure de tous ces cristaux.

Par exemple, la structure de la pérovskite CaTiO₃ est retrouvée, souvent déformée par rotation des octaèdres BX₆, dans plusieurs matériaux de formule générale ABX₃, comme BaTiO₃, PbZrO₃, etc. On dit qu'ils cristallisent dans la structure pérovskite.

Notes et références

Voir aussi