Dans la théorie des ensembles, l'union ou réunion^[1] est une opération ensembliste de base. En algèbre booléenne, l'union est associée à l'opérateur logique « ou inclusif » et est notée ∪.

L'union des ensembles A et B est représentée dans ce diagramme de Venn par l'ensemble de la zone colorée en bleu.

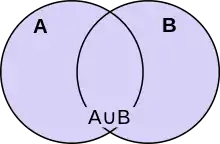
Union de deux ensembles

L'union de deux ensembles A et B est l'ensemble qui contient tous les éléments qui appartiennent à A ou appartiennent à B. On la note A ∪ B et on la dit « A union B »

Formellement :

${\displaystyle x\in A\cup B\Leftrightarrow \left(x\in A\lor x\in B\right)}$.

Par exemple l'union des ensembles A = {1, 2, 3} et B = {2, 3, 4} est l'ensemble {1, 2, 3, 4}.

Propriétés algébriques

• L'union est associative, c'est-à-dire que, pour des ensembles A, B et C quelconques, on a :
  (A ∪ B) ∪ C = A ∪ (B ∪ C).
• L'union est commutative, c'est-à-dire que, pour des ensembles A et B quelconques, on a :
  A ∪ B = B ∪ A.
• L'intersection est distributive sur l'union, c'est-à-dire que, pour des ensembles A, B et C quelconques, on a :
  A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
• L'union est distributive sur l'intersection, c'est-à-dire que, pour des ensembles A, B et C quelconques, on a :
  A ∪ (B ∩ C) = (A ∪B) ∩(A ∪ C).

Union d'une famille d'ensembles

On généralise ce concept à un ensemble quelconque ${\displaystyle X}$ d'ensembles (non nécessairement réduit à une paire, ni même fini) : sa réunion, notée ${\displaystyle \bigcup X}$, a pour éléments tous les ${\displaystyle x}$ pour lesquels il existe un ${\displaystyle E\in X}$ tel que ${\displaystyle x\in E}$ (si X est l'ensemble vide, cette réunion est donc vide^[2]). L'axiome de la réunion est l'affirmation que ${\displaystyle \bigcup X}$ est un ensemble^[3].

On peut alors définir la réunion d'une famille quelconque d'ensembles ${\displaystyle (E_{i})_{i\in I}}$ : c'est la réunion de l'ensemble ${\displaystyle X=\{E_{i}|i\in I\}}$. Cette réunion notée ${\displaystyle \bigcup _{i\in I}E_{i}}$ est donc l'ensemble des éléments ${\displaystyle x}$ pour lesquels il existe un ${\displaystyle i\in I}$ tel que ${\displaystyle x\in E_{i}}$. Formellement :

${\displaystyle x\in \bigcup _{i\in I}E_{i}\Leftrightarrow (\exists i\in I,\ x\in E_{i})}$.

La distributivité de l'intersection ci-dessus s'étend aux familles :

${\displaystyle A\cap \left(\bigcup _{i\in I}E_{i}\right)=\bigcup _{i\in I}(A\cap E_{i})}$.

Notes et références

Articles connexes

• Union disjointe
• Algèbre des parties d'un ensemble
• Diagramme de Venn
• L'axiome de la réunion en théorie des ensembles