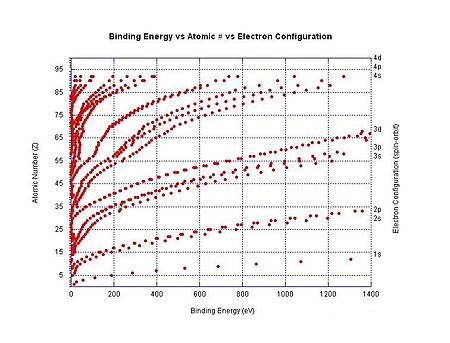
طاقة التأين لذرة هي الطاقة اللازمة لنزع إلكترون منها.[1][2][3] وطاقة التأين ذات أهمية كبيرة في الكيمياء الفيزيائية نظرا لأنها مقياس لقوة ترابط إلكترون بالذرة. إذا كان الترابط بين الإلكترون ونواة الذرة كبيرا زادت الطاقة التي يجب أن نمد بها الإلكترون لمغادرة الذرة والانفصال عنها.
ويمكننا القول أن طاقة التأين هي مقدار الطاقة اللازمة لفصل الإلكترون الأقل ارتباطًا بنواة الذرة في الحالة الغازية، وهو إلكترون التكافؤ، وإن قيمة هذه الطاقة تدلنا على صعوبة نزع الإلكترون من الذرة، فكلما كانت كبيرة كان تأين العنصر صعبًا. وفي أغلب الأحيان يحدث النزع على عدة خطوات متتالية وتسمى الطاقة لنزع الإلكترون الأول "طاقة التأين الأولى"، وعندما ننتزع إلكترونا ثانيا من الذرة فيلزم لذلك "طاقة التأين الثانية"، وهكذا بالنسبة إلى الإلكترونات التالية لها.
وغالبًا ما تحدث هذه العملية بتسليط أشعة ضوئية ذات تردد معين على العنصر في حالته الغازية فيمتصها الإلكترون ويـُنتزع من الذرة. وتختلف ترددات الضوء اللازمة لانتزاع إلكترون من ذرة العنصر باختلاف العنصر. فطاقة التأين تعتمد أولا على نوع العنصر، كما تعتمد على، هل هو الإلكترون الأول أم الإلكترون الثاني أم الثالث. ومن الطبيعي أنه كلما كان حجم العنصر صغيرًا كانت جاذبية النواة للإلكترون الخارجي قوية ويصعب بذلك نزعه. ولهذا السبب نجد أن طاقة التأين تزداد للعناصر من اليسار إلى اليمين في الدورة الواحدة في الجدول الدوري وتتناقص من أعلى إلى أسفل في المجموعة.
القيم والإتجاهات
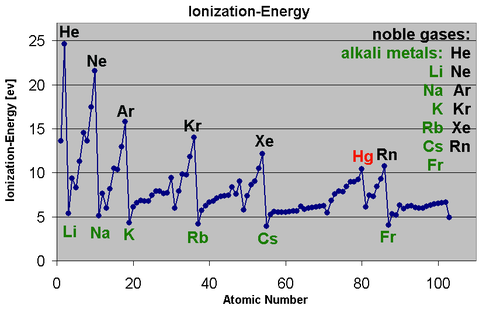
بصفة عامة، فإن طاقة التأين تقل خلال المجموعة بالجدول الدوري من الأعلى إلى الأسفل، ومن جهة أخرى، فإنها تزيد من اليسار إلى اليمين خلال الدورة وذلك بسبب زيادة العدد الذري الذي معناه زيادة الشحنة النووية الفعالة (الشحنة النووية الفعالة = شحنة النواة - معامل الحجب). وزيادة عدد البروتونات في النواة يؤدي إلى زيادة جذب الإلكترونات في الذرة ومن ضمنها المستويات الخارجية. لذلك فتزداد الطاقة اللازمة لنزع إلكترون من الذرة، أي تزداد طاقة التأين. كما أن طاقة التأين تتناسب عكسيا مع نصف القطر الذري فكلما ازداد نصف القطر الذري زاد بُعد إلكترونات المستويات الخارجية عن النواة وقل جذب النواة لها، فيسهل نزعها من الذرة، أي تقل طاقة التأين.
وعندما نقوم بنزع الإلكترون الخارجي الأول من الذرة، ونبدأ في نزع الإلكترون الذي يليه من مداره الذري نجد زيادة كبيرة في طاقة التأين. هذا لأنه بعد انتزاع الإلكترون الأول وانتقالنا لنزع الإلكترون الثاني يكون هذا أقرب للنواة، فتزداد الطاقة اللازمة لانتزاعه. تكون الإلكترونات الموجودة في مدارات قريبة من النواة مرتبطة بها بقوى جذب كهرستاتيكية أكبر، وعلى هذا تتطلب طاقة أكبر لانتزاعها.
بعض قيم طاقة التأين للدورة الثالثة في الجدول التالي:
| العنصر | الأولى | الثانية | الثالثة | الرابعة | الخامسة | السادسة | السابعة |
|---|---|---|---|---|---|---|---|
| Na | 496 | 4560 | |||||
| Mg | 738 | 1450 | 7730 | ||||
| Al | 577 | 1816 | 2744 | 11600 | |||
| Si | 786 | 1577 | 3228 | 4354 | 16100 | ||
| P | 1060 | 1890 | 2905 | 4950 | 6270 | 21200 | |
| S | 999 | 2260 | 3375 | 4565 | 6950 | 8490 | 11000 |
| Cl | 1256 | 2295 | 3,850 | 5,160 | 6,560 | 9,360 | 11,000 |
| Ar | 1,520 | 2,665 | 3,945 | 5,770 | 7,230 | 8,780 | 12,000 |
نلاحظ قفزات كبيرة في طاقة التأين المولية عند تعدية بنية غاز خامل. وعلى سبيل المثال نرى أن الطاقتين الأولتين لتأين 1 مول من المغنسيوم (نزع إلكترونين من المدار 3s ) تكونان أقل بكثير من الطاقة اللآزمة لانتزاع إلكترون ثالث (من المدار 2p ) الذي له ينية النيون في بنية Mg2+.
التفسير الكهرستاتيكي
يمكن توقع طاقات التأين باستخدام تحليل بسيط عن طريق الجهد الكهرستاتيكي ونموذج بور للذرة كالآتي:
بافتراض إلكترون له الشحنة e-، و أيون له شحنة ne+، حيث n هي عدد الإلكترونات المفقودة من الذرة. وطبقا لنموذج بور، يقترب الإلكترون من مالانهاية من الذرة ويرتبط. يتخذ مدارا حول النواة وهو على بُعد نصف قطر بور a. فيكون الجهد الكهرستاتيكي على مسافة a:
وحيث أن الإلكترون له شحنة سالبة، ومنجذب إلى الجهد الموجب للنواة (وقيمة هذا الجهد يسمى جهد التأين) فتلزمه طاقة ليقفز ويترك الذرة قدرها:
وهذا التحليل البسيط غير كامل ويترك المسافة a غير معروفة. ويمكن أن يكون أكثر دقة بتحديد هذه المسافة لكل إلكترون في العناصر الكيميائية، وعلى هذا تتطابق العلاقة مع التجارب العملية.
التفسير طبقا لميكانيكا الكم
طبقا لنظرية ميكانيكا الكم يتم وصف الإلكترون كسحابه للأماكن المتوقع وجوده فيها (في مدار إلكتروني) وهي تعطي لتواجد الإلكترون احتمالات تتراوح بين القرب والبعد r عن النواة. ويمكن بميكانيكا الكم حساب الطاقة بتكامل هذه السحابة، وتكون أبسط صيغة لطاقة تأين كالتالي:
حيث H ال هاملتوني (ميكانيكا الكم)، و هي الدالة الموجية للحالة القاعية للإلكترون. وطبقا لمعادلة هاميلتون تكون H مكونة من طاقة الحركة و طاقة الوضع للإلكترون حيث يوجد بالقرب من النواة الموجبة الشحنة ويقع تحت تأثير جهدها الكولومي:
حيث أن Z هي الشحنة النووية و مؤثر التدرج الذي يصف حركة الإلكترون. وأمكن العلماء حل المعادلة في حالة ذرة الهيدروجين حيث شحنة النواة تكون +1. وحصلوا على طاقة المدار وبُعد المدار عن النواة في نموذج بور، وعرّفوه بالمسافة المحددة حيث هي نصف قطر بور.
وبصفة عامة، فإن حساب طاقة التأين n لذرة فيها عدد Z من الإلكترونات (وبالتالي بروتونات) يزداد صعوبة حيث أن الإلكترونات التحتية الموجودة في الغلاف الإلكتروني تتفاعل مع النواة ومع الإلكترونات الخارجية وتزيد المسألة صعوبة. ولكنها موضوع جيد للدراسة، ويتم بصفة منتظمة في الكيمياء الحسابية.
موضوعات متعلقة
- جهد التأين مساوي لطاقة التأين مقسومة على شحنة الإلكترون.
- معادلة الشغل هي الطاقة اللازمة لنزع إلكترون من المادة الصلبة.
- أيون.
- نظرية كوبمان
مراجع
- "ionization potential". IUPAC gold book. مؤرشف من الأصل في 04 مارس 2016.
- "Ionization Energy". ChemWiki. UC Davis. مؤرشف من الأصل في 31 مارس 2014.
- "The difference between a vertical ionization energy and adiabatic ionization energy". Computational Chemistry Comparison and Benchmark Database. المعهد الوطني للمعايير والتقنية. مؤرشف من الأصل في 22 ديسمبر 2017.







