معادلات حركة المكبس

المكبس (أعلى) وذراع التوصيل في مكبس آلة .

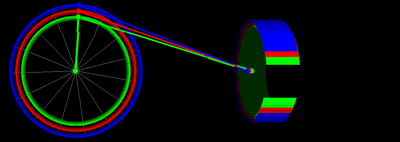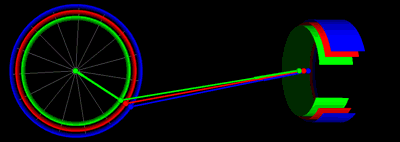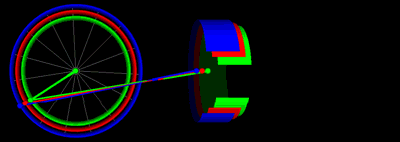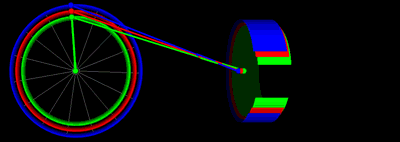
يمكن التعبير عن حركة المكابس الموصلة بعمود المرفق من خلال ذراع التوصيل كما يوجد في محركات الاحتراق الداخلي من خلال بعض المعادلات الرياضية ونناقش في هذه المقالة كيف تم استنتاج تلك المعادلات ومثال تصويري لها.

هندسة عمود المرفق

رسم توضيحي يُظهر تخطيطًا هندسيًا لوصلة المكبس وعمود المرفق ومركز عمود المرفق

التعريفات

l = طول ذراع التوصيل ( المسافة بين وصلة المكبس ووصلة عمود المرفق)
r = نصف قطر عمود المرفق (المسافة بين وصلة عمود المرفق ومركز عمودالمرفق أو نصف الشوط)
A = زاوية عمودالمرفق ( مُقاسة من مركز قطر الاسطوانة عند النقطة الميتة العليا
x = موضع وصلة المكبس (أعلي مركز عمود المرفق علي طول مركز قطر الاسطوانة)
v =سرعة المكبس.
a =تسارع المكبس داخل الاسطوانة.
ω =السرعة الزاوية لعمود المرفق مُقاسة بوحدة راديان لكل ثانية (rad/sec).

السرعة الزاوية

السرعة الزاوية لعمود المرفق مرتبطة بعدد دورات المحرك لكل دقيقة وتُحسب من العلاقة الآتية

${\displaystyle \omega ={\frac {2\pi \cdot \mathrm {RPM} }{60}}}$

العلاقة المثلثية

كما هو موضح في الشكل التوضيحي فإن وضع كل من وصلة عمود المرفق ومركز عمود المرفق ووصلة المكبس يشكلوا مثلثًا، وباستخدام قانون جيب التمام يتضح أن

${\displaystyle l^{2}=r^{2}+x^{2}-2\cdot r\cdot x\cdot \cos A}$

المعادلات بالنسبة للوضع الزاوي (المجال الزاوية)

المعادلات التالية توضح الحركة الترددية لمكبس بالنسبة لزاوية عمود المرفق، وموضح أيضًا ببعض الصور التوضيحية أمثلة لبعض من تلك المعادلات.

وضع المكبس

يمكن استنتاج معادلة توضح وضع المكبس بالنسبة لزاوية عمود المرفق كالتالي

${\displaystyle l^{2}-r^{2}=x^{2}-2\cdot r\cdot x\cdot \cos A}$

${\displaystyle l^{2}-r^{2}=x^{2}-2\cdot r\cdot x\cdot \cos A+r^{2}[(\cos ^{2}A+\sin ^{2}A)-1]}$

${\displaystyle l^{2}-r^{2}+r^{2}-r^{2}\sin ^{2}A=x^{2}-2\cdot r\cdot x\cdot \cos A+r^{2}\cos ^{2}A}$

${\displaystyle l^{2}-r^{2}\sin ^{2}A=(x-r\cdot \cos A)^{2}}$

${\displaystyle x-r\cdot \cos A={\sqrt {l^{2}-r^{2}\sin ^{2}A}}}$

وبالتالي تكون المعادلة هي

${\displaystyle x=r\cos A+{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}$

سرعة المكبس

يمكن التعبير عن سرعة المكبس بالنسبة لزاوية عمود المرفق من المعادلات التالية (باستخدام المشتقة الأولي لمعادلة موضع المكبس السابقة وتطبيق قاعدة السلسلة)

${\displaystyle {\begin{array}{lcl}x'&=&{\frac {dx}{dA}}\\&=&-r\sin A+{\frac {({\frac {1}{2}}).(-2).r^{2}\sin A\cos A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}\\&=&-r\sin A-{\frac {r^{2}\sin A\cos A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}\end{array}}}$

التسارع (العجلة)

يمكن استنتاج معادلة لتسارع مكبس المحرك بالنسبة لزاوية عمود المرفق ( باستخدام المشتقة الثانية لمعادلة موضع المكبس السابقة وتطبيق قاعدة السلسلة)

${\displaystyle {\begin{array}{lcl}x''&=&{\frac {d^{2}x}{dA^{2}}}\\&=&-r\cos A-{\frac {r^{2}\cos ^{2}A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {-r^{2}\sin ^{2}A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {r^{2}\sin A\cos A.(-{\frac {1}{2}})\cdot (-2).r^{2}\sin A\cos A}{\left({\sqrt {l^{2}-r^{2}\sin ^{2}A}}\right)^{3}}}\\&=&-r\cos A-{\frac {r^{2}(\cos ^{2}A-\sin ^{2}A)}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {r^{4}\sin ^{2}A\cos ^{2}A}{\left({\sqrt {l^{2}-r^{2}\sin ^{2}A}}\right)^{3}}}\end{array}}}$

المعادلات بالنسبة إلى الزمن (المجال الزمني)

مشتقات السرعة الزاوية

إذا كانت السرعة الزاوية ثابتة فإن

${\displaystyle A=\omega t\,}$

ويمكن حينئذ تطبيق العلاقات التالية:

${\displaystyle {\frac {dA}{dt}}=\omega }$

${\displaystyle {\frac {d^{2}A}{dt^{2}}}=0}$

التحويل من المجال الزاوي إلي المجال الزمني

المعادلات التالية توضح الحركة الترددية للمكبس بالنسبة إلي الزمن.

إذا كان مطلوبًا التعامل مع المجال الزمني بدلًا من المجال الزاوي فإن أولًا يتم استبدال A بωt في المعادلات السابقة ومن ثم يتم عمل مقياس للسرعة الزاوية كالتالي:

موضع المكبس

موضع المكبس بالنسبة للزمن ببساطة:

${\displaystyle x\,}$

سرعة المكبس

سرعة المكبس بالنسبة للزمن (بتطبيق [[قاعدة السلسلة):

${\displaystyle {\begin{array}{lcl}v&=&{\frac {dx}{dt}}\\&=&{\frac {dx}{dA}}\cdot {\frac {dA}{dt}}\\&=&{\frac {dx}{dA}}\cdot \ \omega \\&=&x'\cdot \omega \\\end{array}}}$

تسارع المكبس

تسارع حركة المكبس بالنسبة للزمن يمكننا الحصول علي معادلة لها كالآتي (بتطبيق قاعدة السلسلة و قاعدة الضرب وباستخدام مشتقات السرعة الزاوية):

${\displaystyle {\begin{array}{lcl}a&=&{\frac {d^{2}x}{dt^{2}}}\\&=&{\frac {d}{dt}}{\frac {dx}{dt}}\\&=&{\frac {d}{dt}}({\frac {dx}{dA}}\cdot {\frac {dA}{dt}})\\&=&{\frac {d}{dt}}({\frac {dx}{dA}})\cdot {\frac {dA}{dt}}+{\frac {dx}{dA}}\cdot {\frac {d}{dt}}({\frac {dA}{dt}})\\&=&{\frac {d}{dA}}({\frac {dx}{dA}})\cdot ({\frac {dA}{dt}})^{2}+{\frac {dx}{dA}}\cdot {\frac {d^{2}A}{dt^{2}}}\\&=&{\frac {d^{2}x}{dA^{2}}}\cdot ({\frac {dA}{dt}})^{2}+{\frac {dx}{dA}}\cdot {\frac {d^{2}A}{dt^{2}}}\\&=&{\frac {d^{2}x}{dA^{2}}}\cdot \omega ^{2}+{\frac {dx}{dA}}\cdot 0\\&=&x''\cdot \omega ^{2}\\\end{array}}}$

مقياس للسرعة الزاوية

كما لاحظنا أن x بدون مقياس، أما x' تم قياسها بالنسبة ل ω و x" تم قياسها بالنسبة لω².
لتحويل من سرعة بالنسبة للزاوية (إنش/راديان) إلي سرعة بالنسبة للزمن (إنش/ثانية) يتم ضرب x' في ω (راديان/ثانية).
ولتحويل x" من التسارع بالنسبة للزاوية (إنش/راديان²) إلي تسارع بالنسبة إلي الزمن (بوصة/ثانية²) يتم ضرب x" في ω² [rad²/s²].

• ونلاحظ أنه باستخدام بالتحليل البعدي فنجد أن الوحدات متسقة.

السرعة القصوى والصغرى

التسارع بدون عبور

السرعة العظمى والصغرى لا تحدث عندما تكون قيم زاوية عمود المرفق (A) أكبر من أو أقل من 90°.

والسرعة العظمي والصغري تحدث عند الزواية التي تعتمد علي طول ذراع التوصيل (l) ونص طول الشوط (r)، وتطابق زوايا عمود المرفق عندما يكون التسارع يساوي صفرًا (المرور بالمحور الأفقي).

زاوية عمود المرفق وذراع التوصيل ليست قائمة

السرعة العظمي والصغري لا تحدث بالضرورة عندما يكون عمود المرفق في وضع عمودي مع ذراع التوصيل (بينهما زاوية قائمة)، و هناك أمثلة مضادة تضحد تلك الفكرة بأن السرعة القصوي والصغري ربما تحدث عندما تكون الزاوية قائمة بين ذراع التوصيل وعمود المرفق.

مثال

عندما يكون عندنا ذراع توصيل بطول 6 إنش ونصف قطر عمود المرفق 2 إنش فإنه بحل معادلة التسارع رياضيًا عند وضع عدم الاجتياز نجد أن السرعة القصوي والصغري تحدث عند زاوية عمود المرفق ±73.17615°.

من ثم، باستخدام قانون الجيب المثلثي نجد أن عمود المرفق وذراع التوصيل يصنعان زاوية تُقدر ب88.21738° وأن الزاية الرأسية لذراع التوصيل هي 18.60647°.
ومن الواضح من هذ المثال أن الزاوية غير قائمة بين عمود المرفق وذراع التوصيل.

(للتأكد من زوايا المثلث عندئذ 88.21738° + 18.60647° + 73.17615° = 180.00000°)

ومثال واحد مضاد يكفي لضحد مقولة أن السرعة القصوي والصغري لا تحدثان إلا عند الزاوية القائمة بين عمود المرفق وذراع التوصيل.

رسم بياني لحركة المكبس

الرسم البياني التالي يوضح x, x', x" بالنسبة لزاوية عمود المرفق وبأطوال أشواط مختلفة حيث L = طول ذراع التوصيل (l) و R = نصف طول الشوط (r):

وحدات المحور الرأسي البوصة للموضع و (بوصة/راديان) للسرعة و (بوصة/راديان²) للتسارع.
وحدات المحور الأفقي هي الدرجة لزاوية عمود المرفق

رسم متحرك يوضح حركة المكابس بنفس قيم طول ذراع التوصيل ونصف قطر عمود المرفق في الرسم السابق:

رسم متحرك لحركة المكابس بقيم مختلفة لأطوال الشوط

مقالات ذات صلة

• محرك متردد
• محرك احتراق داخلي

موسوعات ذات صلة :

• موسوعة هندسة ميكانيكية