في الميكانيكا السماوية، معامل الجاذبية القياسي μ للأجرام الفلكية هو حاصل ضرب ثابت الجاذبية G في كتلة الجرم M.
| الجسم | μ (m3 s−2) |
|---|---|
| الشمس | 1.32712440018(9)×1020[1] |
| عطارد | 2.2032(9)×1013 |
| الزهرة | 3.24859(9)×1014 |
| الأرض | 3.986004418(9)×1014 |
| القمر | 4.9048695(9)×1012 |
| المريخ | 4.282837(2)×1013[2] |
| سيريس | 6.26325×1010[3][4][5] |
| المشتري | 1.26686534(9)×1017 |
| زحل | 3.7931187(9)×1016 |
| أورانوس | 5.793939(9)×1015[6] |
| نبتون | 6.836529(9)×1015 |
| بلوتو | 8.71(9)×1011[7] |
| إريس | 1.108(9)×1012[8] |
في نظام الوحدات الدولي معامل الجاذبية القياسي هو م3 ث−2.ومع ذلك، وحدات كم3 ث−2 كثيرا ما تستخدم في المطبوعات العلمية وفي ملاحة المركبات الفضائية.وقيمة معامل الجاذبية القياسي لعدة أجرام في النظام الشمسي معروفة بدقتها الأكبر من القيم الفردية لثابت الجاذبية وكتلة الجرم.[9]
دوران جسم صغير حول جسم رئيسي
يمكن تعريف الجسم الرئيسي (المركزي) في النظام المداري بأنه الجهاز الذي تكون كتلته (M) أكبر بكثير من كتلة الجسم المداري (m)،أو or M ≫ m.هذة المقاربة هي معيار للكواكب التي تدور حول الشمس أو معظم الأقمار ويبسط إلى حد كبير المعادلات. وبموجب قانون الجذب العام لنيوتن، إذا كانت المسافة بين الاجسام r، فإن القوة التي تمارس على الجسم الأصغر هي:
وبالتالي فإن حاصل ضرب G و M مطلوب فقط للتنبؤ بحركة الجسم الأصغر. وعلى العكس من ذلك، لا توفر قياسات مدار الجسم الأصغر سوى معلومات عن ناتج μ، وليس G و M على حدة. وثابت الجاذبية، G، من الصعب قياس قيمتة بدقة عالية،[10] بينما يمكن قياس المدارات، على الأقل في النظام الشمسي، بدقة كبيرة وتستخدم لتحديد قيمة μ بدقة مماثلة.
مراجع
- "Astrodynamic Constants". ناسا/JPL. 27 February 2009. مؤرشف من الأصل في 21 مارس 201927 يوليو 2009.
- "Mars Gravity Model 2011 (MGM2011)". Western Australian Geodesy Group. مؤرشف من الأصل في 8 يوليو 2016.
- "Asteroid Ceres P_constants (PcK) SPICE kernel file". مؤرشف من الأصل في 31 مارس 201905 نوفمبر 2015.
- E.V. Pitjeva (2005). "High-Precision Ephemerides of Planets — EPM and Determination of Some Astronomical Constants" ( كتاب إلكتروني PDF ). Solar System Research. 39 (3): 176. Bibcode:2005SoSyR..39..176P. doi:10.1007/s11208-005-0033-2. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 7 سبتمبر 2012.
- D. T. Britt; D. Yeomans; K. Housen; G. Consolmagno (2002). "Asteroid density, porosity, and structure". In W. Bottke; A. Cellino; P. Paolicchi; R.P. Binzel (المحررون). Asteroids III. University of Arizona Press. صفحة 488. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 01 يونيو 2017.
- R.A. Jacobson; J.K. Campbell; A.H. Taylor; S.P. Synnott (1992). "The masses of Uranus and its major satellites from Voyager tracking data and Earth-based Uranian satellite data". المجلة الفلكية. 103 (6): 2068–2078. Bibcode:1992AJ....103.2068J. doi:10.1086/116211.
- M.W. Buie; W.M. Grundy; E.F. Young; L.A. Young; et al. (2006). "Orbits and photometry of Pluto's satellites: Charon, S/2005 P1, and S/2005 P2". المجلة الفلكية. 132: 290. arXiv:. Bibcode:2006AJ....132..290B. doi:10.1086/504422.
- M.E. Brown; E.L. Schaller (2007). "The Mass of Dwarf Planet Eris". ساينس. 316 (5831): 1586. Bibcode:2007Sci...316.1585B. doi:10.1126/science.1139415. PMID 17569855.
- يعود ذلك في الغالب إلى أن μ يمكن قياسها بواسطة علم الفلك الرصدي فقط كما هو الحال لعدة قرون.وتقسيمها إلى G وM يجب أن يتم عن طريق قياس قوة الجاذبية في شروط المختبر الدقيقة، كما حدث لأول مرة في تجربة كافنديش
- George T. Gillies (1997), "The Newtonian gravitational constant: recent measurements and related studies", Reports on Progress in Physics, 60, صفحات 151–225, Bibcode:1997RPPh...60..151G, doi:10.1088/0034-4885/60/2/001, مؤرشف من الأصل في 13 ديسمبر 2019 . A lengthy, detailed review.
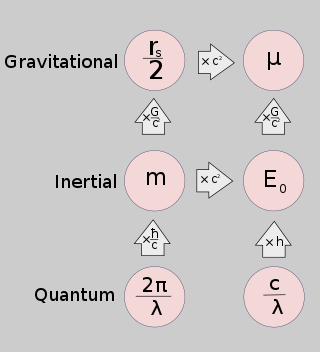
- نصف قطر شفارتزشيلد (rs) يمثل قدرة الكتلة على إحداث انحناء في الزمان والمكان.
- معامل الجاذبية القياسي (μ) يمثل قدرة الأجسام الضخمة لممارسة قوى الجاذبية النيوتونية على الأجسام الأخرى.
- الكتلة العطالية (m) تمثل الاستجابة النيوتونية للكتلة للقوى .
- الطاقة الساكنة (E0) تمثل قدرة تحول الكتلة إلى أشكال أخرى من الطاقة.
- طول موجة كومبتون (λ) يمثل الاستجابة الكمية للكتلة للهندسة المحلية (المكانية).

