الرئيسيةعريقبحث

تسلسل زمني لحساب ط

☰ جدول المحتويات

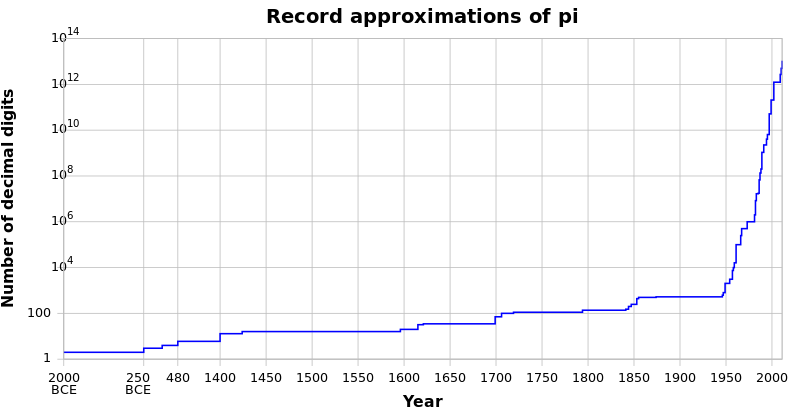
الجدول أسفله يبين التسلسل الزمني لحساب قيمة العدد باي.

مبيان يمثل عدد الرتب العشرية للعدد باي على مر الزمن

قبل 1400

تاريخ من الطريقة قيمة باي عدد الرتب العشرية (الأرقام القياسية مضغوطة)
2000? BCE المصريون القدماء[1] 4 × (8 / 9)2 3.16045... 1
2000? BCE البابليون القدماء[1] 3 + 1 / 8 3.125 1
1200? BCE الصين[1] 3 0
550? BCE الكتاب المقدس[1] "وعمل البحر مسبوكا عشر أذرع من شفته إلى شفته وكان مدورا مستديرا ارتفاعه خمسة أذرع وخيط ثلاثون ذراعا يحيط به بدائره " 3 0
434 BCE أناكساغوراس حاول تربيع الدائرة[2] الفرجار والمسطرة أناكساغوراس لم يعط أي حل 0
350? BCE سولبا سوترا[3][4] (6 / (2 + √2))2 3.088311 … 0
c. 250 BCE أرخميدس[1] 223 / 71 < π < 22 / 7 3.140845... < π < 3.142857...
3.1418 (ave.)		 3
15 BCE فيتروفيو[3] 25 / 8 3.125 1
5 ليو شين[3] the exact method is unknown 3.1457 2
130 زانغ هنغ (كتاب هان اللاحق)[1] √10 = 3.162277...
730/232 		3.146551... 2
150 بطليموس[1] 377 / 120 3.141666... 3
250 وانغ فان[1] 142 / 45 3.155555... 1
263 ليو هوي[1] 3.141024 < π < 3.142074
3927 / 1250 		3.14159 5
400 هي شينغتيان[3] 111035 / 35329 3.142885... 2
480 زو تشونغزي[1] 3.1415926 < π < 3.1415927
Zu's ratio 355 / 113 		3.1415926 7
499 أريابهاتا[1] 62832 / 20000 3.1416 3
640 براهماغوبتا[1] √10 3.162277... 1
800 الخوارزمي[1] 3.1416 3
1150 باسكارا الثاني[3] 3927 / 1250 and 754 / 240 3.1416 3
1220 فيبوناتشي[1] 3.141818 3
1320 زاو يوقين[3] 3.1415926 7

منذ 1400

التاريخ من ملحوظة عدد الرتب العشرية (الأرقام القياسية مضغوطة)
All records from 1400 onwards are given as the number of correct decimal places.
1400 مادهافا السنغماري Probably discovered the infinite متسلسلة قوى expansion of π,
now known as the صيغة لايبنتس ل π[5]		 10
1424 جمشيد الكاشي[6] 16
1573 فالنتينوس أوثو 355/113 6
1579 فرانسكوا فييت[7] 9
1593 أدريان فان رومن[8] 15
1596 لودولف فان ساولن 20
1615 32
1621 ويلبرورد سنيليوس تلميذ فان ساولن 35
1630 كريستوف غرينبرغر[9][10] 38
1665 إسحاق نيوتن[1] 16
1681 سيكي تاكاكازو[11] 11
16
1699 أبراهام شارب[1] حسب باي إلى 72 رتبة عشرية، لكن لم تكن كلها صحيحة 71
1706 جون ماكن[1] 100
1706 وليام جونز أول من استخدم الحرف الإغريقي π
1719 طوماس فانتي دو لاغني[1] حسب 127 رتبة عشرية، لكن ليست كلها صحيحة 112
1722 توشيكيو كاماتا 24
1722 تاكيبي كينكو 41
1739 Yoshisuke Matsunaga 51
1748 ليونهارد أويلر استخدم الحرف 'π' في كتابه Introductio in Analysin Infinitorum وضمن بذلك شهرته.
1761 يوهان لامبرت برهن على أن π عدد لاجذري
1775 أويلر قال أن العدد π ربما يكون عددا متساميا
1789 يوري فيجا حسب 143 رتبة عشرية، لكنها لم تكن كلها صحيحة 126
1794 يوري فيجا[1] حسب 140 رتبة عشرية، لكنها لم تكن كلها صحيحة 136
1794 أدريان ماري ليجاندر برهن على أن ²π عدد لاجذري
Late 18th century Anonymous manuscript Turns up at Radcliffe Library, in Oxford, England, discovered by F. X. von Zach, giving the value of pi to 154 digits, 152 of which were correct 152
1824 وليام رذرفورد[1] حسب 208 رتبة عشرية، لكنها لم تكن كلها صحيحة 152
1844 زكرياء دايز وسترانيتزكي[1] حسب 205 رتبة عشرية، لكنها لم تكن كلها صحيحة 200
1847 طوماس كلوسن[1] حسب 250 رتبة عشرية، لكنها لم تكن كلها صحيحة 248
1853 ليهمان[1] 261
1853 رذرفورد[1] 440
1874 وليام شانكس[1] استغرق 15 سنة لحساب 707 رتبة عشرية، لكنها لم تكن كلها صحيحة 527
1882 فرديناند فون ليندمان برهن على أن π عدد متسامي (مبرهنة ليندمان-ويرستراس)
1897 ولاية إنديانا كلنت على وشك تحديد قيمة 3.2 للعدد π[12] 1
1910 سرينفاسا أينجار رامانجن وجد عدة متسلسلات لحساب π والتي تعطي 8 رتب جديدة في كل حد.
1946 D. F. Ferguson Desk calculator 620
1947 إيفان نيفن أعطى برهانا بسيطا جدا على أن π عدد لاجذري
January 1947 D. F. Ferguson Desk calculator 710
September 1947 D. F. Ferguson Desk calculator 808
1949 D. F. Ferguson وجون رنش Desk calculator 1,120

عصر الحواسيب الإلكترونية (منذ 1949)

التاريخ من Implementation الوقت عدد الرتب العشرية (الأرقام القياسية مضغوطة)
All records from 1949 onwards were calculated with electronic computers.
1949 جون رنش, and L. R. Smith Were the first to use an electronic computer (the إينياك) to calculate π (also attributed to Reitwiesner et al.) [13] 70 hours 2,037
1953 كورت ماهلر Showed that π is not a عدد ليوفيل
1954 S. C. Nicholson & J. Jeenel Using the NORC [14] 13 minutes 3,093
1957 George E. Felton فيرانتي Pegasus computer (London), calculated 10,021 digits, but not all were correct [15] 7,480
January 1958 Francois Genuys IBM 704 [16] 1.7 hours 10,000
May 1958 George E. Felton Pegasus computer (London) 33 hours 10,021
1959 Francois Genuys IBM 704 (Paris)[17] 4.3 hours 16,167
1961 Daniel Shanks and جون رنش IBM 7090 (New York)[18] 8.7 hours 100,265
1961 J.M. Gerard IBM 7090 (London) 39 minutes 20,000
1966 Jean Guilloud and J. Filliatre IBM 7030 (Paris) 28 hours 250,000
1967 Jean Guilloud and M. Dichampt سي دي سي 6600 (Paris) 28 hours 500,000
1973 Jean Guilloud and Martin Bouyer CDC 7600 23.3 hours 1,001,250
1981 Kazunori Miyoshi and ياسوماسا كانادا FACOM M-200 2,000,036
1981 Jean Guilloud Not known 2,000,050
1982 Yoshiaki Tamura MELCOM 900II 2,097,144
1982 Yoshiaki Tamura and ياسوماسا كانادا HITAC M-280H 2.9 hours 4,194,288
1982 Yoshiaki Tamura and ياسوماسا كانادا HITAC M-280H 8,388,576
1983 ياسوماسا كانادا, Sayaka Yoshino and Yoshiaki Tamura HITAC M-280H 16,777,206
October 1983 Yasunori Ushiro and ياسوماسا كانادا HITAC S-810/20 10,013,395
October 1985 Bill Gosper Symbolics 3670 17,526,200
January 1986 ديفيد اتش بيلي CRAY-2 29,360,111
September 1986 ياسوماسا كانادا, Yoshiaki Tamura HITAC S-810/20 33,554,414
October 1986 ياسوماسا كانادا, Yoshiaki Tamura HITAC S-810/20 67,108,839
January 1987 ياسوماسا كانادا, Yoshiaki Tamura, Yoshinobu Kubo and others NEC SX-2 134,214,700
January 1988 ياسوماسا كانادا and Yoshiaki Tamura HITAC S-820/80 201,326,551
May 1989 الأخوان شودنوفسكي CRAY-2 & IBM 3090/VF 480,000,000
June 1989 الأخوان شودنوفسكي IBM 3090 535,339,270
July 1989 ياسوماسا كانادا and Yoshiaki Tamura HITAC S-820/80 536,870,898
August 1989 الأخوان شودنوفسكي IBM 3090 1,011,196,691
19 November 1989 ياسوماسا كانادا and Yoshiaki Tamura HITAC S-820/80 1,073,740,799
August 1991 الأخوان شودنوفسكي Homemade parallel computer (details unknown, not verified) [19] 2,260,000,000
18 May 1994 الأخوان شودنوفسكي New homemade parallel computer (details unknown, not verified) 4,044,000,000
26 June 1995 ياسوماسا كانادا and Daisuke Takahashi HITAC S-3800/480 (dual CPU) [20] 3,221,220,000
1995 سيمون بلوف Finds a formula that allows the nth hexadecimal digit of pi to be calculated without calculating the preceding digits.
28 August 1995 ياسوماسا كانادا and Daisuke Takahashi HITAC S-3800/480 (dual CPU) [21] 4,294,960,000
11 October 1995 ياسوماسا كانادا and Daisuke Takahashi HITAC S-3800/480 (dual CPU) [22] 6,442,450,000
6 July 1997 ياسوماسا كانادا and Daisuke Takahashi HITACHI SR2201 (1024 CPU) [23] 51,539,600,000
5 April 1999 ياسوماسا كانادا and Daisuke Takahashi HITACHI SR8000 (64 of 128 nodes) [24] 68,719,470,000
20 September 1999 ياسوماسا كانادا and Daisuke Takahashi HITACHI SR8000/MPP (128 nodes) [25] 206,158,430,000
24 November 2002 ياسوماسا كانادا & 9 man team HITACHI SR8000/MPP (64 nodes), Department of Information Science at the جامعة طوكيو in طوكيو, اليابان [26] 600 hours 1,241,100,000,000
29 April 2009 Daisuke Takahashi et al. T2K Open Supercomputer (640 nodes), single node speed is 147.2 فلوبس, computer memory is 13.5 تيرابايت, Gauss–Legendre algorithm, Center for Computational Sciences at the جامعة تسوكوبا in تسوكوبا, اليابان[27] 29.09 hours 2,576,980,377,524
Date Who Implementation Time Decimal places
(رقم عالميs in bold)
All records from Dec 2009 onwards are calculated on home computers with commercially available parts.
31 December 2009 فابريس بيلارد
  • Core i7 CPU at 2.93 GHz
  • 6 GiB (1) of RAM
  • 7.5 TB of disk storage using five 1.5 TB hard disks (Seagate Barracuda 7200.11 model)
  • 64 bit Red Hat Fedora 10 distribution
  • Computation of the binary digits: 103 days
  • Verification of the binary digits: 13 days
  • Conversion to base 10: 12 days
  • Verification of the conversion: 3 days
  • Verification of the binary digits used a network of 9 Desktop PCs during 34 hours, Chudnovsky algorithm, see [28] for Bellard's homepage.[29]
 131 days 2,699,999,990,000
2 August 2010 Shigeru Kondo[30]
  • using y-cruncher[31] by Alexander Yee
  • the Chudnovsky algorithm was used for main computation
  • verification used the Bellard & Plouffe formulas on different computers, both computed 32 hexadecimal digits ending with the 4,152,410,118,610th.
  • with 2 x Intel Xeon X5680 @ 3.33 GHz – (12 physical cores, 24 hyperthreaded)
  • 96 GB DDR3 @ 1066 MHz – (12 × 8 GB – 6 channels) – Samsung (M393B1K70BH1)
  • 1 TB SATA II (Boot drive) – Hitachi (HDS721010CLA332), 3 × 2 TB SATA II (Store Pi Output) – Seagate (ST32000542AS) 16 x 2 TB SATA II (Computation) – Seagate (ST32000641AS)
  • Windows Server 2008 R2 Enterprise x64
  • Computation of binary digits: 80 days
  • Conversion to base 10: 8.2 days
  • Verification of the conversion: 45.6 hours
  • Verification of the binary digits: 64 hours (primary), 66 hours (secondary)
  • Verification of the binary digits were done simultaneously on two separate computers during the main computation.[32]
 90 days 5,000,000,000,000
17 October 2011 Shigeru Kondo[33]
  • using y-cruncher by Alexander Yee
  • Verification: 1.86 days and 4.94 days
 371 days 10,000,000,000,050
28 December 2013 Shigeru Kondo[34]
  • using y-cruncher by Alexander Yee
  • with 2 x Intel Xeon E5-2690 @ 2.9 GHz – (16 physical cores, 32 hyperthreaded)
  • 128 GB DDR3 @ 1600 MHz – 8 x 16 GB – 8 channels
  • Windows Server 2012 x64
  • Verification: 46 hours
 94 days 12,100,000,000,050
8 October 2014 "houkouonchi"[31]
  • using y-cruncher by Alexander Yee
  • with 2 x Xeon E5-4650L @ 2.6 GHz
  • 192 GB DDR3 @ 1333 MHz
  • 24 x 4 TB + 30 x 3 TB
  • Verification: 182 hours
 208 days 13,300,000,000,000
11 November 2016 Peter Trueb[35][36]
  • using y-cruncher by Alexander Yee
  • with 4 x Xeon E7-8890 v3 @ 2.50 GHz (72 cores, 144 threads)
  • 1.25 TB DDR4
  • 20 x 6 TB
  • Verification: 28 hours[37]
 105 days 22,459,157,718,361[38]

المراجع

  1. David H. Bailey, Jonathan M. Borwein, Peter B. Borwein & Simon Plouffe (1997). "The quest for pi" ( كتاب إلكتروني PDF ). Mathematical Intelligencer. 19 (1): 50–57. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 3 أبريل 2019.
  2. https://web.archive.org/web/20170205201450/http://www.math.rutgers.edu/~cherlin/History/Papers2000/wilson.html. مؤرشف من الأصل في 5 فبراير 2017.
  3. Ravi P. Agarwal, Hans Agarwal & Syamal K. Sen (2013). "Birth, growth and computation of pi to ten trillion digits". Advances in Difference Equations. 2013: 100. doi:10.1186/1687-1847-2013-100. مؤرشف من الأصل في 19 أبريل 2019.
  4. Mathematics in India - Kim Plofker - Google Books
  5. Bag, A. K. (1980). "Indian Literature on Mathematics During 1400–1800 A.D." ( كتاب إلكتروني PDF ). Indian Journal of History of Science. 15 (1): 86. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 9 مارس 2012. π ≈ 2,827,433,388,233/9×10−11 = 3.14159 26535 92222…, good to 10 decimal places.
  6. approximated 2π to 9 sexagesimal digits. Al-Kashi, author: Adolf P. Youschkevitch, chief editor: Boris A. Rosenfeld, p. 256 O'Connor, John J.; Robertson, Edmund F., "Ghiyath al-Din Jamshid Mas'ud al-Kashi", MacTutor History of Mathematics archive . Azarian, Mohammad K. (2010), "al-Risāla al-muhītīyya: A Summary", Missouri Journal of Mathematical Sciences 22 (2): 64–85.
  7. Viète, François (1579). Canon mathematicus seu ad triangula : cum adpendicibus (باللغة اللاتينية). مؤرشف من الأصل في 14 أغسطس 2017.
  8. Romanus, Adrianus (1593). Ideae mathematicae pars prima, sive methodus polygonorum (باللغة اللاتينية). مؤرشف من الأصل في 03 يناير 2020.
  9. Grienbergerus, Christophorus (1630). Elementa Trigonometrica ( كتاب إلكتروني PDF ) (باللغة اللاتينية). مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 01 فبراير 2014.
  10. Hobson, Ernest William (1913). "Squaring the Circle": a History of the Problem. صفحة 27. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 10 مارس 2016.
  11. Yoshio, Mikami; Eugene Smith, David (April 2004) [January 1914]. A History of Japanese Mathematics (الطبعة paperback). Dover Publications.  . مؤرشف من الأصل في 22 فبراير 2019.
  12. Lopez-Ortiz, Alex (February 20, 1998). "Indiana Bill sets value of Pi to 3". the news.answers WWW archive. Department of Information and Computing Sciences, Utrecht University. مؤرشف من الأصل في 06 أبريل 200701 فبراير 2009.
  13. G. Reitwiesner, "An ENIAC determination of Pi and e to more than 2000 decimal places," MTAC, v. 4, 1950, pp. 11–15"
  14. S. C, Nicholson & J. Jeenel, "Some comments on a NORC computation of x," MTAC, v. 9, 1955, pp. 162–164
  15. G. E. Felton, "Electronic computers and mathematicians," Abbreviated Proceedings of the Oxford Mathematical Conference for Schoolteachers and Industrialists at Trinity College, Oxford, April 8–18, 1957, pp. 12–17, footnote pp. 12–53. This published result is correct to only 7480D, as was established by Felton in a second calculation, using formula (5), completed in 1958 but apparently unpublished. For a detailed account of calculations of x see J. W. Wrench, Jr., "The evolution of extended decimal approximations to x," The Mathematics Teacher, v. 53, 1960, pp. 644–650
  16. F. Genuys, "Dix milles decimales de x," Chiffres, v. 1, 1958, pp. 17–22.
  17. This unpublished value of x to 16167D was computed on an IBM 704 system at the Commissariat à l'Energie Atomique in Paris, by means of the program of Genuys
  18. [1] "Calculation of Pi to 100,000 Decimals" in the journal Mathematics of Computation, vol 16 (1962), issue 77, pages 76–99. نسخة محفوظة 27 أغسطس 2017 على موقع واي باك مشين.
  19. Bigger slices of Pi (determination of the numerical value of pi reaches 2.16 billion decimal digits) Science News 24 August 1991 http://www.encyclopedia.com/doc/1G1-11235156.html
  20. ftp://pi.super-computing.org/README.our_last_record_3b
  21. ftp://pi.super-computing.org/README.our_last_record_4b
  22. ftp://pi.super-computing.org/README.our_last_record_6b
  23. ftp://pi.super-computing.org/README.our_last_record_51b
  24. ftp://pi.super-computing.org/README.our_last_record_68b
  25. ftp://pi.super-computing.org/README.our_latest_record_206b
  26. https://web.archive.org/web/20190608113447/http://www.super-computing.org/pi_current.html. مؤرشف من الأصل في 8 يونيو 2019.
  27. https://web.archive.org/web/20161113224051/http://www.hpcs.is.tsukuba.ac.jp/~daisuke/pi.html. مؤرشف من الأصل في 13 نوفمبر 2016.
  28. "Fabrice Bellard's Home Page". bellard.org. مؤرشف من الأصل في 05 مايو 201928 أغسطس 2015.
  29. ( كتاب إلكتروني PDF ) https://web.archive.org/web/20191001032714/https://bellard.org/pi/pi2700e9/pipcrecord.pdf. مؤرشف من الأصل ( كتاب إلكتروني PDF ) في 1 أكتوبر 2019.
  30. "PI-world". calico.jp. مؤرشف من الأصل في 27 نوفمبر 201628 أغسطس 2015.
  31. "y-cruncher – A Multi-Threaded Pi Program". numberworld.org. مؤرشف من الأصل في 08 أبريل 201928 أغسطس 2015.
  32. "Pi – 5 Trillion Digits". numberworld.org. مؤرشف من الأصل في 25 أكتوبر 201828 أغسطس 2015.
  33. "Pi – 10 Trillion Digits". numberworld.org. مؤرشف من الأصل في 01 أكتوبر 201828 أغسطس 2015.
  34. "Pi – 12.1 Trillion Digits". numberworld.org. مؤرشف من الأصل في 01 أكتوبر 201828 أغسطس 2015.
  35. "pi2e". pi2e.ch. مؤرشف من الأصل في 26 فبراير 201915 نوفمبر 2016.
  36. "y-cruncher – A Multi-Threaded Pi Program". numberworld.org. مؤرشف من الأصل في 08 أبريل 201915 نوفمبر 2016.
  37. "Hexadecimal Digits are Correct! – pi2e trillion digits of pi". pi2e.ch. مؤرشف من الأصل في 16 نوفمبر 201615 نوفمبر 2016.
  38. 22,459,157,718,361 is πe × 1012 rounded down.

مقالات ذات صلة

موسوعات ذات صلة :