توزيع لابلاس

☰ جدول المحتويات

**توزيع لابلاس**
دالة الكثافة الاحتمالية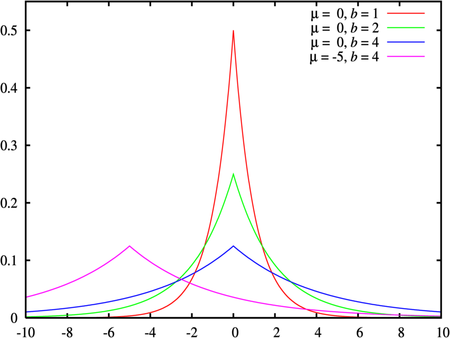
دالة التوزيع التراكمي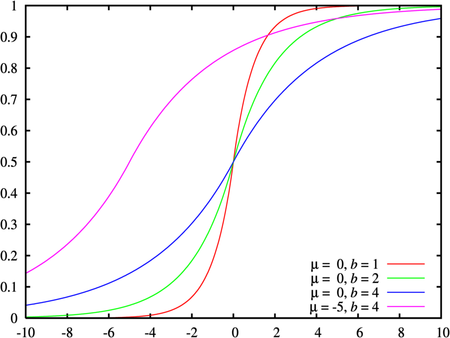
المؤشرات	$\mu \,$ موقع (حقيقي) $b>0\,$ (حقيقي)
الدعم	$x\in (-\infty ;+\infty )\,$
د۔ك۔ح۔	${\frac {1}{2\,b}}\exp \left(-{\frac {\|x-\mu \|}{b}}\right)\,$
د۔ت۔ت	انظر النص
المتوسط الحسابي	$\mu \,$
الوسيط الحسابي	$\mu \,$
المنوال	$\mu \,$
التباين	$2\,b^{2}$
التجانف	$0\,$
التفرطح	$3\,$
الاعتلاج	$\log(2\,e\,b)$
د۔م۔ع	${\frac {\exp(\mu \,t)}{1-b^{2}\,t^{2}}}\,\!$ for $\|t\|<1/b\,$
الدالة المميزة	${\frac {\exp(\mu \,i\,t)}{1+b^{2}\,t^{2}}}\,\!$
معلومات فيشر	{{{معلومات فيشر}}}

يقال أن لمتغير لعشوائي ما أنه يتبع توزيع لابلاس إذا كانت دالة كثافته تعطى بالشكل التالي:

f(x|\mu ,b)={\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)\,\!

={\frac {1}{2b}}{\begin{cases}\exp \left(-{\frac {\mu -x}{b}}\right)&{\mbox{si }}x<\mu \\[8pt]\exp \left(-{\frac {x-\mu }{b}}\right)&{\mbox{si }}x\geq \mu \end{cases}}

دالة التوزيع التراكمي لمتغير عشوائي يتبع توزيع لابلاس تعطى بالشكل التالي:

$F(x)\,$	$=\int _{-\infty }^{x}\!\!f(u)\,\mathrm {d} u$
	$={\begin{cases}{\frac {1}{2}}\exp \left(-{\frac {\mu -x}{b}}\right)&{\mbox{si }}x<\mu \\[8pt]1-{\frac {1}{2}}\exp \left(-{\frac {x-\mu }{b}}\right)&{\mbox{si }}x\geq \mu \end{cases}}$
	$=0,5\,[1+\operatorname {sgn}(x-\mu )\,(1-\exp(-\|x-\mu \|/b))].$

ومقلوب دالة التوزيع هو:

F^{-1}(p)=\mu -b\,\operatorname {sgn}(p-0,5)\,\ln(1-2|p-0,5|).

Robert M. Norton (May 1984). "The Double Exponential Distribution: Using Calculus to Find a Maximum Likelihood Estimator". ذا أمريكان ستاتيستيشين. American Statistical Association. 38 (2): 135–136. doi:10.2307/2683252. JSTOR 2683252.
Minguillon, J.; Pujol, J. (2001). "JPEG standard uniform quantization error modeling with applications to sequential and progressive operation modes". Journal of Electronic Imaging. 10 (2): 475–485. doi:10.1117/1.1344592.
Kotz, Samuel; Kozubowski, Tomasz J.; Podgórski, Krzysztof (2001). The Laplace distribution and generalizations: a revisit with applications to Communications, Economics, Engineering and Finance. Birkhauser. صفحات 23 (Proposition 2.2.2, Equation 2.2.8). . مؤرشف من الأصل في 4 يونيو 2013.