عملية تبديلية

مثال يظهر العملية التبديلية على جمع (3+2 = 2+3)

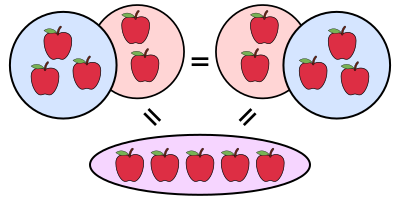
في الرياضيات، العملية التبديلية أو التبادلية (Commutativity)‏ هي قابلية العملية الرياضية على تبديل أماكن مدخلاتها دون تغير النتيجة.^[1][2][3] وهي من الخصائص الأساسية في العديد من فروع الرياضيات.

المعنى الرياضي

في الرياضيات, بخاصة الجبر التجريدي, تكون عملية ثنائية ما ${\displaystyle \times }$ معرفة على مجموعة S تبديلية إذا حققت الشرط التالي :

${\displaystyle x\times y=y\times x}$

أيا كان x وy ضمن المجموعة S. وإلا فإن العملية غير تبديلية.

عندئذ، يقال عن x وy أنهما متبادلان.

من أشهر العمليات التبديلية الجمع والضرب ضمن مجموعة الأعداد الحقيقية; مثلا:

• 4 + 5 = 5 + 4 (بما أن كلا التعبيرين مساويان ل 9)
• 2 × 3 = 3 × 2 (بما أن كلا التعبيرين مساويان ل 6)

من ضمن العمليات غير التبديلية, الطرح والقسمة والرفع إلى أس وتركيب الدوال (f o g), tetration (a↑↑b) وجداء المصفوفات.

أمثلة لعمليات تبديلية

• عملية التشفير وفك التشفير في أمن المعلومات الحاسوبية (تعدّ عملية تبديلية، حيث أن فك التشفير لا يهتم بترتيب التشفير، مثال على ذلك لعبة البوكر العقلية.
• ارتداء الحذاء يعتبر عملية تبديلية، لأنه لا يهم إن بدأت العملية بالقدم اليسرى أم اليمنى.

أمثلة لعمليات غير تبديلية

• عملية تبديل ترتيب الحروف في الكلمة الواحدة لا تعدّ عملية تبديلية، لأنه بتغير أماكن الحروف غالباً ما تنتج كلمة جديدة تختلف عن الكلمة الأصلية.
• عملية غسيل وتنشيف الملابس لا تعدّ عملية تبديلية، لأنه لا يمكن القيام بتنشيف الملابس قبل غسلها بل العكس هو الصحيح.

انظر أيضاً

• عملية ثنائية

مراجع

موسوعات ذات صلة :

• موسوعة جبر
• موسوعة رياضيات
• موسوعة الفيزياء