قانون باشن

منحنى باشن لعناصر الهيليوم والنيون والهيدروجين والنيتروجين.^[1]

قانون باشن (Paschen's law)‏ هو معادلة تعطي جهد الانهيار، أي الجهد اللازم لبدء التفريغ الشراري بين قطبين في غاز. يتناسب جهد الانهيار تناسبًا طرديًا مع حاصل ضرب ضغط الغاز في المسافة بين القطبين.^[2][3] سُميت باسم فريدريش باشن الذي اكتشفها تجريبيًا في عام 1889.^[4]

درس باشن جهد انهيار الغازات المختلفة بين ألواح معدنية متوازية حيث كان ضغط الغاز وحجم الفجوة بين القطبين متغيرين:

• انخفض الجهد اللازم للتفريغ الشراري عبر الفجوة عندما كان حجمها ثابتًا والضغط يتناقص تدريجيًا، وارتفع الجهد مرة أخرى مع تزايد الضغط تدريجيًا متجاوزًا قيمته الأصلية.
• انخفض الجهد اللازم للتفريغ الشراري مع تقليل حجم الفجوة لحد ما عند تثبيت الضغط، ومع تقليل حجم الفجوة أكثر؛ بدأ الجهد اللازم للتفريغ الشراري بالارتفاع وتجاوز قيمته الأصلية مرة أخرى.

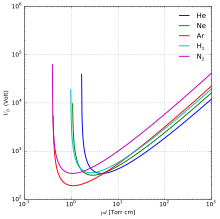
جهد الانهيار بالنسبة إلى غاز معين هو دالة حاصل ضرب ضغط الغاز في طول الفجوة. يطلق على منحنى الجهد مقابل حاصل ضرب طول الفجوة بالضغط «منحنى باشن»،^[3][2] وتُعرف المعادلة التي تلائم هذه المنحنيات بقانون باشن.^[3]

يكون جهد الانهيار متناسب تناسبًا طرديًا مع حاصل ضرب الضغط بطول الفجوة في الضغوط العالية وأطوال الفجوات الكبيرة، ويستخدم مصطلح قانون باشن أحيانًا للإشارة إلى هذه العلاقة الأكثر بساطة على مدى محدود من المنحنى.

منحنى باشن

وجدت التجارب على الخلاء (الفراغ) التي قام بها العلماء الأوائل سلوكًا مدهشًا، إذ يحدث القوس أحيانًا في مسار طويلٍ غير منتظم بدلًا من أقصر مسافة بين الأقطاب الكهربائية. في الهواء على سبيل المثال وعند ضغط واحد بار؛ تبلغ مسافة الحد الأدنى لجهد الانهيار نحو 7.5 ميكرومتر، ويبلغ جهد انهيار هذه المسافة 327 فولت، وهو غير كاف لإشعال الأقواس لفجوات أوسع أو أضيق. بالنسبة لفجوة 3.5 ميكرومتر، فإن الجهد المطلوب هو 533 فولت. إذا طُبِّقت 500 فولت فلن تكون كافية لإحداث قوس لفجوة 2.85 ميكرومتر، بل يجب أن تكون بطول 7.5 ميكرومتر.

وجد باشن أن جهد الانهيار يمكن وصفه بالمعادلة التالية:^[1]

${\displaystyle V_{\text{B}}={\frac {Bpd}{\ln(Apd)-\ln \left[\ln \left(1+{\frac {1}{\gamma _{\text{se}}}}\right)\right]}},}$

حيث:

• V هي جهد الانهيار، ويقاس بالفولت.

• p هو الضغط، ويقاس بالباسكال.

• d هي مقدار مسافة الفجوة، وتقاس بالمتر.

• ${\textstyle \gamma _{\text{se}}}$ معامل انبعاث الإلكترون الثانوي. (عدد الإلكترونات الثانوية المنبعثة بعد كل تصادم أيوني موجب)

• ${\displaystyle A}$تشبع التأين في الغاز عند قيمة نسبية للمجال الكهربائي إلى الضغط ${\displaystyle E/p}$.

• ${\displaystyle B}$ هي طاقة التأين والاستثارة.

يُحدَّد الثابتان (${\displaystyle A}$) و(${\displaystyle B}$) مخبريًا، وتبين أنهما تقريبًا ثابتان عند مدى قيم محدود لـ(E/p) لأي غاز. الرسم البياني لهذه المعادلة هو منحنى باشن، وعند اشتقاقها بالنسبة لـ(dp) وتعويض قيمتها بالصفر؛ فإنه يمكن تحديد الحد الأدنى لجهد الانهيار.^[5]

${\displaystyle pd={\frac {{e}\mathrm {\cdot } \ln {\mathrm {(} }{1}\mathrm {+} {\frac {1}{{\mathit {\gamma }}_{se}}}{\mathrm {)} }}{A}}}$

يُتوقع حدوث الحد الأدنى من جهد الانهيار عندما تكون ${\displaystyle pd}$= (7.5×10⁻⁶) بار. وهذه القيمة هي نفسها 327 فولت في الهواء عند الضغط الجوي القياسي عندما تكون الفجوة 7.5 ميكرومتر.

تُحدد مكوناتُ الغاز كلًا من الحد الأدنى لجهد الانهيار ومقدار حجم الفجوة. بالنسبة للأرغون؛ فإن جهد الانهيار هو 137 فولت عند 12 ميكرومتر. أما ثنائي أكسيد الكبريت؛ فيبلغ الحد الأدنى لجهد الانهيار 457 فولت عند 4.4 ميكرومتر فقط.

الفجوات الطويلة

يبلغ جهد الانهيار اللازم لفجوة طولها متر واحد في الهواء في الظروف القياسية من الضغط ودرجة الحرارة (درجة حرارة صفر مئوية، وضغط 1 بار) نحو 3.4 ميغا فولت.^[6] وبالتالي تبلغ شدة المجال الكهربائي لهذه الفجوة 3.4 ميغا فولت/متر. المجال الكهربائي اللازم لحدوث جهد انهيار عبر الحد الأدنى لفجوة أكبر بكثير من ما هو ضروري لفجوة مقدارها 1 متر. بالنسبة للفجوة 7.5 ميكرومتر، يكون جهد الانهيار 327 فولت، أي أن شدة المجال الكهربائي تساوي 43 ميغا فولت/متر، وهذا أكبر بنحو 13 مرة من شدة المجال لفجوة 1 متر. يجري التحقق بشكل جيد من هذه الظاهرة تجريبيًا ويشار إليها بأدنى قيمة لباشن. تفقد المعادلة دقتها مع الفجوات الأقل من 10 ميكرومتر في الهواء في ضغط جوي 1 بار، يمكن أن يختلف جهد الانهيار أيضًا عن تنبؤات منحنى باشن عند الفجوات الصغيرة جدًا للأقطاب الكهربائية.^[7]

الآلية الفيزيائية

المسار الحر الوسطي لجزيء ما في الغاز هو القيمة الوسطية للمسار الذي يقطعه جسيم (ذرة، فوتون، إلكترون،...) بين تصادمين متتاليين. وتتناسب هذه القيمة تناسبًا عكسيًا مع ضغط الغاز. يساوي المسار الحر الوسطي للجزيئات في الهواء عند 1 بار نحو 96 نانومتر. قيمة المسار الحر الوسطي للإلكترونات أطول بنحو 5.6 مرة أو 0.5 ميكرومتر لأن الإلكترونات أصغر بكثير، وهو الكسر مهم لفجوة 7.5 ميكرومتر بين الأقطاب الكهربائية لحدوث جهد التفريغ الشراري.

إذا كان الإلكترون في مجال كهربائي يبلغ 43 ميغا فولت/متر؛ فسيُسرَّع ويكتسب 21.5 إلكترون فولت من الطاقة في 0.5 ميكرومتر من المسار الذي يقطعه باتجاه المجال. إن طاقة التأين الأولى اللازمة لنزع إلكترون من جزيء النيتروجين تبلغ نحو 15.6 إلكترون فولت. سيكتسب الإلكترون المتسارع طاقة أكثر من كافية لتأيين جزيء النيتروجين، وسيُسرَّع هذا الإلكترون المحرّر ما سيؤدي إلى تصادم آخر، ثم يؤدي هذا التفاعل التسلسلي إلى انهيار في الجهد ويحدث قوس شراري من سلسلة الإلكترونات المتحررة هذه.^[8]

تحدث المزيد من التصادمات في مسار الإلكترون بين الأقطاب في الغاز ذو الضغط العالي. عندما يكون حاصل ضرب الفجوة بالضغط ${\displaystyle pd}$ مرتفعًا؛ سوف يصطدم الإلكترون بالعديد من جزيئات الغاز المختلفة أثناء انتقاله من المهبط إلى المصعد. كل التصادمات تُعشوئ اتجاه الإلكترون، لذلك لا يُسرَّع الإلكترون دائمًا بواسطة المجال الكهربائي - في بعض الأحيان ينتقل إلى المهبط ويتباطأ بفعل المجال. تقلل التصادمات طاقة الإلكترون وتجعل من الصعب عليها تأيين جزيء، تتطلب خسائر الطاقة الناتجة عن عدد أكبر من التصادمات فولتية أكبر للإلكترونات لتكديس طاقة كافية لتأيين الكثير من جزيئات الغاز، وهو أمر مطلوب لإنتاج انهيار في الجهد.

وعندما يكون حاصل ضرب الفجوة بالضغط (pd) صغيرًا؛ يمكن أن يصبح المسار الحر الوسطي للإلكترون طويلًا مقارنة بالفجوة بين الأقطاب الكهربائية، قد تكتسب الإلكترونات في هذه الحالة الكثير من الطاقة، ولكن لديها عدد أقل من التصادمات المؤينة، وبالتالي يلزم وجود جهد أكبر لضمان تأين جزيئات غاز كافية لبدء الانهيار.

تأثير غازات مختلفة

الغازات المختلفة سيكون لها مسارات حرة وسطية مختلفة للجزيئات والإلكترونات، وذلك لأن الجزيئات المختلفة لها أقطار مختلفة. الغازات النبيلة مثل الهيليوم والأرجون غازات أحادية الذرات وتميل لأن يكون لها أقطار أصغر، وهذا يعطيها أكبر مسارات حرة وسطية أكبر. تختلف إمكانيات التأين بين الجزيئات، وكذلك السرعة التي تستعيد بها الإلكترونات بعد خروجها من مدارها. تُغير هذه الآثار عدد التصادمات اللازمة للتسبب في نمو مُعتبر لعدد الإلكترونات الحرة الضرورية لإحداث القوس الشراري.

مقالات ذات صلة

• ضغط جوي
• جهد الانهيار
• شدة العزل

مراجع

موسوعات ذات صلة :

• موسوعة إلكترونيات
• موسوعة الفيزياء