متعددات الحدود لشيبيشيف

في الرياضيات، متعددات الحدود لشيبيشيف (Chebyshev polynomials)‏ هي متعددات حدود يعود اسمها إلى عالم الرياضيات الروسي بافنوتي تشيبيشيف,^[1] هي متتالية من متعددات حدود متعامدة لها صلة بصيغة دي موافر وتعرف ببساطة بواسطة ذاتية الاستدعاء.

عادة هناك فرق بين متعددات حدود شيبيشيف من النوع الأول والتي يرمز لها ب T_n وبين متعددات حدود شيبيشيف من النوع الثاني ويرمز لها U_n.

متعددات الحدود لشيبيشيف T_n أو U_n هي متعددات حدود من الدرجة n وتعاقب كثيرات حدود شيبيشيف لأي من النوعين تكون تعاقب كثيرات حدود.

متعددات حدود شيبيشيف مهمة في نظرية التقريب لأن جذور كثيرات حدود شيبيشيف ذات النوع الأول، والتي يطلق عليها أيضاً عقد شيبيشيف، تستخدم عقدا في استيفاء كثيرات الحدود.

في مجال المعادلات التفاضلية، تأتي متعددات الحدود لشيبيشيف حلحلة لمعادلة شيبيشيف.

${\displaystyle (1-x^{2})\,y''-x\,y'+n^{2}\,y=0\,\!}$

و

${\displaystyle (1-x^{2})\,y''-3x\,y'+n(n+2)\,y=0\,\!}$

(الصنف الأول حلحلة للمعادلة الأولى والثاني حلحلة للمعادلة الثانية). هاتان المعادلتان حالتان خاصتان من معادلة ستورم-ليوفيل التفاضلية.

تعريف

تعرف كثيرات حدود شيبيشيف من النوع الأول بالعلاقة التكرارية

${\displaystyle {\begin{aligned}T_{0}(x)&=1\\T_{1}(x)&=x\\T_{n+1}(x)&=2xT_{n}(x)-T_{n-1}(x).\end{aligned}}}$

وتكون الدالة المولدة التقليدية لـ T_n

${\displaystyle \sum _{n=0}^{\infty }T_{n}(x)t^{n}={\frac {1-tx}{1-2tx+t^{2}}}.\,\!}$

ودالة التوليد الأسية هي

${\displaystyle \sum _{n=0}^{\infty }T_{n}(x){\frac {t^{n}}{n!}}={1 \over 2}\left(e^{(x-{\sqrt {x^{2}-1}})t}+e^{(x+{\sqrt {x^{2}-1}})t}\right).\,\!}$

تعرف كثيرات حدود شيبيشيف من النوع الثاني بطريقة مشابهة

${\displaystyle {\begin{aligned}U_{0}(x)&=1\\U_{1}(x)&=2x\\U_{n+1}(x)&=2xU_{n}(x)-U_{n-1}(x).\end{aligned}}}$

من أمثلة الدوال المولدة لـ U_n

${\displaystyle \sum _{n=0}^{\infty }U_{n}(x)t^{n}={\frac {1}{1-2tx+t^{2}}}.\,\!}$

تعريف بالنسب المثلثية

النوع الأول:

${\displaystyle T_{n}(x)=\cos(n\arccos x)=\cosh(n\,\mathrm {arccosh} \,x)\,\!}$

حيث:

${\displaystyle T_{n}(\cos(\vartheta ))=\cos(n\vartheta )\,\!}$

لقيم n = 0, 1, 2, 3,..., أما النوع الثاني:

${\displaystyle U_{n}(\cos(\vartheta ))={\frac {\sin((n+1)\vartheta )}{\sin \vartheta }}\,\!}$

لهذه المتطابقة فائدة قصوى مع وجود صيغة التوليد التكرارية لأنها تسمح بحساب جيب التمام لأي تكامل من مضاعفات زاوية بدلالة جيب تمام الزاوية الأساسية.بتقييم كثيرتي حدود شيبيشف الأوليتين:

${\displaystyle T_{0}(x)=\cos \ 0x\ =1\,\!}$

و:

${\displaystyle T_{1}(\cos(x))=\cos(x)\,\!}$

يمكن بيان أن:

${\displaystyle \cos(2\vartheta )=2\cos \vartheta \cos \vartheta -\cos(0\vartheta )=2\cos ^{2}\,\vartheta -1\,\!}$

${\displaystyle \cos(3\vartheta )=2\cos \vartheta \cos(2\vartheta )-\cos \vartheta =4\cos ^{3}\,\vartheta -3\cos \vartheta \,\!}$

وهكذا.

تعريف معادلة بل

يمكن تعريف كثيرات حدود شيبيشف أيضاً بأنها حلول معادلة بل

${\displaystyle T_{i}^{2}-(x^{2}-1)U_{i-1}^{2}=1\,\!}$

في حلقة R[x].^[2] بالتالي، يمكن توليدها بالطريقة القياسية لمعادلات بل بأخذ قوى حل أساسي:

${\displaystyle T_{i}+U_{i-1}{\sqrt {x^{2}-1}}=(x+{\sqrt {x^{2}-1}})^{i}.\,\!}$

العلاقة بين كثيرات حدود شيبيشيف من النوع الأول والنوع الثاني

العلاقة متشابهة بين كثيرات حدود شيبيشيف من النوع الأول والنوع الثاني بالمعالات التالية

${\displaystyle {\tfrac {d}{dx}}\,T_{n}(x)=nU_{n-1}(x){\mbox{ , }}n=1,\ldots }$

${\displaystyle T_{n}(x)={\frac {1}{2}}(U_{n}(x)-\,U_{n-2}(x)).}$

${\displaystyle T_{n+1}(x)=xT_{n}(x)-(1-x^{2})U_{n-1}(x)\,}$

${\displaystyle T_{n}(x)=U_{n}(x)-x\,U_{n-1}(x).}$

العلاقة التكرارية لمشتقات كثيرات حدود شيبيشيف يمكن اشتقاقها من هذه العلاقات

${\displaystyle 2T_{n}(x)={\frac {1}{n+1}}\;{\frac {d}{dx}}T_{n+1}(x)-{\frac {1}{n-1}}\;{\frac {d}{dx}}T_{n-1}(x){\mbox{ , }}\quad n=1,\ldots }$

تستعمل هذه العلاقة في طريقة طيفية شيبيشيف لحل المعادلات التفاضلية.

بالمثل، يمكن تعريف التعاقبين من أزواج معادلات تكرار متبادل:

${\displaystyle T_{0}(x)=1\,\!}$

${\displaystyle U_{-1}(x)=0\,\!}$

${\displaystyle T_{n+1}(x)=xT_{n}(x)-(1-x^{2})U_{n-1}(x)\,}$

${\displaystyle U_{n}(x)=xU_{n-1}(x)+T_{n}(x)\,}$

صيغ صريحة

${\displaystyle T_{n}(x)={\begin{cases}\cos(n\arccos(x)),&\ x\in [-1,1]\\\cosh(n\,\mathrm {arccosh} (x)),&\ x\geq 1\\(-1)^{n}\cosh(n\,\mathrm {arccosh} (-x)),&\ x\leq -1\\\end{cases}}\,\!}$

${\displaystyle {\begin{aligned}T_{n}(x)&={\frac {(x-{\sqrt {x^{2}-1}})^{n}+(x+{\sqrt {x^{2}-1}})^{n}}{2}}\\&=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n}{2k}}(x^{2}-1)^{k}x^{n-2k}\\&=x^{n}\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n}{2k}}(1-x^{-2})^{k}\\&={\frac {n}{2}}\sum _{k=0}^{\lfloor n/2\rfloor }(-1)^{k}{\frac {(n-k-1)!}{k!(n-2k)!}}~(2x)^{n-2k}\quad (n>0)\\&=n\sum _{k=0}^{n}(-2)^{k}{\frac {(n+k-1)!}{(n-k)!(2k)!}}(1-x)^{k}\quad (n>0)\\&=\,_{2}F_{1}\left(-n,n;{\frac {1}{2}};{\frac {1-x}{2}}\right)\\\end{aligned}}}$

${\displaystyle {\begin{aligned}U_{n}(x)&={\frac {(x+{\sqrt {x^{2}-1}})^{n+1}-(x-{\sqrt {x^{2}-1}})^{n+1}}{2{\sqrt {x^{2}-1}}}}\\&=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n+1}{2k+1}}(x^{2}-1)^{k}x^{n-2k}\\&=x^{n}\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n+1}{2k+1}}(1-x^{-2})^{k}\\&=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {2k-(n+1)}{k}}~(2x)^{n-2k}\quad (n>0)\\&=\sum _{k=0}^{\lfloor n/2\rfloor }(-1)^{k}{\binom {n-k}{k}}~(2x)^{n-2k}\quad (n>0)\\&=\sum _{k=0}^{n}(-2)^{k}{\frac {(n+k+1)!}{(n-k)!(2k+1)!}}(1-x)^{k}\quad (n>0)\\&=(n+1)\,_{2}F_{1}\left(-n,n+2;{\frac {3}{2}};{\frac {1-x}{2}}\right)\end{aligned}}}$

حيث ${\displaystyle _{2}F_{1}}$ هي دالة مثلثية زائدية.

الخواص

التحويل

من المتطابقات المفيدة في تحويل كثيرات الحدود

${\displaystyle T_{n}\left(1-2x^{2}\right)=(-1)^{n}T_{2n}(x)}$

و

${\displaystyle U_{n}\left(1-2x^{2}\right)x=(-1)^{n}U_{2n+1}(x).}$

الجذور والقيم القصوى

لأي من النوعين في كثيرات حدود شيبيشف من الدرجة n يوجد لها n جذور بسيطة مختلفة تدعى جذور شيبيشف في الفترة [−1,1]. باستعمال التعريف المثلثي والحقيقة القائلة بأن

${\displaystyle \cos \left({\frac {\pi }{2}}\,(2k+1)\right)=0}$

يمن إثبات أن جذور T_n هي

${\displaystyle x_{k}=\cos \left({\frac {\pi }{2}}\,{\frac {2k-1}{n}}\right),\quad k=1,\ldots ,n.}$

بالمثل جذور U_n هي

${\displaystyle x_{k}=\cos \left({\frac {k}{n+1}}\pi \right),\quad k=1,\ldots ,n.}$

التفاضل والتكامل

باشتقاق كثيرات الحدود في صورها المثلثية، يمكن بسهولة الوصل لايلي:

${\displaystyle {\frac {dT_{n}}{dx}}=nU_{n-1}\,}$

${\displaystyle {\frac {dU_{n}}{dx}}={\frac {(n+1)T_{n+1}-xU_{n}}{x^{2}-1}}\,}$

${\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}=n{\frac {nT_{n}-xU_{n-1}}{x^{2}-1}}=n{\frac {(n+1)T_{n}-U_{n}}{x^{2}-1}}.\,}$

التعامدية

إن كلا من T_n وU_n تكونان تعاقب كثيرات حدود متعامدة. كثيرات الحدود من النوع الأول تكون متعامدة بالنسبة للوزن

${\displaystyle {\frac {1}{\sqrt {1-x^{2}}}},\,\!}$

في الفترة (−1,1), أي أن:

${\displaystyle \int _{-1}^{1}T_{n}(x)T_{m}(x)\,{\frac {dx}{\sqrt {1-x^{2}}}}={\begin{cases}0&:n\neq m\\\pi &:n=m=0\\\pi /2&:n=m\neq 0\end{cases}}}$

بالمثل، كثيرات الحدود من النوع الثاني تكون متعامدة بالنسبة للوزن

${\displaystyle {\sqrt {1-x^{2}}}\,\!}$

على الفترة [−1,1], أي أن:

${\displaystyle \int _{-1}^{1}U_{n}(x)U_{m}(x){\sqrt {1-x^{2}}}\,dx={\begin{cases}0&:n\neq m,\\\pi /2&:n=m.\end{cases}}}$

الأصغرية ∞-طبيعي

لأي قيمة n ≥ 1, بين كثيرات الحدود من الدرجة nمع معامل أسبقية 1,

${\displaystyle f(x)={\frac {1}{2^{n-1}}}T_{n}(x)}$

هي تلك التي لها قيمة مطلقة أعظمية في الفترة [−1, 1] تكون أصغرية.

هذه القيمة الأعظمية تكون

${\displaystyle {\frac {1}{2^{n-1}}}}$

و|ƒ(x)| تصل لهذه القيمة العظمى تماماً n + 1 من المرات: عند

${\displaystyle x=\cos {\frac {k\pi }{n}}{\text{ for }}0\leq k\leq n.}$

صلتها بكثيرات حدود أخرى

• ${\displaystyle T_{n}(x)={\frac {1}{n-{\frac {1}{2}} \choose n}}P_{n}^{-{\frac {1}{2}},-{\frac {1}{2}}}(x)={\frac {n}{2}}C_{n}^{0}(x),}$
• ${\displaystyle U_{n}(x)={\frac {1}{2{n+{\frac {1}{2}} \choose n}}}P_{n}^{{\frac {1}{2}},{\frac {1}{2}}}(x)=C_{n}^{1}(x).}$

أمثلة

بعض من كثيرات حدود شيبيشف الأولى من النوع الأول في المجال −1 < x < 1: الأسطح T₀, T₁, T₂, T₃, T₄ وT₅.

بعض كثيرات حدود شيبيشف الأولى من النوع الأول هي

${\displaystyle T_{0}(x)=1\,}$

${\displaystyle T_{1}(x)=x\,}$

${\displaystyle T_{2}(x)=2x^{2}-1\,}$

${\displaystyle T_{3}(x)=4x^{3}-3x\,}$

${\displaystyle T_{4}(x)=8x^{4}-8x^{2}+1\,}$

${\displaystyle T_{5}(x)=16x^{5}-20x^{3}+5x\,}$

${\displaystyle T_{6}(x)=32x^{6}-48x^{4}+18x^{2}-1\,}$

${\displaystyle T_{7}(x)=64x^{7}-112x^{5}+56x^{3}-7x\,}$

${\displaystyle T_{8}(x)=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1\,}$

${\displaystyle T_{9}(x)=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x.\,}$

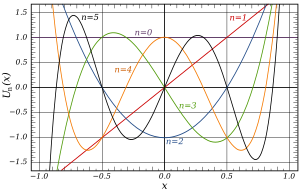
بعض من كثيرات حدود شيبيشف الأولى من النوع الثاني في المجال −1 < x < 1: الأسطح U₀, U₁, U₂, U₃, U₄ وU₅.

بعض كثيرات حدود شيبيشف الأولى من النوع الثاني هي

${\displaystyle U_{0}(x)=1\,}$

${\displaystyle U_{1}(x)=2x\,}$

${\displaystyle U_{2}(x)=4x^{2}-1\,}$

${\displaystyle U_{3}(x)=8x^{3}-4x\,}$

${\displaystyle U_{4}(x)=16x^{4}-12x^{2}+1\,}$

${\displaystyle U_{5}(x)=32x^{5}-32x^{3}+6x\,}$

${\displaystyle U_{6}(x)=64x^{6}-80x^{4}+24x^{2}-1\,}$

${\displaystyle U_{7}(x)=128x^{7}-192x^{5}+80x^{3}-8x\,}$

${\displaystyle U_{8}(x)=256x^{8}-448x^{6}+240x^{4}-40x^{2}+1\,}$

${\displaystyle U_{9}(x)=512x^{9}-1024x^{7}+672x^{5}-160x^{3}+10x.\,}$

كمجموعة أساسات

في فضاء سوبوليف, تؤلف مجموعة كثيرات حدود شيبيشف مجموعة أساسمكتملة بحيث أن دالة في نفس الفضاء يمكن التعبير عنها على −1 ≤ x ≤ 1 بالنشر:^[3]

${\displaystyle f(x)=\sum _{n=0}^{\infty }a_{n}T_{n}(x).}$

مثال 1

ليكن لدينا منشور شيبيشيف ${\displaystyle \log(1+x)}$. يمكن التعبير عنه

${\displaystyle \log(1+x)=\sum _{n=0}^{\infty }a_{n}T_{n}(x).}$

كما يمكن إيجاد المعاملات ${\displaystyle a_{n}}$ إما بتطبيق الضرب الداخلي أو من شرط التعامدية المتقطعة. بطريقة الضرب الداخلي

${\displaystyle \int _{-1}^{+1}{\frac {T_{m}(x)\log(1+x)}{\sqrt {1-x^{2}}}}dx=\sum _{n=0}^{\infty }a_{n}\int _{-1}^{+1}{\frac {T_{m}(x)T_{n}(x)}{\sqrt {1-x^{2}}}}dx,}$

نحصل على

${\displaystyle a_{n}={\begin{cases}-\log(2)&:n=0\\{\frac {-2(-1)^{n}}{n}}&:n>0.\end{cases}}}$

بالمثل وعند عدم جدوى طريقة الضرب الداخلي نلجأ لطريقة شرط التعامدية المتقطعة فنحصل على

${\displaystyle a_{n}={\frac {2-\delta _{0n}}{N}}\sum _{k=0}^{N-1}T_{n}(x_{k})\log(1+x_{k}),}$

حيث ${\displaystyle \delta _{ij}}$ هي دالة دلتا كرونكر و${\displaystyle x_{k}}$ هي N أصفار ${\displaystyle T_{N}(x)}$ من غاوس–لوباتو

${\displaystyle x_{k}=\cos \left({\frac {\pi \left(k+{\frac {1}{2}}\right)}{N}}\right).}$

وبحساب المعاملات ${\displaystyle a_{n}}$ بواسطة تحويل جيب التمام المتقطع

${\displaystyle a_{n}={\frac {2-\delta _{0n}}{N}}\sum _{k=0}^{N-1}\cos \left({\frac {n\pi \left(k+{\frac {1}{2}}\right)}{N}}\right)\log(1+x_{k}).}$

مثال 2

${\displaystyle {\begin{aligned}(1-x^{2})^{\alpha }=&-{\frac {1}{\sqrt {\pi }}}{\frac {\Gamma ({\frac {1}{2}}+\alpha )}{\Gamma (\alpha +1)}}+2^{1-2\alpha }\sum _{n=0}(-1)^{n}{2\alpha \choose \alpha -n}T_{2n}(x)\\=&2^{-2\alpha }\sum _{n=0}(-1)^{n}{2\alpha +1 \choose \alpha -n}U_{2n}(x).\end{aligned}}}$

مقالات ذات صلة

• متعددات الحدود لهيرمت
• نظرية التقريب
• تباين الأخوين ماركوف

مراجع

موسوعات ذات صلة :

• موسوعة رياضيات