هندسة كسيرية

الكُسيريات أو الفركتلات (Fractals)‏ هي أشكال هندسية تختلف عن الأشكال الهندسية الأخرى بسبب الطريقة التي تتدرج بها زيادة أو نقصانا. مضاعفة أطوال حافة مضلع يضاعف لها المساحة إلى أربعة، وهو اثنان (النسبة بين الطول الجديد إلى طول الجانب القديم) مرفوعا للقوة (أس) اثنين ( مساحة المضلع ). وبالمثل، إذا تضاعف نصف قطر الكرة، فإن حجم الكرة يقفز إلى ثمانية أضعاف، والتي هي اثنين (نسبة القطر الجديد إلى القديم) مرفوعا إلى القوة ثلاثة (المساحة التي تشغلها الكرة). ولكن إذا تم مضاعفة الأطوال الفركتلية ذات البعد الواحد فقط، فإن المحتوى المكاني للجداول الكسورية من قبل الأس الذي ليس بالضرورة أن يكون واحدا صحيح.^[1] وتسمى هذه القوة أو الأس البعد كسيري للفراكتل، وعادة ما يتجاوز البعد الطوبوغرافي الكسوري .^[2]

مثل المعادلات الرياضية، فإن الفركتلات عادة ما تكون قابلة للاشتقاق أي مكان.^[1] ويمكن تصور المنحنى الكسورية اللانهائي بأنه يكون ملتفا عبر الفضاء بشكل مختلف عن الخط العادي، لا يزال كونه مساحة ذات البعد الواحد وهو الخط لديه بعدا كسوريا مشيرا إلى أنه يشبه أيضا سطح.^[1][2]

جذور فكرة رياضية تم الرجوع إلى مفهوم الفركتلات على مر السنين كمسار رسمي من المصنفات المنشورة، بدءا من القرن ال17 مع مفاهيم استدعاء ذاتي، ثم تتحرك من خلال معالجة رياضية صارمة لمفهوم دراسة متواصلة ولكن ليست دالة قابلة للاشتقاق في القرن ال19، وإلى صياغة لل كلمة كسورية في القرن ال20 مع ازدهار لاحق من الاهتمام في فركتلات والنمذجة القائم على الحاسوب في القرن ال21. وقد استخدم مصطلح "كسورية" أول مرة من قبل عالم الرياضيات بونوا ماندلبرو في عام 1975. ماندلبروت قام باشتقاقها مناللاتينية frāctus تعني "كسر" أو "متشظية "، وتستخدم لتوسيع المفهوم النظري كسور البعد إلى أنماط هندسية في الطبيعة.^[1]

زربية سيربنسكي animation. Interations for this famous two-dimensional fractal.

مجموعة ماندلبروت, التي سميت على اسم مكتشفها، هي أهم مثال عن البنى الكسيرية

مجموعة جوليا التي تحمل اسم مكتشفها غاستون جوليا

تدرس الهندسة الكسيرية (Fractal Geometry أو Fractals)‏ البنى الهندسية المؤلفة من كسيريات وهو مجموع كسيرية Fractals التي يمكن تعريفها بأنها جزء هندسي صغير جدا غير منتظم ذو أبعاد لامتناهية بالصغر، يمكن أن يتألف من أجزاء متشابهة مؤلفة بدورها من أجزاء متشابهة مشابهة للجزء الأم.

الكسيرية إذا يمكن تعريفها على أنها كائن هندسي خشن غير منتظم على كافة المستويات، ويمكن تمثيلها بعملية كسر شيء ما إلى أجزاء أصغر لكن هذه الأجزاء تشابه الجسم الأصلي. تحمل الكسيرية في طياتها ملامح مفهوم اللانهاية وتتميز بخاصية التشابه الذاتي أي أن مكوناتها مشابهة للكسيرية الأم مهما كانت درجة التكبير. غالبا ما يتم تشكيل الأجسام الكسيرية عن طريق عمليات أو خوارزميات متكررة: مثل العمليات الذاتية الاستدعاء أو التكرارية.

الكسيرية هي مجموعة لها بُعد كسيري عادة ما يتجاوز بعدها الطوبولوجي.

تمت صياغة مصطلح كسيرية (fractal) من قبل بونوا ماندلبرو، من اللاتينية fractus بمعنى مكسور. كان ذلك عام 1975. قبل هذا المصطلح كان الاسم الشائع لهذه البنى هو ندفة الثلج لكوخ. تقوم الهندسة الكسيرية عادة بدراسة البنى المؤلفة من كسيريات وتصف العديد من الأوضاع والبنى التي لا يمكن تفسيرها أو دراستها بالهندسة الرياضية الكلاسيكية، إضافة لذلك تمتلك الهندسة الكسيرية تطبيقات عديدة في العلوم والتكنولوجيا والفنون الحاسوبية.

الكسيرية

مخطط ندفة الثلج لكوخ

الكسيرية كائن هندسي يتصف بالخشونة وعدم الانتظام على كل المقاييس، ولهذا يبدو في جوهره وكأنه 'مكسور'. ببساطة، يمكن تعريف الكسيريات على أنها صور مقسمة إلى أجزاء، كل منها يبدو مماثلاً للأصل. تحتوي الكسيريات في طياتها معنى اللانهاية، ويبدي بعضها بنية تتصف بالتشابه الذاتي على كل المقاييس، ومختلف مستويات التكبير. في معظم الحالات، يمكن توليد الكسيريات من خلال تكرار معين، يتم ذلك عبر إجراء تعاودي أو تكراري. قبل أن يقوم ماندلبروت بصياغة هذا المصطلح، كان الاسم الشائع لهذه البنى (كندفة الثلج لكوخ مثلاً) هو المنحني الغريب monster curve.

تمت دراسة العديد من أنواع الكسيريات على أنها كائنات رياضية. تشكل الهندسة الكسيرية فرعاً من الرياضيات يختص بدراسة سلوك وخصائص الكسيريات، كما تصف الكثير من الحالات التي يستعصي وصفها على الهندسة الكلاسيكية، وغالباً ما تطبق في حقول العلوم والتكنولوجيا والفنون المولدة حاسوبياً. إن تتبع الجذور المفاهيمية للكسيريات يقود إلى محاولات سابقة لقياس أغراض عجزت التعاريف التقليدية للهندسة الإقليدية والحساب الإقليدي عن شرحها.

تاريخ الكسيريات

إسهامات التحليل الكلاسيكي

لقد اكتشفت الأغراض المسماة حالياً كسيريات ودُرست قبل زمن بعيد من إطلاق هذه التسمية عليها، فإشارة ماندلبروت ذاته إلى فكرة (التشابه الذاتي التعاودي) تعد تطويراً قام به الفيلسوف لايبنتز الذي تعمق في دراسة تفاصيل هذه الأغراض. في عام 1872، أوجد كارل ويرستراس مثالاُ لدالة ذات خاصية غريبة، ذلك أنها تستمر في كل مكان ولا يمكن تمييزها في أي مكان، إن مخطط هذه الدالة يدعى حالياً كسيرية. في عام 1904، اختلف هيلغ فون كوخ مع التعريف التحليلي المجرد لفايرستراس، وقدم تعريفاً ذا مضمون هندسي أكثر لدالة مشابهة تدعى حالياً ندفة الثلج لكوخ. إن فكرة المنحنيات ذات التشابه الذاتي طورت من قبل باول بيير ليفي والذي شرح عام 1938 في ورقة بحثه السطوح والمنحنيات المستوية أو الفراغية التي تشكل أجزاءً مشابهة للأصل منحنى كسيريا جديدا يدعى كسيرية ليفي. كما قدم جورج كانتور أمثلة لمجموعات جزئية من الخط الحقيقي تتصف بصفات غير طبيعية -إن مجموعات كانتور هذه تصنف حالياً ضمن الكسيريات. تمت دراسة التوابع التكرارية في المستوى العقدي في أواخر القرن التاسع عشر وبدايات القرن العشرين من قبل هنري بوانكاريه وفيليكس كلاين وبيير فاتو وغاستون جوليا. لسوء الحظ، فإن انعدام التقنيات المرئية الحاسوبية الشائعة حالياً في ذلك الوقت، حرم أولئك العلماء من إدراك المعنى الجمالي المرئي للعديد من الأغراض التي اكتشفوها.

مفاهيم لتوضيح مجموعة الكسيريات

في محاولة جادة لفهم أغراض معينة كمجموعات كانتور، عمد الرياضيون من أمثال كونسستانتين كاراثيودوري وفيليكس هاوسدورف إلى تعميم المفهوم الحدسي للبعد حيث يتضمن قيماً غير صحيحة. كانت هذه الخطوة جزءاً من توجه ساد في بدايات القرن العشرين بهدف تكوين نظرية وصفية للمجموعة، وكان هذا إتماماً لأبحاث كانتور والتي كانت قادرة إلى حد ما على تصنيف مجموعات من النقاط في فضاء إقليدي. إن تعريف بُعد هاوسدروف ذو طبيعة هندسية، ولو أنه شُكل تقنياً باستخدام أدوات من التحليل الرياضي. عمل بيزيكوفيتش في هذا الاتجاه على غرار الآخرين، وقد اختلف في مضمونه عن التحريات المنطقية التي بُني على أساسها القسم الأعظم من النظرية الوصفية للمجموعة على عشرينيات وثلاثينات القرن العشرين، وقد تمت متابعة الأبحاث لاحقاً في هذا المجال، ولكن من قبل المختصين حصراً.

إسهامات ماندلبروت في الستينيات

عمل بينويت ماندلبروت على استقصاء التشابه الذاتي، تجلى ذلك في بضعة أوراق نشرها مثل كم طول ساحل بريطانيا؟ التشابه الذاتي الإحصائي والبعد الكسيري، وقد بنى عمله على الأعمال السابقة للويس فراي ريتشاردسن. تمكن ماندلبروت من اكتشاف صلات قوية بين نتائج رياضية لطالما اعتبرت غير مترابطة سابقاً بفضل اعتماده وبشكل كبير على مقاربة مرئية. عام 1975، صاغ ماندلبروت كلمة كسيرية أو 'فركتل' 'fractal' للدلالة على أغراض ذات تشابه ذاتي، لا تمتلك بعداً محدداً. لقد اشتق كلمة كسيرية من الكلمة اللاتينية fractus والتي تعني 'مكسور' أو 'غير نظامي'، وليس من كلمة fractional والتي تعني كسري كما يظن الكثيرون، مع العلم أن هذه الأخيرة يعتقد أنها مشتقة أيضاً من كلمة fractus اللاتينية. لدى استخدام المرئيات الحاسوبية في مجال الهندسة الكسيرية، ظهرت براهين مرئية سرعان ما ربطت العديد من مجالات الرياضيات والعلوم بشكل غير مسبوق، تحديداً في حقول الديناميكية اللاخطية، نظرية الشواش (علماً أن البعض يفضل استخدام المصطلح xaos عوضاً عن السايقة وذلك بهدف التمييز بين السلوك اللاخطي والمعنى المتداول للكلمة) والتعقيد. فعلى سبيل المثال، أظهر رسم خوارزمية نيوتن بشكل كسيري أن الحدود بين الحلول المختلفة هي ذات طبيعة كسيرية، كما أظهرت أن الحلول بحد ذاتها هي جواذب غريبة. تستخدم الهندسة الكسيرية أيضاً في مجال ضغط البيانات ونمذجة الأنظمة الجيولوجية والعضوية المعقدة، يعد نمو الأشجار وتظور أحواض الأنهار أمثلة واضحة على ذلك. وسع هاريسون الحساب النيوتوني بشكل يتضمن المجالات الفركتلية، بما فيها نظريات غاوس وغرين وستوكس.

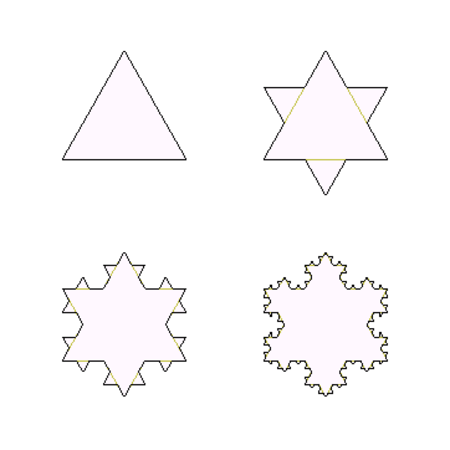
البعد الكسيري لحد ندفة ثلج كوخ

إن الطول الكلي لعدد ما N بالنسبة لمجموعة من الخطوات L هو الجداء NL، بتطبيق ذلك على حد ندفة ثلج كوخ سنحصل على طول لانهائي للحد ذلك أن L لامتناهية في الصغر، إن هذا غير مقبول، فكما أن ندف ثلج كوخ المختلفة لها قياسات مختلفة، فإن الحل هو بالقياس، ليس بالمتر ولا بالمتر المربع، بل باستخدام واحدة المتر مرفوعة إلى قوة على الشكل m². وبالتالي: 4N(L/3)^x = NL^x، نفسر العلاقة السابقة بأن تصغير طول الخطوة لثلاثة أمثال يتطلب أربعة أمثال عدد الخطوات، إن حل المعادلة السابقة يعطي x = (log 4)/(log 3) = 1.26186. وبالتالي فإن واحدة قياس حد ندفة ثلج كوخ هي m^1.26186,

تعاريف

لعل أكثر خواص الكسيريات إثارة هي لانظاميتها بشكل عام من حيث الشكل. ولهذا فهي ليست نمطاً من الأغراض القابلة للتعريف بالهندسة التقليدية، إن هذا يعني أن الكسيريات تنحو باتجاه إعطاء تفاصيل مرئية جديدة باستخدام المقاييس المختلفة، ففي حالة التشابه الذاتي، عند تكبير الكسيريات نحصل على صور مماثلة للأصل وغالباً ما تعرف مجموعات كهذه تعاودياً. إن أي شكل إقليدي كالدائرة على سبيل المثال، يبدو أكثر تسطحاً بزيادة التكبير، وعندما يصبح التكبير لانهائياً يصبح من المستحيل التمييز فيما إذا كان أصل الشكل دائرة أو خط مستقيم، تنعدم هذه الخاصة في الكسيريات. فالفكرة التقليدية للمنحني والتي تبين تغير نصف قطر الدائرة بالتقريب يصبح من المستحيل اعتمادها لغياب التقييس، في حين أن زيادة تكبير الكسيريات يظهر تفاصيل أكثر وأكثر كانت غائبة سابقاً. مثلما تظهر العديد من الصفات المميزة الخاصة بالكسيريات، يتعذر بشكل ملحوظ إجمالها في تعريف رياضي صريح ودقيق، لقد عرف ماندلبروت الفركتل على أنه "مجموعة يتجاوز فيها بعد هاوسندروف بعدها اللاكمي". فمن أجل شكل كسيري ذو تشابه ذاتي، فإن بعد هاسندروف يساوي إلى بعد مينكوفسكي بوليجاند.

من المشاكل التي تخص تعريف الكسيريات:

• لا يوجد تعريف دقيق لعبارة "شديد اللانظامية".
• لا يوجد تعريف دقيق للـ "بعد".
• توجد العديد من الطرق التي يمكن من خلالها تعريف كائنات ذات تشابه ذاتي.
• ليست كل الكسيريات معرفة بشكل تعاودي.

تقنيات مشهورة لتوليد الكسيريات

حتى لدى تكبير مجموعة ماندلبروت لألفي ضعف، تظهر تفاصيل جديدة تكون صوراً مشابهة للصورة الأصلية

يمكن تصنيف الكسيريات في ثلاث مجموعات رئيسية. تصنف هذه المجموعات الكسيريات اعتماداً على طرق توليدها أو تعريفها:

• أنظمة الدوال المتكررة — تحتوي هذه المجموعة على قاعدة استبدال هندسي واضحة لكل كسيرية. منها ندفة الثلج لكوخ ومجموعة كانتور وسجادة سربنسكي وحشية سربنسكي ومنحنى بيانو ومنحني التنين هارتر هايواي والمربع تي واسفنجة مينجر.
• كسيريات الانفلات الوقتي — تعرف الكسيريات في هذه المجموعة عبر علاقة تكرارية من أجل كل نقطة في الفراغ (كما في المستوى العقدي). أمثلة على ذلك مجموعة ماندلبروت ومجموعة جوليا وكسيرية الباخرة المحترقة وكسيرية نوفا وكسيرية ليابونوف.
• الكسيريات العشوائية تولد من خلال إجراءات مختارة بشكل عشوائي بدلاً من أن تكون محددة، أمثلة على ذلك المناظر الكسيرية ورحلة ليفي.
• الأنظمة اللامية,

يمكن تصنيف الكسيريات أيضاً اعتماداً على تشابهها الذاتي. توجد ثلاثة أنواع للتشابه الذاتي في الكسيريات:

• تشابه ذاتي متطابق — يعد أقوى أنواع التشابه الذاتي، تبدو الكسيريات ذاتها على أي مقياس تكبير، إن الكسيريات المعرفة باستخدام أنظمة التوابع التكرارية غالباً ما تكون ذات تشابه ذاتي متطابق.
• تشابه ذاتي ظاهري — وهو نمط غير محكم من التشابه الذاتي، تبدو الكسيريات متطابقة إلى حد ما (ولكن ليس تماماً) على مقاييس تكبير مختلفة، تحتوي كسيريات التشابه الذاتي الظاهري على نسخ مصغرة من كامل الفركتل ولكن بأشكال منحلة مشوهة، إن الكسيريات المعرفة بعلاقات تكرارية غالباً ما تكون ذات تشابه ذاتي ظاهري وليست ذات تشابه ظاهري متطابق.
• التشابه الذاتي الإحصائي — يعد من أضعف أنواع التشابه الذاتي، يبيدي الكسيرية قياسات رقمية أو إحصائية ثابتة على اختلاف مقاييس التكبير.

إن أكثر تعاريف الكسيريات بداهة تحتوي في مضمونها شكلاً من أشكال التماثل الظاهري الإحصائي، (البعد الكسيري أو الفركتلي مثلاً هو قياس رقمي محفوظ على اختلاف مقاييس التكبير). إن الكسيريات العشوائية هي أمثلة واضحة على كسيريات التشابه الذاتي الإحصائي، ولكنها ليست ذات تشابه ذاتي متطابق أو ظاهري. من الجدير بالملاحظة أنه ليست كل الأغراض ذات التماثل الذاتي هي فركتلات، فالخط الحقيقي (خط إقليدي متصل) مثلاً ذو تماثل ذاتي تام، إلا أن الادعاء بأن كامل الكائنات الإقليدية هي فركتلات يمثل موقف قلة من الأشخاص، فقد رأى ماندلبروت أن تعريف الكسيرية لا يجب أن يتضمن الكسيريات "الحقيقية" فقط، بل الأغراض الإقليدية الكلاسيكية، فوجود الأعداد الصماء على مستقيم الأعداد يولد خصائص معقدة لا متكررة. طالما أن البنية الحبيبية للكسيريات لا متناهية، فمن غير الممكن اعتبار أياً من الأغراض الطبيعية فركتلاً، على كل الأحوال، يمكن أن تبدي الأغراض الطبيعية خصائص مشابهة للفركتلات على عدد محدود من مقاييس التكبير.

أمثلة

مجموعة جوليا, هي كسيرية ترتبط إلى حد ما بمجموعة ماندلبروت

تتضمن الأمثلة الشائعة للكسيريات مجموعة ماندلبروت وكسيرية ليابونوف ومجموعة كانتور وحشية سربنسكي وسجادة سربنسكي واسفنجة مينجر ومنحني التنين ومنحني بيانو, والمجموعات المحدودة مجموعة كلاينايان, ومنحنى كوخ. قد تكون الكسيريات محددة أو مختارة بشكل عشوائي. الأنظمة الديناميكية الشواشية غالباً (إن ليس دائماً) تربط بالكسيريات. تتضمن مجموعة ماندلبروت أقراصاً كاملة ببعد يساوي 2، وهذا ليس مفاجئاً، ذلك أن الذي يفاجئ بشكل كبير هو أن بعد هاوسدروف لحد مجموعة ماندلبروت هو أيضاً 2.

مجموعة أخرى من الأمثلة المماثلة هي مجموعات كانتور، والتي بانتزاع فترات أصغر وأصغر من الفترة [0.1]، تترك مجموعات من الممكن (وقد يكون من غير الممكن) أن تحتوي على بنية تماثل ذاتي لدي تكبيرها، وقد تحتوي (أو لا تحتوي) على بعد d يقع بين 0 و 1. كتطبيق بسيط يظهر الترابط بين المفهومين، انتزاع الرقم 7 من الامتدادات العشرية يتصف بالتشابه الذاتي لدى تكبير انطوائي بمقدار العشرة، ولديه أيضاً البعد log9/log10 (تبقى القيمة ذاتها حتى لو قمنا بتغيير قاعدة اللوغاريتم)

• 

  فركتل متشكل جراء نزع ورقتين إكريليكيتين مطليتين بالغراء عن بعضهما

• 

  تفريغ فولطية عالية في بلوك إكريليكي يخلق فركتل شكل ليشتنبرغ.

• 

  فركتل متشكل جراء إضاءة دي في دي بأمواج ميكروية

• 

  رومانيسكو بروكولي يظهر فركتلات طبيعية رائعة

الكسيريات في الطبيعة

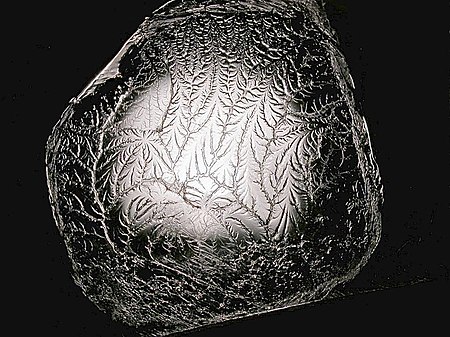
من الممكن مصادفة أشباه الكسيريات بكثرة في الطبيعة. تظهر كائنات كهذه بنية معقدة على امتداد تكبير منته. هذه الكسيريات التي تتولد طبيعياً (الغيوم والجبال وشبكات الأنهار وأنظمة الأوعية الدموية) لديها حدود دنيا وعليا، ولكنها تتميز عن بعضها بمقاييس تكبير مختلفة. على الرغم من وجود الكسيريات حولنا بكثرة، فإنها لم تدرس بشكل معمق حتى بدايات القرن العشرين، أما التعريفات العمومية لها فجاءت متأخرة قليلاً.

إن الأشجار والسراخس فركتلية بطبيعتها، ويمكن نمذجتها بالحاسب عبر استخدام خوارزميات تعاودية. تبدو الطبيعة العودية واضحة في هذه الأمثلة، ففرع الشجرة أو ورقة من السراخس هي تكرار مصغر للكل: ليس مطابقاً ولكنه مشابه من حيث الطبيعة.

برمجيات لتوليد الكسيريات

غالباً ما تولد الكسيريات باستخدام الحاسب. يوجد عدد كبير من البرامج التي تمكن من نمذجة الكسيريات كما يمكن لبعضها أن تقوم بتوليدها:

• Fractint (يعمل على مجموعة من منصات التشغيل)
• سترلينغ — برنامج توليد فركتلات محسن يخص أنظمة مايكروسوفت ويندوز من قبل ستيفن فيركسون.
• XaoS — برنامج سريع يعمل بالنظام الحقيقي يختص بنمذجة وتكبير الكسيريات (homepage).

التطبيقات في التكنولوجيا

يمكن وصف الهندسة الكسيرية بأنها النظام الحقيقى لكمية هائلة من الأنظمة الرياضية المعقدة في شكل تمثيلى قد تظهر من الوهلة الأولى أنها بلا نظامية إلا أنها الطريقة المثلى لتمثيل هذه البيانات. للكسيريات العشوائية تطبيقات هامة، ذلك أنه من الممكن استخدامها لوصف كائنات من العالم الحقيقي شديدة اللانظامية، أمثلة على ذلك الغيوم والجبال والاضطرابات والخطوط الساحلية والأشجار. تطبق التقنيات الكسيرية أيضاً في مجال ضغط الصور الفركتلي، بالإضافة إلى العديد من المجالات العلمية الأخرى.

هناك العديد من التطبيقات للكسيريات في الحقول التالية:

• تصنيف الشرائح التي تصف تغير مراحل الأمراض في الطب,
• ابتكار أنواع جديدة من الموسيقى,
• تخلق أشكال جديدة في مجال الفن,
• ضغط الصورة والإشارة,
• علم الزلازل,
• علم الكون,
• تصميم الألعاب الحاسوبية وخاصة فيما يتعلق بالصور الحاسوبية الخاصة بالبيئات العضوية.

مقالات ذات صلة

• تشعب (رياضيات)
• تأثير الفراشة
• نظرية الشواش
• تعقيد
• خوارزمية مربع الماس
• جريان مضطرب

المراجع

موسوعات ذات صلة :

• موسوعة رياضيات
• موسوعة هندسة رياضية