Levier (mécanique)

Levier utilisé pour retirer les planches d'un parquet.

En mécanique, un levier est une pièce rigide, allongée, généralement en liaison pivot ou en simple appui par rapport à une partie fixe, qui permet de transformer un mouvement^[1]. Le levier est l'une des huit machines simples.

Le levier peut être utilisé de deux manières :

pour amplifier un mouvement, en amplitude ou en vitesse ; l'une des premières applications fut sans doute l'atlatl ;
pour amplifier un effort.

Les deux utilisations sont contradictoires : l'amplification du mouvement se fait aux dépens de l'effort, et l'amplification de l'effort se fait aux dépens de la vitesse et de l'amplitude du mouvement.

Pour que le levier puisse jouer, il doit avoir un appui, appelé également hypomochlion ou hypomoclion (du grec ὑπο « sous » et μοχλός « levier »). C’est aussi l’axe sur lequel on peut faire levier pour tourner. Ce terme est utilisé, notamment en odonto-stomatologie, pour désigner le centre de rotation de la dent par rapport à son ancrage, au niveau du desmodonte.

Histoire

Si l’on entend par mécanisme la mise en place cohérente de plusieurs solides dans le but de transformer un mouvement, alors le levier est le plus simple de tous. Ce qui en fait probablement le premier mécanisme ou dispositif mécanique utilisé par l’Homme, bien avant la découverte de la roue. Il n’est formé que de deux solides : un appui (un caillou) et un levier (une branche, un bâton) qui disposés judicieusement permettent de démultiplier la force musculaire.

Il est mis en œuvre dans l'Antiquité, notamment sous forme de chadouf.

Bien plus tard, Archimède a compris et maîtrisé toutes les possibilités qu’offre le levier. Ce dispositif est d’ailleurs à l’origine de l'une de ses citations les plus célèbres^[2] : « Δός μοί ποῦ στῶ, καὶ κινῶ τὴν γῆν » (« Donne-moi où je puisse me tenir ferme, et j'ébranlerai la Terre »).

Classes de levier

Levier de première classe.

Levier de seconde classe.

Levier de troisième classe. Sur ce schéma, le levier fonctionne correctement si le point d'appui est attaché à la barre.

On regroupe traditionnellement les leviers en trois classes^[3], fonction de la position du point d'appui et des forces en entrée et sortie :

Première classe: levier inter-appui : le point d'appui est situé entre les deux forces, au milieu dans le cas d’un tape-cul. Exemples : le muscle triceps brachial du bras, un frein à main de vélo, un pied-de-biche (côté incurvé), un arrache-clou, une pince-tenaille, des ciseaux, un diable, un mors, un trébuchet, une balance.
Deuxième classe: levier inter-résistant : le point d'appui est à une extrémité du levier, la force exercée à l'autre, la force résultante se situe entre les deux. Exemples : une porte, un casse-noix, un tremplin de plongeon, une brouette, une clef, un décapsuleur, un pied-de-biche (côté droit), des pompes ou des rames (double leviers), un massicot à levier.
Troisième classe: levier inter-moteur : le point d'appui est à une extrémité du levier, la force résultante à l'autre, la force exercée se situe entre les deux. Exemples : le muscle biceps brachial, une batte de baseball, une fronde, une pagaie, un balai, une canne à pêche, une crosse de hockey, une pince à épiler et une pince à chiqueter, un coupe-ongles, un piège à souris, une pelle, une agrafeuse, une houe, une faux.

Le ratio des longueurs des bras de levier (entre chaque force et le point d'appui), et donc le ratio des forces et celui des déplacements, sont libres pour la première classe. Pour la seconde classe, la force résultante a un bras de levier forcément plus court : son déplacement sera moindre et la force exercée multipliée. Pour la troisième classe, c'est l'inverse : le bras de levier pour la force résultante étant forcément plus long, le déplacement le sera aussi, mais en contrepartie il faudra une force exercée plus forte.

Étude mécanique

Loi élémentaire des leviers

Dans une approche élémentaire, nous considérons deux efforts :

l'effort produit par l'actionneur — la personne manipulant le levier
l'effort produit par l'effecteur — la partie du levier qui fait le travail voulu.

Cette étude est peu rigoureuse, puisqu'elle ne passe pas par la démarche de la statique du solide (isolement du solide, bilan des actions mécaniques extérieures, application des principes de la statique), mais c'est cette étude qui a permis la découverte des principes fondant la statique.

Supposons également, pour simplifier, que le levier est droit (rectiligne) et que les efforts sont perpendiculaires au levier. On constate alors que le levier amplifie (ou réduit) l'effort proportionnellement au rapport des bras de levier, c'est-à-dire à la distance du pivot au point d'application de l'effort.

Isolement du levier

Dans une étude rigoureuse, il faut isoler le levier.

La liaison entre le levier et son appui est généralement unilatérale (un seul sens d’application d’effort est alors possible) dans le cas d'un levier amovible, ou constitue une articulation (pivot, rotule…).

Cet appui ne se situe pas obligatoirement entre les deux points d’application des forces, il peut être extérieur à ces points. C’est le cas par exemple pour la brouette.

D'autre part, le levier subit une charge, ce qu'on veut soulever ou pousser, et une force motrice, celle qu'on exerce en la souhaitant la plus faible possible.

L'équilibre sous trois forces — relation entre trois vecteurs — implique que le levier agit dans un plan. Il est possible que ce plan ne soit pas fixe, et tourne dans l'espace. C’est le cas d’un levier de vitesses automobile, maintenu par une liaison rotule à doigt.

L'étude qui suit présente un levier dans le plan cinématique et statique. Tous les vecteurs sont vus en vraie grandeur. Le levier est maintenu par un appui ponctuel ou linéaire rectiligne.

Étude cinématique

Déplacement d'un levier autour de son appui.

Les vecteurs ${\vec {V_{1}}}$ et ${\vec {V_{2}}}$ ont même angulation mais sont de sens opposés : ${\vec {V_{1}}}\cdot {\vec {V_{2}}}<0$ . Ces deux vecteurs peuvent représenter un déplacement (m), une vitesse (m/s) ou une accélération (m/s²).

Le théorème de Thalès nous donne la relation : ${\frac {\|{\vec {V_{1}}}\|}{\|{\vec {V_{2}}}\|}}={\frac {V_{1}}{V_{2}}}={\frac {L_{1}}{L_{2}}}$ .

Cette relation peut s'écrire plus utilement $V_{1}={\frac {L_{1}}{L_{2}}}\times V_{2}$ ou $V_{2}={\frac {L_{2}}{L_{1}}}\times V_{1}$ .

Un levier permet donc de transformer un déplacement, une vitesse ou une accélération selon le rapport de ses bras de levier.

Une utilisation guerrière de l'aspect cinématique du levier est le trébuchet. Dans ce cas, une masse attachée à une extrémité (L₁) est accélérée par la pesanteur terrestre, le levier augmente et transmet cette accélération à l'autre extrémité (L₂) afin de projeter un boulet.

Dans ce cas, outre l'amplification de la vitesse, on a également une multiplication de l'amplitude du mouvement, ainsi que de la force requise (dans le cas du trébuchet, le poids d'entrainement plusieurs fois supérieure à celui du boulet).

En sens inverse, on peut diviser la force requise pour exercer une force donnée, au prix de la division de l'amplitude de mouvement dans le même ratio.

Ceci est largement utilisé par les appareils de manutention, par exemple dans les chèvres hydrauliques, les tables à ciseaux, les plateformes et nacelles élévatrices, les échelles aériennes, les élévateurs de manège, …

Étude statique

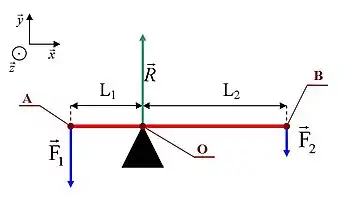
Levier en équilibre sous des actions extérieures.

Le principe fondamental de la statique (PFS) appliqué au système {levier} au point O donne deux équations vectorielles :

Pour les résultantes :

{\vec {\mathrm {F} _{1}}}+{\vec {\mathrm {F} _{2}}}+{\vec {\mathrm {R} }}={\vec {0}}

Soit, en projection sur ${\vec {y}}$ :

-\mathrm {F} _{1}-\mathrm {F} _{2}+\mathrm {R} =0\,

(1)

Pour les moments :

{\mathcal {M}}_{o}({\vec {\mathrm {F} _{1}}})+{\mathcal {M}}_{o}({\vec {\mathrm {F} _{2}}})+{\mathcal {M}}_{o}({\vec {\mathrm {R} }})={\vec {0}}

\Leftrightarrow {\vec {\mathrm {F} _{1}}}\wedge {\vec {\mathrm {AO} }}+{\vec {\mathrm {F} _{2}}}\wedge {\vec {\mathrm {BO} }}+{\vec {0}}={\vec {0}}

\Leftrightarrow -\mathrm {F} _{1}\cdot {\vec {y}}\wedge \mathrm {L} _{1}\cdot {\vec {x}}-\mathrm {F} _{2}\cdot {\vec {y}}\wedge (-\mathrm {L} _{2}{\vec {x}})={\vec {0}}

\Leftrightarrow \mathrm {F} _{1}\cdot \mathrm {L} _{1}\cdot {\vec {z}}-\mathrm {F} _{2}\cdot \mathrm {L} _{2}{\vec {z}}={\vec {0}}\,

Ce qui donne finalement en projection sur ${\vec {z}}$ :

\mathrm {F} _{1}\cdot \mathrm {L} _{1}-\mathrm {F} _{2}\cdot \mathrm {L} _{2}=0\,

que l'on écrira plus utilement :

\mathrm {F} _{1}\cdot \mathrm {L} _{1}=\mathrm {F} _{2}\cdot \mathrm {L} _{2}

{\frac {\mathrm {F} _{1}}{\mathrm {F} _{2}}}={\frac {\mathrm {L} _{2}}{\mathrm {L} _{1}}}

Remarques sur les résultats :

le rapport des bras de levier est inversé par rapport à la relation sur les vitesses ;
l'équation (1) permet de calculer l'effort que l'appui subit.

Le rapport des forces est donc inversement proportionnel au rapport des bras de levier.

Principe du levier sur la brouette :

\mathrm {P} \cdot a=\mathrm {F} \cdot b

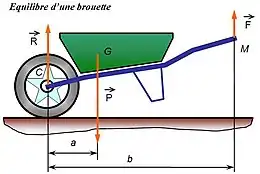
Le sécateur et le pied-de-biche, aussi appelé pince monseigneur, utilisent l'aspect statique du levier. Un petit effort appliqué par l'utilisateur sur le grand bras de levier permet d'obtenir un effort très important au niveau du petit bras de levier et permet ainsi de couper une branche ou d'arracher un clou.

De même, l'intérêt de la brouette, dans le transport de charges, repose sur ce principe.

Aspect énergétique

Le levier respecte le principe de la conservation de l'énergie.

En A, la puissance appliquée est ${\mathcal {P}}_{\mathrm {A} }=\mathrm {F} _{1}\times \mathrm {V} _{1}$ .

La puissance transmise en B est ${\mathcal {P}}_{\mathrm {B} }=\mathrm {F} _{2}\times \mathrm {V} _{2}$ .

Or nous avons vu que $\mathrm {V} _{1}={\frac {\mathrm {L} _{1}}{\mathrm {L} _{2}}}\times \mathrm {V} _{2}$ et que $\mathrm {F} _{1}={\frac {\mathrm {L} _{2}}{\mathrm {L} _{1}}}\times \mathrm {F} _{2}$ .

On a donc ${\mathcal {P}}_{\mathrm {A} }=\mathrm {F} _{1}\times \mathrm {V} _{1}={\frac {\mathrm {L} _{2}}{\mathrm {L} _{1}}}\times {\frac {\mathrm {L} _{1}}{\mathrm {L} _{2}}}\times \mathrm {F} _{2}\times \mathrm {V} _{2}=\mathrm {F} _{2}\times \mathrm {V} _{2}={\mathcal {P}}_{B}$ .

Ainsi la puissance et l’énergie sont intégralement transmises du point A au point B.

En pratique, une petite partie de la puissance est dégradée sous forme de chaleur et/ou de vibrations sonores au niveau de la liaison avec l’appui. Pour en tenir compte, il faut connaître le rendement de cette liaison.

À partir du principe de conservation de l'énergie (ici sous la forme du travail des forces) on retrouve les propriétés du levier, notamment le fait que le rapport des forces aux extrémités est égal au rapport inverse des longueurs des bras.

Travaux virtuels

Selon le principe des travaux virtuels, les déplacements de la structure sont si petits que sa géométrie n'est pas changée. Les grandeurs infinitésimales sont précédées du signe $d$ et nous plaçons le point 1 en A et 2 en B.

En 1, le travail virtuel vaut $d{\mathcal {W}}_{1}=\mathrm {F} _{1}\times dx_{2}$ .

Le travail virtuel en 2 est $d{\mathcal {W}}_{2}=\mathrm {F} _{2}\times dx_{1}$ .

Comme la structure ne travaille pas au repos, nous pouvons égaler ces deux travaux virtuels, donc $\mathrm {F} _{1}\times dx_{1}=\mathrm {F} _{2}\times dx_{2}$ .

Or les déplacements des points 1 et 2 sont liés par la géométrie de la structure car si nous considérons que les poutres restent parfaitement rigides, dès lors, $\mathrm {L} _{1}\times dx_{1}=\mathrm {L} _{2}\times dx_{2}$ .

On a donc $\mathrm {L} _{1}\times \mathrm {F} _{1}=\mathrm {F} _{2}\times \mathrm {L} _{2}$ .

Notes et références

↑ Informations lexicographiques et étymologiques de « Levier » (sens A) dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales
↑ Cité par Pappus d'Alexandrie, Collection mathématique,livre VIII, Chapitre XI (https://www.persee.fr/doc/antiq_0770-2817_1955_num_24_1_3257)
↑ « Test de raisonnement mécanique », sur Les tests psychotechniques en ligne expliqués (consulté le 10 juin 2019)

Voir aussi

Liens externes

Notices dans des dictionnaires ou encyclopédies généralistes :
Notices d'autorité :
- BnF (données)
- LCCN
- Israël