Pareto
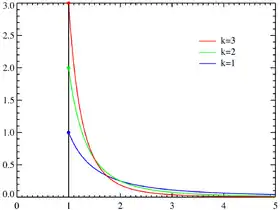Densité de probabilité Fonctions de masse pour plusieurs k avec xm = 1. L'axe horizontal symbolise le paramètre x . Lorsque k→∞ la loi s'approche de δ(x − xm) où δ est la « fonction » delta de Dirac.
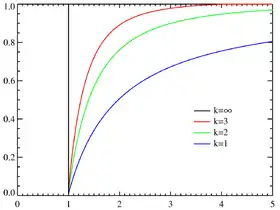Fonction de répartition Fonctions de répartition pour plusieurs k avec xm = 1. L'axe horizontal symbolise le paramètre x'
Paramètres	${\displaystyle x_{\mathrm {m} }>0}$ location (réel) ${\displaystyle k>0}$ forme (réel)
Support	${\displaystyle x\in [x_{\mathrm {m} };+\infty )\!}$
Densité de probabilité	${\displaystyle {\frac {k\,x_{\mathrm {m} }^{k}}{x^{k+1}}}\!}$
Fonction de répartition	${\displaystyle 1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{k}\!}$
Espérance	${\displaystyle {\frac {k\,x_{\mathrm {m} }}{k-1}}\!}$ pour ${\displaystyle k>1}$
Médiane	${\displaystyle x_{\mathrm {m} }{\sqrt[{k}]{2}}}$
Mode	${\displaystyle x_{\mathrm {m} }}$
Variance	${\displaystyle {\frac {x_{\mathrm {m} }^{2}k}{(k-1)^{2}(k-2)}}\!}$ pour ${\displaystyle k>2}$
Asymétrie	${\displaystyle {\frac {2(1+k)}{k-3}}\,{\sqrt {\frac {k-2}{k}}}\!}$ pour ${\displaystyle k>3}$
Kurtosis normalisé	${\displaystyle {\frac {6(k^{3}+k^{2}-6k-2)}{k(k-3)(k-4)}}\!}$ pour ${\displaystyle k>4}$
Entropie	${\displaystyle \ln \left({\frac {k}{x_{\mathrm {m} }}}\right)-{\frac {1}{k}}-1\!}$
Fonction génératrice des moments	non définie pour les réels strictement positifs
Fonction caractéristique	${\displaystyle k(-{\rm {i}}x_{\mathrm {m} }t)^{k}\Gamma (-k,-{\rm {i}}x_{\mathrm {m} }t)}$ où Γ désigne la fonction gamma incomplète

En théorie des probabilités, la loi de Pareto, d'après Vilfredo Pareto, est un type particulier de loi de puissance qui a des applications en sciences physiques et sociales. Elle permet notamment de donner une base théorique au « principe des 80-20 », aussi appelé principe de Pareto.

Définition

Soit la variable aléatoire X qui suit une loi de Pareto de paramètres (x_m,k), avec k un réel positif, alors la loi est caractérisée par :

${\displaystyle \mathbb {P} (X>x)=\left({\frac {x_{\mathrm {m} }}{x}}\right)^{k}\quad {\textrm {avec}}\quad x\geq x_{\mathrm {m} }}$

Densité de probabilité

Les lois de Pareto sont des lois continues. La loi de Zipf, et son cas limite, la loi zêta, peuvent être considérées comme l'équivalent discret de la loi de Pareto.

Il suit, de la définition donnée précédemment, que la densité de probabilité de X vérifie : ${\displaystyle f(x;k,x_{\mathrm {m} })=k\,{\frac {x_{\mathrm {m} }^{k}}{x^{k+1}}}}$ pour ${\displaystyle x\geq x_{\mathrm {m} }.}$

Le paramètre k est souvent nommé indice de Pareto.

Quantiles

Le quantile d'ordre ${\displaystyle \alpha }$ d'une variable aléatoire distribuée selon une loi de Pareto de paramètres ${\displaystyle \left(x_{m},k\right)}$ est donné par :

${\displaystyle q\left(\alpha \right)=x_{m}\left(1-\alpha \right)^{-{\frac {1}{k}}}}$

Moments

L'espérance d'une variable aléatoire suivant une loi de Pareto est

${\displaystyle \mathbb {E} (X)={\frac {kx_{\mathrm {m} }}{k-1}}\,}$

(si k ≤ 1, l'espérance est infinie).

Sa variance est

${\displaystyle \mathrm {Var} (X)=\left({\frac {x_{\mathrm {m} }}{k-1}}\right)^{2}{\frac {k}{k-2}}}$

(De nouveau : si k ≤ 2, la variance est infinie).

Les moments d'ordre supérieur sont donnés par :

${\displaystyle \mu _{n}'={\frac {kx_{\mathrm {m} }^{n}}{k-n}}\,}$

mais ils ne sont définis que pour ${\displaystyle k>n}$.

Cela signifie que la fonction génératrice (la série de Taylor en x où les ${\displaystyle \mu _{n}'/n!}$ sont pris pour coefficients) n'est pas définie. Cette propriété est vraie en général pour les variables aléatoires présentant une « longue traîne ».

La fonction caractéristique est donnée par :

${\displaystyle \varphi (t;k,x_{\mathrm {m} })=k(-ix_{\mathrm {m} }t)^{k}\Gamma (-k,-ix_{\mathrm {m} }t)}$

où Γ(a,x) est la fonction gamma incomplète .

La loi de Pareto est reliée à la loi exponentielle par :

${\displaystyle f(x;k,x_{\mathrm {m} })={\mathcal {E}}\left(\ln \left({\frac {x}{x_{\mathrm {m} }}}\right);k\right)\,}$

La loi de Dirac est un cas limite de la loi de Pareto :

${\displaystyle \lim _{k\rightarrow \infty }f(x;k,x_{\mathrm {m} })=\delta (x-x_{\mathrm {m} }).}$

Propriétés

La loi de Pareto est à longue traîne, ce qui signifie que :

${\displaystyle \forall y>0}$,${\displaystyle \lim _{x\rightarrow \infty }\mathbb {P} (X>x+y|X>x)=1}$ .

Par exemple, si X est le temps de vie d'un composant, plus il a vécu (X > x) plus il a de chances de vivre longtemps : le système rajeunit.

On peut pallier l'inconvénient « longue traîne » dans d'autres applications des lois de Pareto telles que la loi par taille des entreprises exprimée en nombre d'employés ou en chiffre d'affaires ou d'autres entités mesurables par taille dont la limite théorique est infinie en utilisant une échelle log-log après transformations appropriées des données analysées. Le phénomène longue traîne est causé par une variable pouvant atteindre des valeurs très grandes, valeurs pour lesquelles le nombre d'observations devient très petit ; en revanche le nombre d'observations pour les petites valeurs de la taille analysée sont souvent très élevées. Dans ce cas, on a le phénomène symétrique de la longue traîne : le long pic initial. Dans le cas de lois de Pareto, le passage en coordonnées log-log transforme en ligne droite la courbe dont la forme originale est une hyperbole très étirée en abscisse (longue traîne ou long-tailed) et ordonnée (hautes valeurs à la base)...

Applications

Cette loi est un outil fondamental en gestion de la qualité. Dans ce domaine elle permet de :

• hiérarchiser les problèmes en fonction du nombre d'occurrences (nombre d'apparitions) ;
• définir des priorités dans le traitement des problèmes.

Cet outil met en évidence la loi des 80/20. Autrement dit, agir sur 20 % de causes permet de résoudre 80 % du problème. Le pareto est utile pour identifier sur quelle cause agir en priorité pour améliorer de façon significative la situation.

Elle est aussi utilisée en réassurance. La théorie des files d'attente s'est intéressée à cette loi, lorsque des recherches des années 1990 ont montré que cette loi régissait aussi nombre de grandeurs observées dans le trafic Internet (et plus généralement sur tous les réseaux de données à grande vitesse). Ce phénomène a de sévères répercussions sur les performances des systèmes (routeurs en particulier).

Cette loi permet aussi d'analyser les phénomènes de concentration des entreprises industrielles et commerciales en fonction de leur taille exprimée en nombres d'employés. Une des représentations graphiques habituelles est obtenue en utilisant une double échelle logarithmique (log-log), représentation qu'avait lui-même utilisée Vilfredo Pareto. Dans ce cas la courbe se transforme en une ligne droite au-delà d'une certaine taille (tout comme pour la distribution des revenus des ménages qu'avait étudiée Pareto).

Autres domaines d'application : la distribution des ordinateurs en fonction de diverses mesures de leur taille (taille de la mémoire centrale, taille de la mémoire du disque dur), distribution des centraux téléphoniques privés en fonction du nombre de postes connectés.

Notes et références

Voir aussi