Méthode de Monte-Carlo

Une méthode de Monte-Carlo, ou méthode Monte-Carlo, est une méthode algorithmique visant à calculer une valeur numérique approchée en utilisant des procédés aléatoires, c'est-à-dire des techniques probabilistes.

Les méthodes de Monte-Carlo sont particulièrement utilisées pour calculer des intégrales en dimensions plus grandes que 1 (en particulier, pour calculer des surfaces et des volumes). Elles sont également couramment utilisées en physique des particules, où des simulations probabilistes permettent d'estimer la forme d'un signal ou la sensibilité d'un détecteur. La comparaison des données mesurées à ces simulations peut permettre de mettre en évidence des caractéristiques inattendues, par exemple de nouvelles particules.

La méthode de simulation de Monte-Carlo permet aussi d'introduire une approche statistique du risque dans une décision financière. Elle consiste à isoler des variables clés du projet, telles que le chiffre d'affaires ou la marge, et à leur affecter une loi de probabilités. Pour chacun de ces facteurs, un grand nombre de tirages aléatoires, suivant les lois de probabilité déterminées précédemment, est effectué, afin de trouver la probabilité d'occurrence de chacun des résultats. À titre d'exemple, le choix de mode de gestion d'une collectivité territoriale dans le cadre d'un partenariat public-privé (PPP) peut s'analyser par la méthode de Monte-Carlo, afin de prendre en compte la répartition des risques entre acteurs publics et privés. On parle alors de « risques valorisés » ou « valeurs à risque ».

Le véritable développement des méthodes de Monte-Carlo s'est effectué sous l'impulsion de John von Neumann et Stanislaw Ulam notamment, lors de la Seconde Guerre mondiale, et des recherches sur la fabrication de la bombe atomique. Ils ont en particulier utilisé ces méthodes probabilistes pour résoudre des équations aux dérivées partielles dans le cadre de la Monte-Carlo N-Particle transport (MCNP).

Le nom de ces méthodes, qui fait allusion aux jeux de hasard pratiqués au casino de Monte-Carlo, a été inventé en 1947 par Nicholas Metropolis^[1], et apparaît pour la première fois en 1949 dans un article coécrit avec Stanislaw Ulam^[2].

Théorie

De manière générale, le problème que l'on cherche à résoudre par les méthodes de Monte-Carlo est celui de l'estimation de l'espérance d'une variable aléatoire $X$ , que l'on note généralement $\mathbb {E} [X]$ .

La méthode de Monte-Carlo la plus simple consiste à générer un échantillon de variables aléatoires indépendantes et identiquement distribuées (iid) $X_{1},\dots ,X_{n}$ suivant la même loi que $X$ . Ensuite on estime l'espérance $\mathbb {E} [X]$ avec l'estimateur, dit de Monte-Carlo ou encore de la moyenne empirique,

\mu _{n}:={\frac {1}{n}}\sum _{k=1}^{n}X_{k}.

Ainsi $\mu _{n}$ est censé être une bonne approximation de la valeur que l'on recherche, à savoir $\mathbb {E} [X]$ . Cet estimateur est non biaisé dans le sens où $\mathbb {E} [\mu _{n}]=\mathbb {E} [X]$ . Ce qui justifie la pertinence de cet estimateur est la loi forte des grands nombres qui nous dit que, si $X$ admet une espérance finie (ce qui est en pratique très souvent le cas puisque l'on cherche justement à estimer cette espérance qui a priori est finie), alors on a la convergence presque sûre $\mu _{n}\rightarrow \mathbb {E} [X]$ lorsque la taille de l'échantillon $n$ tend vers l'infini.

Il est même possible de connaître l'ordre de grandeur de l'erreur commise par cet estimateur grâce au théorème central limite. En effet, si $X$ admet une variance finie $\sigma ^{2}<\infty$ , alors le théorème central limite nous dit que la convergence

{\frac {\mu _{n}-\mathbb {E} [X]}{\sigma }}\times {\sqrt {n}}\rightarrow {\mathcal {N}}(0,1)

a lieu en loi quand $n$ tend vers l'infini, où ${\mathcal {N}}(0,1)$ désigne une loi normale centrée réduite. On peut donc en déduire que, si $X$ admet une variance finie, alors l'erreur de l'estimateur de Monte-Carlo est de l'ordre de $1/{\sqrt {n}}$ et l'on voit bien que plus la taille de l'échantillon est grande, plus l'erreur se rapproche de zéro. Par exemple, multiplier par 100 la taille de l'échantillon devrait, à peu près, diviser par 10 l'erreur commise.

En utilisant le théorème central limite, on peut déduire des intervalles de confiance asymptotiques pour l'estimateur de Monte-Carlo. Soit un réel $\alpha \in [0,1]$ qui correspond au niveau de confiance désiré et notons $q_{\beta }$ le quantile d'ordre $\beta$ de la loi normale centrée réduite. C'est-à-dire que, si $Z\sim {\mathcal {N}}(0,1)$ alors $\mathbb {P} (Z\leq q_{\beta })=\beta$ (par exemple pour $\beta =97.5\%$ on a $q_{0,975}\approx 1,96$ ). Alors on a la convergence

\mathbb {P} \left(\mathbb {E} [X]\in \left[\mu _{n}-{\frac {\sigma q_{1-\alpha /2}}{\sqrt {n}}},\mu _{n}+{\frac {\sigma q_{1-\alpha /2}}{\sqrt {n}}}\right]\right)\rightarrow 1-\alpha

lorsque $n$ tend vers l'infini. Il faut garder en tête que cet intervalle de confiance est bien asymptotique et pas exact car se repose sur le théorème central limite qui est un résultat de convergence et non une égalité. En pratique, on connaît rarement la variance $\sigma ^{2}$ de $X$ ce qui est gênant dans le calcul de l'intervalle de confiance asymptotique ci-dessus. On peut résoudre ce problème en approximant cette variance via l'estimateur

\sigma _{n}^{2}:={\frac {1}{n}}\sum _{k=1}^{n}(X_{k}-\mu _{n})^{2}.

Encore une fois, par la loi forte des grands nombres, cet estimateur converge vers la variance $\sigma ^{2}$ lorsque cette dernière est finie.

Il est à noter que pour appliquer la méthode de Monte-Carlo décrite ci-dessus, il est supposé qu'il est possible de générer des variables aléatoires suivant la loi de $X$ . En pratique, cela peut constituer une difficulté à part entière, de plus il n'est pas toujours possible de générer facilement de telles variables aléatoires avec exactitude. Dans ce dernier cas, on cherchera alors à générer des variables aléatoires suivant une loi approximant au mieux la loi théorique de $X$ .

La méthode de Monte-Carlo présentée ci-dessus est l'une des versions les plus simples et épurées qui soient. Il existe de nombreuses variantes, plus précises ou plus rapides ou adaptées à d'autres circonstances, dont certaines sont mentionnées dans la section dédiées plus bas.

Applications

Estimer l'aire d'une surface ou un volume

Une grande catégorie de problèmes pouvant se résoudre par l'approche de Monte-Carlo est celle de l'estimation de l'aire d'une surface ou plus généralement d'un volume en dimension quelconque. Le principe général consiste à générer des points uniformément au hasard dans une zone bornée mais assez large pour contenir la surface ou le volume à estimer. Ensuite, il suffit de compter le nombre de points tombant dans la surface ou le volume et de diviser par le nombre total de points générés pour estimer l'aire ou le volume. Quelques exemples sont présentés ci-dessous.

Détermination de la superficie d'un lac

Cet exemple est un classique en vulgarisation de la méthode de Monte-Carlo. Soit une zone rectangulaire ou carrée dont les côtés sont de longueur connue. Au sein de cette aire se trouve un lac dont la superficie est inconnue. Grâce aux mesures des côtés de la zone, on connaît l'aire du rectangle. Pour trouver l'aire du lac, on demande à une armée de tirer $X$ coups de canon de manière aléatoire sur cette zone. On compte ensuite le nombre $N$ de boulets qui sont restés sur le terrain ; on peut ainsi déterminer le nombre de boulets qui sont tombés dans le lac : $X - N$ . Il suffit ensuite d'établir un rapport entre les valeurs :

{\frac {\mathrm {superficie} _{~\mathrm {terrain} }}{\mathrm {superficie} _{~\mathrm {lac} }}}={\frac {X}{X-N}}

\Longrightarrow \qquad \mathrm {superficie} _{~\mathrm {lac} }={\frac {(X-N)}{X}}\ \times \ \mathrm {superficie} _{~\mathrm {terrain} }

Par exemple, si le terrain fait 1 000 m², que l'armée tire 500 boulets et que 100 projectiles sont tombés dans le lac, alors une estimation de la superficie du plan d'eau est de : 1000×100÷500 = 200 m².

Estimation de la surface du lac grâce à des tirs d'artillerie aléatoires.

La qualité de l'estimation s'améliore (lentement) en augmentant le nombre de tirs et en s'assurant que les artilleurs ne visent pas toujours le même endroit mais couvrent bien la zone, de manière uniforme. Cette dernière remarque est à mettre en parallèle avec la qualité du générateur aléatoire qui est primordiale pour avoir de bons résultats dans la méthode de Monte-Carlo. Un générateur biaisé est comme un canon qui tire toujours au même endroit : les informations qu'il apporte sont réduites.

Détermination de la valeur de $π$

Cette méthode est proche de l'expérience de l'aiguille de Buffon.

Soit un point M de coordonnées $(x, y)$ , où $0 < x < 1$ et $0 < y < 1$ . On tire aléatoirement les valeurs de $x$ et $y$ entre 0 et 1 suivant une loi uniforme. Le point M appartient au disque de centre (0,0) de rayon $R = 1$ si et seulement si $x 2 + y 2 \leq 1$ . La probabilité que le point M appartienne au disque est $π / 4$ , puisque le quart de disque est de surface $σ= π R 2 / 4 = π / 4$ , et le carré qui le contient est de surface $S = R 2 =1$ : si la loi de probabilité du tirage de point est uniforme, la probabilité de tomber dans le quart de disque vaut $σ / S = π / 4$ .

En faisant le rapport du nombre de points dans le disque au nombre de tirages, on obtient une approximation du nombre $π / 4$ si le nombre de tirages est grand.

Représentation du calcul de la valeur de

π

par rapport du nombre de points aléatoires étant contenus dans un quart de cercle, l'ensemble des possibles étant un carré de côté R.

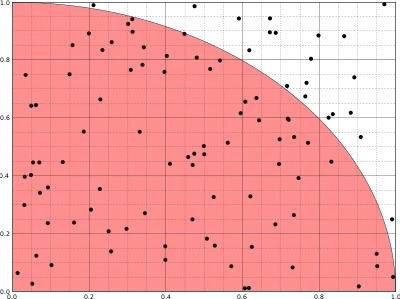
Calcul d'une intégrale

L'intégrale d'une fonction correspond à l'aire algébrique sous sa courbe. Estimer l'intégrale d'une fonction revient donc à estimer l'aire d'une surface et on peut donc appliquer une méthode de Monte-Carlo.

Par exemple supposons que l'on veuille estimer l'intégrale suivante

\int _{0}^{1}f(u)du

où $f:[0,1]\rightarrow \mathbb {R}$ est une fonction continue. Cette intégrale peut être vue comme une espérance. En effet, soit $U$ une variable aléatoire de loi uniforme sur $[0,1]$ , alors par la formule du transfert on a

\mathbb {E} [f(U)]=\int _{0}^{1}f(u)du.

On peut alors appliquer une méthode simple de Monte-Carlo et générer $n$ variables aléatoires iid $U_{1},\dots ,U_{n}$ uniformément au hasard dans $[0,1]$ et approximer l'intégrale ci-dessus par

{\frac {1}{n}}\sum _{k=1}^{n}f(U_{k}).

Ce procédé peut s'appliquer à une intégrale en dimension quelconque et pas nécessairement en dimension une comme ici. D'ailleurs en grande dimension, les méthodes de Monte-Carlo sont bien plus efficaces que d'autres méthodes classiques comme celle des sommes de Riemann par exemple.

Recouvrement de courbes et méthode contrainte-résistance

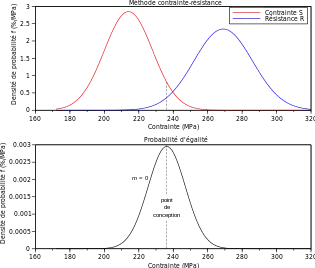
Méthode contrainte-résistance : la fréquence de défaillance correspond à l'aire sous l'intersection des courbes rouge et bleue (haut).

La méthode de Monte-Carlo peut être utilisée pour déterminer l'aire sous l'intersection de deux courbes, qui n'est qu'une surface particulière.

Les courbes peuvent être les courbes représentatrices des densités de probabilité de deux lois. C'est par exemple utilisé dans la méthode contrainte-résistance :

un système est soumis à une contrainte — une sollicitation quelle qu'elle soit (effort mécanique, variation de température, passage de courant électrique, …) — dont l'intensité est une variable aléatoire S ;
le système est conçu pour résister à cette contrainte, sa résistance est exprimée par une valeur, une variable aléatoire R ;
le système est validé si la résistance est supérieure à la contrainte — R > S — dans un certain nombre de cas (typiquement 99 % ou 99,9 %).

La probabilité complémentaire — les cas de défaillance, celle pour laquelle R ≤ S — est l'aire sous l'intersection des deux courbes représentant les lois.

On peut déterminer la probabilité P(R > S) en faisant des tirages aléatoires sur R et S et en dénombrant les cas pour lesquels « R > S » est vrai.

Application au modèle d'Ising

Estimation de la valeur d'un coup au go

Aux échecs, comme dans beaucoup de jeux de plateau, il est possible de mesurer la valeur d'une position, et donc des coups y conduisant, en évaluant quantitativement la position obtenue : nombre de pièces sur l'échiquier, valeurs des pièces (1 point par pion, 5 par tour...), position relative des pièces entre elles, et en pondérant la valeur trouvée par les libertés, les protections des pièces, etc. Cette évaluation basée sur l'analyse et l'expertise est d'autant plus rapide à mesurer qu'on avance dans la partie, car le nombre de pièces diminue.

Dans le jeu de go, l'évaluation d'une position globale reste très difficile avec des méthodes d'analyses classiques du fait de l’enchevêtrement et de la complexité des positions locales et du nombre quasi infini de suites de coups possibles. En 2006, le mathématicien Rémi Coulom a fait progresser de manière très sensible cette fonction d'évaluation et l’efficience des logiciels de jeu de go en utilisant la méthode de Monte-Carlo : on joue "au hasard" un grand nombre de fins de parties réalistes à partir de la position "en cours d'évaluation" et on comptabilise la proportion de parties gagnantes/perdantes. Cette estimation statistique s'affine en biaisant le hasard par élimination de coups a priori stupides. Cette méthode s'avère très efficace^[3]^,^[4]. Elle est utilisée en particulier par les programmes AlphaGo et AlphaZero^[5].

Estimation de la valeur d'un coup aux échecs

Parfois, pour savoir si un coup ambigu doit être fait (échange de pièces par exemple), lorsqu'on manque d'information , ou pour choisir entre plusieurs coups menant tous à des pertes de matériel, il est possible de lancer plusieurs parties rapides au hasard, pour savoir quelle est la moins mauvaise ou la meilleure des solutions.

Probabilité de la performance en bourse

Selon l'hypothèse des marchés efficients, les performances boursières sont aléatoires et suivent une loi normale. Dans ces conditions, il est possible de réaliser des milliers de tirages aléatoires pour déterminer les probabilités d'atteindre certaines performances boursières dans le futur^[6]. Cette caractéristique des marchés financiers permet d'utiliser la méthode de Monte-Carlo pour valoriser des options, ou encore des SPAC.

Espérance du gain d'une option dans le modèle de Black et Scholes

On note $S_{t}$ le prix d'un actif fixé au temps $t$ . Le modèle de Black et Scholes consiste à dire que le prix de cet actif répond à l'équation différentielle stochastique suivante : $dS_{t}=S_{t}(\mu dt+\sigma dW_{t})$ où $\mu$ est un réel (appelé parfois dérive), $\sigma$ est un réel positif (appelé volatilité) et $W$ désigne un mouvement brownien standard.

On suppose que l'on veuille estimer l'espérance du gain perçu par la détention d'une option européenne d'achat (call) de maturité $T$ et de prix d'exercice (strike) $K$ . Si le prix au temps $T$ , à savoir $S_{T}$ , est plus grand que $K$ , l'option est exercée et le gain est de $S_{T}-K$ , sinon le gain est nul. On cherche donc à estimer la quantité $\mathbb {E} [(S_{T}-K)_{+}]$ où $x_{+}:=\max(0,x)$ .

Pour estimer cette espérance, on peut avoir recours à une méthode de Monte-Carlo. Pour cela, il faut alors pouvoir générer des variables aléatoires suivant la loi de $S_{T}$ . On peut utiliser directement la forme de la solution de l'équation différentielle stochastique, à savoir

S_{t}=S_{0}\exp \left(\mu t-{\frac {\sigma ^{2}}{2}}t+\sigma W_{t}\right)\qquad \forall t\geq 0.

Il suffit alors de générer des variables aléatoires iid de même loi que $W_{T}$ qui est simplement une gaussienne centrée de variance $T$ . On approxime ensuite l'espérance du gain de l'option par

{\frac {1}{n}}\sum _{k=1}^{n}(S_{T}^{k}-K)_{+}

où $S_{T}^{1},\dots ,S_{T}^{n}$ sont $n$ variables iid de même loi que $S_{T}=S_{0}\exp(\mu t-\sigma ^{2}/2t+\sigma W_{T})$ .

Maintenant on suppose que l'on veuille étudier cette fois-ci une option américaine et non plus européenne. Dans ce cas il nous faudra générer tout le processus $(S_{t})_{t\leq T}$ et non plus simplement la variable $S_{T}$ . Une solution consiste à utiliser la méthode d'Euler à partir de l'équation différentielle stochastique. On commence par découper l'intervalle de temps $[0,T]$ en $M$ parties égales et on pose $\Delta t:=T/M$ . Ensuite on génère une suite de variables aléatoires

\left\{{\begin{array}{lll}S_{0}^{1}&=&S_{0}\\S_{(i+1)\Delta t}^{1}&=&S_{i\Delta t}^{1}(1+\mu \Delta t+\sigma Z_{i}^{1}{\sqrt {\Delta t}})\qquad \forall i<M\end{array}}\right.

où $Z_{0}^{1},\dots ,Z_{M-1}^{1}$ sont des gaussiennes centrées réduites indépendantes. On complète ensuite par interpolation linéaire. Pour $M$ choisi très grand, le processus aléatoire ainsi construit $(S_{t}^{1})_{t\leq T}$ devrait avoir une loi assez proche de celle de $(S_{t})_{t\leq T}$ . On peut répéter la construction précédente pour obtenir $n$ processus aléatoires $(S_{t}^{1})_{t\leq T},\dots ,(S_{t}^{n})_{t\leq T}$ iid de loi proche de celle de $(S_{t})_{t\leq T}$ .

Méthodes accélérées

Diverses méthodes, dites techniques de réduction de la variance, permettent d'améliorer la précision — ou de diminuer le temps de calcul — en remplaçant $X$ par une autre variable aléatoire. Ces techniques entrent en général dans l'une des classes suivantes : l'échantillonnage préférentiel, les variables de contrôle, la variable antithétique, la stratification et le conditionnement.

Le nombre de simulations $n$ nécessaires pour atteindre une marge d'erreur voulue est parfois trop important avec la méthode Monte-Carlo. Pour remédier à ce problème il existe des méthodes dites de « réduction de variance » ou de « Monte-Carlo accélérées » qui demandent moins de simulations pour atteindre le même niveau de précision. Parmi ces méthodes on distingue deux grands types de méthodes : les méthodes d'échantillonnage préférentiel et les méthodes particulaires.

Notes et références

↑ Nicholas Metropolis, « The Beginning of the Monte Carlo Method », Los Alamos Science, n^o 15,‎ 1987, p. 125-130 (lire en ligne).
↑ Nicholas Metropolis et Stanislaw Ulam, « The Monte Carlo Method », Journal of the American Statistical Association, vol. 44, n^o 247,‎ septembre 1949, p. 335-341 (DOI 10.2307/2280232, lire en ligne).
↑ « le jeu de go, le seul jeu où l'ordinateur ne bat pas l'homme », sur Slate, 5 mai 2014 (consulté le 15 septembre 2015).
↑ « le jeu de go et la révolution de monte-carlo », sur https://interstices.info, 28 mai 2009 (consulté le 15 septembre 2015).
↑ (en) David Silver et Demis Hassabis, « AlphaGo: Mastering the ancient game of Go with Machine Learning », sur Google Research Blog, 27 janvier 2016.
↑ Edouard Petit, « Prévoir la bourse et votre patrimoine grâce aux simulations de Monte-Carlo », sur Epargnant 3.0, 8 avril 2018 (consulté le 16 janvier 2020).

Voir aussi

Bibliographie

Emmanuel Gobet, Méthodes de Monte-Carlo et processus stochastiques - du linéaire au non linéaire, Éditions de l'École polytechnique, 2013
Carl Graham, Denis Talay, Simulation stochastique et méthodes de Monte-Carlo, Éditions de l'École polytechnique, 2011
(en) Introduction to Monte Carlo Algorithm Werner Krauth - CNRS, Laboratoire de Physique Statistique, École Normale Supérieure
(en) Michael Mascagni, Advanced Monte Carlo Methods I & II, Cours du ETH de Zurich (2005/2006). [PDF] Notes de cours. On pourra également consulter la page de présentation du cours, qui contient de nombreuses références disponibles au format en pdf.
Simon Léger, Monte Carlo pour les nuls, 2006 [PDF] [lire en ligne]
Une explication de la méthode de Monte-Carlo par le physicien Pierre Auger
J. Morio et M. Balesdent, Estimation of Rare Event Probabilities in Complex Aerospace and Other Systems : A Practical Approach, Cambridge, Elsevier Science, 2015, 216 p. (ISBN 978-0-08-100091-5)
(en) Cours de problèmes inverses par méthode de Monte Carlo - A. Tarantola, Institut de Physique du Globe de Paris
(en) Christian Robert et George Casella, Monte Carlo Statistical Methods, Springer-Verlag, coll. « Springer Texts in Statistics », 2010
(en) Christian Robert (statisticien) et George Casella, Introducing Monte Carlo Methods with R, Springer-Verlag, coll. « Use R! Series », 2007, 283 p. (ISBN 978-1-4419-1575-7, lire en ligne)

Liens externes

(en) Un exemple de simulation Monte-Carlo clair et didactique L'exemple se base sur la fabrication d'une pièce mécanique à partir de ses composants.
(en) MATLAB Monte-Carlo simulator with several examples