يشكل تاريخ ميكانيكا الكم جزأ أساسي من تاريخ الفيزياء الحديثة. غير أنه يتقاطع مع تاريخ كيمياء الكم أيضًا؛ بدأ تاريخ ميكانيكا الكم بعدد من الاكتشافات العلمية: منذ اكتشف مايكل فارادي آشعة الكاثود عام 1838 مٍ، وفسر جوستاف كيرشوف نظرية إشعاع الجسم الأسود شتاء 1859 – 1860مٍ، كما قام بولتزمان بافتراض أن كل مستوى طاقة لجسم فيزيائي ما يكون مُحدَّد وغير متصل (كمِّي) ، اكتشف أيضًا هيرتز ظاهرة التأثير الكهروضوئي عام 1887مٍ، وفي عام 1900 مٍ قدَّم ماكس بلانك نظرية يصف فيها الضوء وأي نظام ذري مُشَع للطاقة بأن له القدرة نظريًا على إشعاع عدد من وحدات الطاقة المحددة قيمتها إيبسلون "ε" كل وحدة تتناسب طرديًا مع تردد الإشعاع تبعًا للمعادلة الآتية:
حيث h هي قيمة عددية ثابتة سمَّاها ثابت بلانك.
ثم أستطاع أينشتين عام 1905 مٍ أن يفسر ظاهرة التأثير الكهروضوئي التي لاحظها وسجلها عمليًا هاينريش هيرتز عام 1887 مٍ كما ذكرنا، تزامن ذلك مع افتراض ماكس بلانك مما أكد الطبيعة الكمية للضوء؛ باعتبار الضوء شكل من أشكال الطاقة الإشعاعية يتكون من تيار من الجسيمات (كمَّات من الطاقة)، كل جسيم يشكِّل جزأ من طاقة محددة ومنفصلة، سمَّى جيلبرت لويس هذه الجسيمات بالفوتونات عام 1926. لوحظ التأثير الكهروضوئي عمليًا عند تعريض سطح مادة –معدن ما- لضوء له أطوال موجيّة مُعيّنه، يؤدَّى ذلك لانبعاث بعض إلكترونات إذا كان مجموع طاقة الضوء أكبر من دالة الشغل لسطح هذا المعدن.
في أوائل عشرينات القرن العشرين صيغت عبارة "ميكانيكا الكم" لأول مرة (بالألمانية، Quantenmechanik) ، على يد مجموعة من الفيزيائيين تتضمن ماكس بورن وهايزنبرج وفولفغانغ باولي بجامعة غوتينغن ، واستُخدم بحثيًا لأول مرة في رسالة لبورن بعنوان "Zur Quantenmechanik"[1] عام 1924مٍ. فيما بعد بدأ تطبيق هذه النظريات لتتوقع التركيب الكيميائي والتفاعلية والترابط الكيميائي للعناصر.
نظرة عامة
اقترح لودفينغ بولتزمان عام 1877 مٍ أن مستويات الطاقة لأي نظام مادي -كالجزيء مثلًا- يمكن أن تكون منفصلة. أسس بولتزمان نادي الرياضيات النمساوي، جنبا إلى جنب مع الرياضيين جوستاف فون إيشيرش و اميل مولر. برهن بولتزمان وجود مستويات طاقة منفصلة في الجزيئات ضاربًا بجزيء غاز اليود مثالًا (معروف أن جزيئات عنصر اليود تتحلّل في درجات حرارة عالية إلى ذرات)، ولتوضيح ذلك رسم بولتزمان احدى أولى الرسومات التوضيحية التي توضح تداخلات مدارات الذرات، مستندًا بذلك ببعض حسابات الميكانيكا الإحصائية، وكانت نظرياته أيضًا مدعومة بالحجج الرياضية ، كما سيتأكد ذلك بعد عشرين عاما مع أول ظهور أول نظرية للكم يطرحها ماكس بلانك.
في عام 1900 ، الفيزيائي الألماني ماكس بلانك افترض على مضض فكرة الطبيعة الكميّة للطاقة ليستنتج معادلة رياضية توضح اعتماد التردد الاشعاعي على الطاقة المنبعثة من الجسم الأسود -يتغيّر لون الحديد المتوّهج من الأحمر إلى الأبيض عند تسخينه- سُميّت بقانون بلانك، والذي أدَّى لاستنتاج توزيع بولتزمان القابل للتطبيق في مجال الفيزياء الكلاسيكية. يمكننا صياغة قانون بلانك[2] على النحو التالي: حيث:
- I(ν,T) الطاقة الصادرة من 1 سم مربع من سطح الجسم الأسود، لكل ثانية، في وحدة الزاوية الصلبة، عندما يصدر إشعاع تردده 1 هيرتز، عند درجة حرارة T؛
- h ثابت بلانك؛
- c سرعة الضوء في الفراغ؛
- k ثابت بولتزمان؛
- ν (نيو) تردد الإشعاع الكهرومغناطيسي ؛
- T هي درجة حرارة الجسم بمقياس كلفن.
وعلاوة على ذلك، فإن تطبيق بلانك نظرية الكم أن الإلكترون يسمح Ștefan Procopiu في 1911-1913 ثم نيلز بور عام 1913 ، لحساب العزم المغناطيسي للإلكترون الذي كان يسمى في وقت لاحق "magneton"؛مماثلة الكم الحسابات، ولكن مع عدديا مختلفة تماما القيم بعد ذلك جعلت من الممكن لكل المغناطيسي لحظات من البروتون و النيوترون التي هي ثلاثة أوامر من حجم أصغر من الإلكترون.
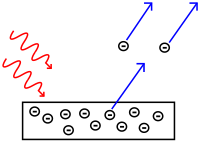
| Photoelectric effect | |
 The emission of electrons from a metal plate caused by light quanta (photons) with energy greater than the work function of the metal. | |
| The photoelectric effect reported by Heinrich Hertz in 1887, | |
| and explained by Albert Einstein in 1905. | |
| Low-energy phenomena: Photoelectric effect | |
| Mid-energy phenomena: Compton scattering | |
| High-energy phenomena: Pair production | |
في عام 1923 ، الفيزيائي الفرنسي لويس دي بروجلي طرح نظريته من موجات المسألة بالقول أن الجسيمات يمكن أن تحمل خصائص الموجة والعكس بالعكس. وكانت هذه النظرية على جسيم واحد والمستمدة من النظرية النسبية الخاصة. بناء على دي بروجلي نهج الحديثة ميكانيكا الكم ولد في عام 1925، عندما الفيزيائيين الألمان فيرنر هايزنبرغ، ماكس بورن، باسكوال جوردان[3][4] وضعت مصفوفة الميكانيكا والفيزيائي النمساوي إرفين شرودنغر اخترع موجة ميكانيكا وغير النسبية في معادلة شرودنغر كما تقريبي إلى عمم حالة دي بروجلي نظرية.[5] شرودنغر في وقت لاحق تبين أن هذين النهجين ما يعادلها.
مقالات ذات صلة
المراجع
- Max Born, My Life: Recollections of a Nobel Laureate, Taylor & Francis, London, 1978. ("We became more and more convinced that a radical change of the foundations of physics was necessary, i.e., a new kind of mechanics for which we used the term quantum mechanics. This word appears for the first time in physical literature in a paper of mine...")
- M. Planck (1914). The theory of heat radiation, second edition, translated by M. Masius, Blakiston's Son & Co, Philadelphia, pp. 22, 26, 42–43.
- David Edwards,The Mathematical Foundations of Quantum Mechanics, Synthese, Volume 42, Number 1/September, 1979, pp. 1–70.
- D. Edwards, The Mathematical Foundations of Quantum Field Theory: Fermions, Gauge Fields, and Super-symmetry, Part I: Lattice Field Theories, International J. of Theor. Phys., Vol. 20, No. 7 (1981).
- Hanle, P.A. (December 1977), "Erwin Schrodinger's Reaction to Louis de Broglie's Thesis on the Quantum Theory.", Isis, 68, صفحات 606–09, doi:10.1086/351880