حمل متحرك

في ديناميكا المنشأت, الحمل المتحرك هو الحمل الذي يتغير في مكان تأثيره مع مرور الزمن .أمثلة: العربات التي تمر علي الكباري, قطارات علي سكة الحديد ,.......وهكذا. في النماذج الحاسويبة ,يتم تطبيق الحمل على شكل:

اهتزاز عرضاني لغشاء (vibration lateral to a membrane)

هزاز توافقي رأسي.

• قوة بسيطة ليس لها وزن.
• مذبذب.
• قوة القصور الذاتي.

توجد العديد من المراجعات التاريخية المهتمه بالأحمال المتحركة (أمثلة^[1][2]) . والكثير من المنشورات العلمية تهتم بمسائل مشابهه^[3] .

بانتوغراف

قطار

بندقية

أمثلة لحمل متحرك.

قوة

مذبذب

كتلة

أمثلة لأحمال متحركة.

الدراسة الأصلية كانت متعلقة بحمل غير مصحوب بكتلة^[4]، وبعد ذلك تم وصف قوي القصور الذاتي في النماذج الرياضية^[5] بخصائص غير متوقعة للمعادلات التفاضلية التي تحكم حركة جسيم ذو كتلة يتحرك علي زنبرك، مثل كمرة توموشينكو وسطح ميندلين ^[6].

نفرض وتر مرتكز ارتكاز بسيط علي طرفيه له طول l ومساحة مقطع A وكثافة ρ ومشدود بقوة N يتعرض لفوة ثابتة P تتحرك بسرعة ثابتة v فإن معادلة الحركة لهذا الوتر تحت تأثير الحمل المتحرك لها الصيغة :

${\displaystyle -N{\frac {\partial ^{2}w(x,t)}{\partial x^{2}}}+\rho A{\frac {\partial ^{2}w(x,t)}{\partial t^{2}}}=\delta (x-vt)P\ .}$

التشكل الحادث لأي نقطة علي الوتر تعطي بالمتسلسلة

${\displaystyle w(x,t)={\frac {2P}{\rho Al}}\sum _{j=1}^{\infty }{\frac {1}{\omega _{(j)}^{2}-\omega ^{2}}}\left(\sin(\omega t)-{\frac {\omega }{\omega _{(j)}}}\sin(\omega _{(j)}t)\right)\ }$

حيث

${\displaystyle \omega ={\frac {j\pi v}{l}}\ }$

والاهتزاز الطبيعي الدائري للوتر

${\displaystyle \omega _{(j)}^{2}={\frac {j^{2}\pi ^{2}}{l^{2}}}{\frac {N}{\rho A}}\ }$

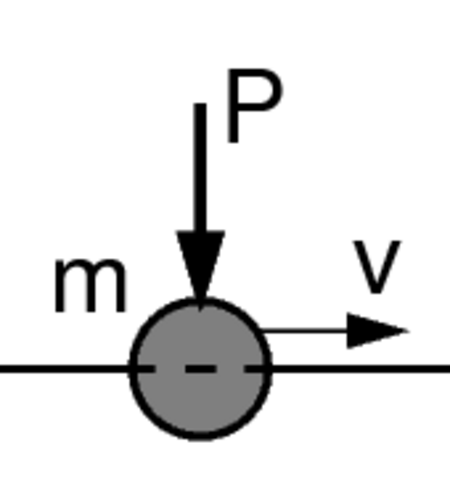
في حالة حمل متحرك ذو قوة قصور ذاتي يكون الحل التحليلي معروف، حيث يضاف حد لمعادلة الحركة لإضافة تأثير القصور الذاتي للحمل المتحرك، ويمكن نمذجته بكتلة مركزة m مصحوبة بقوة P تؤثر في نقطة كالتالي:

${\displaystyle -N{\frac {\partial ^{2}w(x,t)}{\partial x^{2}}}+\rho A{\frac {\partial ^{2}w(x,t)}{\partial t^{2}}}=\delta (x-vt)P-\delta (x-vt)m{\frac {{\mbox{d}}^{2}w(vt,t)}{{\mbox{d}}t^{2}}}\ }$

سرعة تقارب الحل عند استخدام عدد مختلف من حدود المتسلسلة.

بسبب صعوبة حساب الحد الأخير ففي العادة يتم إهماله من المهندسين، ويقتصر تأثير الحمل علي الترم الذي يهمل وجود كتلة للحمل. في بعض الحالات يتم وضع مذبذب في نقطة التلامس، هذا الحل مقبول فقط في حد السرعات القليلة للحمل. في حالة السرعات الكبيرة فإن كلا من مقدار وتذبذب الاهتزاز يتأثر بشكل كبير عند اهمال الكتلة.

المعادلات التفاضلية يمكن حلها برق شبه تحليلية فقط للمسائل البسيطة. حيث أن المتسلسلة المحددة للحل تصل لنهاية ثابتة بشكل جيد ووجد أن حساب 2-3 حدود يكفي في التطبيق. الحالات الأكثر تعقيدا يمكن حلها بطريقة العناصر المنتهية.

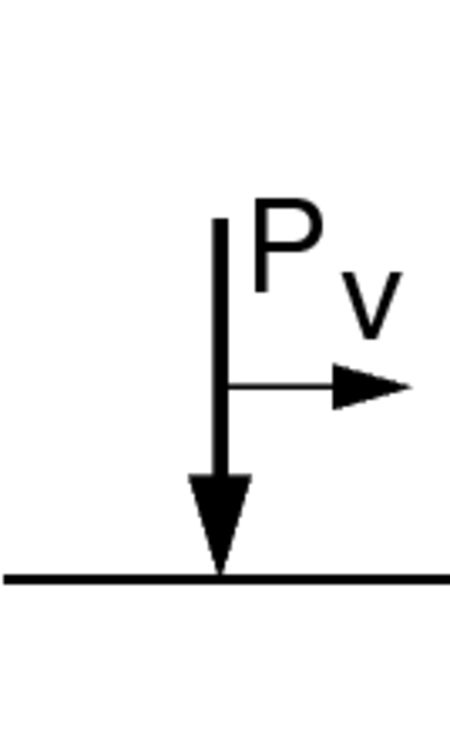
حمل بلا كتلة	حمل مصحوب بكتلة (قوة القصور الذاتي)
اهتزاز الوتر تحت تأثير حمل متحرك بلا كتلة (v=0.1c) حيث c هي سرعة الموجة. اهتزاز الوتر تحت تأثير حمل متحرك بلا كتلة (v=0.5c) حيث c هي سرعة الموجة.	اهتزاز الوتر تحت تأثير حمل متحرك مصحوب بكتلة (قوة القصور الذاتي) (v=0.1c) حيث c هي سرعة الموجة. اهتزاز الوتر تحت تأثير حمل متحرك مصحوب بكتلة (قوة القصور الذاتي) (v=0.5c) حيث c هي سرعة الموجة..

عدم التواصل في مسار الكتلة يبدو واضحا في حل معادلات كمرة توموشينكو. ويمكن تفسير الظاهرة بقوة جساءة القص.

الإهتزازات في كمرة توموشينكو: الخط الأحمر ـ محور الكمرة مع الزمن، الخط الأسود ـ مسار الكتلة (w₀- التشكل الاستاتيكي).

وتر بلا كتلة تحت تأثير حمل متحرك مصحوب بقوة قصور ذاتي

لنفرض وجود وتر بلا كتلة، والذي يعتبر حالة خاصة من مسألة الحمل المتحرك المصحوب بقوة قصور ذاتي. أول حل للمسألة قدم بواسطة Smith ^[7]، حيث قام بالتحليل متبعا خطوات حل Fryba.^[4] ، بفرض ρ=0 فإن معادلة الحركة تحت تأثير كتلة متحركة تكون

${\displaystyle -N{\frac {\partial ^{2}w(x,t)}{\partial x^{2}}}=\delta (x-vt)P-\delta (x-vt)\,m{\frac {{\mbox{d}}^{2}w(vt,t)}{{\mbox{d}}t^{2}}}\ }$

نقوم بإدخال حالات الحدود وهي ارتكاز بسيط لطرفي الوتر والحالة المبدأية بصفر حيث بدأ الوتر من السكون، لحل هذه المعادلة نستخدم خاصية الالتفاف، نفرض حركة للوتر غير معرفة بوحدة y ونفرض أيضا زمن غير معرف بوحدة τ:

وتر بلا كتلة و كتلة متحركه - مسار الكتلة.

${\displaystyle y(\tau )={\frac {w(vt,t)}{w_{st}}}\ ,\ \ \ \ \tau \ =\ {\frac {vt}{l}}\ }$

حيث w_st هو التشكل الاستاتيكي في منتصف الوتر، الحل يعطي بالمجموع:

${\displaystyle y(\tau )={\frac {4\,\alpha }{\alpha \,-\,1}}\,\tau \,(\tau -1)\,\sum _{k=1}^{\infty }\,\prod _{i=1}^{k}{\frac {(a+i-1)(b+i-1)}{c+i-1}}\;{\frac {\tau ^{k}}{k!}}\ }$

حيث α معامل ليس له وحده

${\displaystyle \alpha ={\frac {Nl}{2mv2}}\,>\,0\ \ \ \wedge \ \ \ \alpha \,\neq \,1\ }$

المعاملات a, b و c يمكن حسابهم من:

${\displaystyle a_{1,2}={\frac {3\,\pm \,{\sqrt {1+8\alpha }}}{2}}\ ,\ \ \ \ \ b_{1,2}={\frac {3\,\mp \,{\sqrt {1+8\alpha }}}{2}}\ ,\ \ \ \ \ c=2\ }$

وتر بلا كتلة و كتلة متحركه - مسار الكتلة, α=1.

في حالة α=1 فان المسألة لها حل تحليلي

${\displaystyle y(\tau )=\left[{\frac {4}{3}}\tau (1-\tau )-{\frac {4}{3}}\tau \left(1+2\tau \ln(1-\tau )+2\ln(1-\tau )\right)\right]\ }$

انظر ايضا

• حمل إنشائي.

• هندسة مدنية.
• إطار جاسئ.
• تكامل مباشر لكمرة.
• معامل تحميل.

مراجع

مصادر خاريجية

• Christopher F. Beards: Structural vibration: analysis and damping. E. Arnold, London 1996,
• Chang T. Sun, Yeh-Pei Lu: Vibration damping of structural elements. Prentice Hall, Englewood Cliffs 1995,
• Giancarlo Genta: Vibration of structures and machines: practical aspects. 3rd ed., Springer, New York 1999,
• Clarence W. De Silva: Vibration damping, control and design. CRC Press, Boca Raton, FL 2007,

موسوعات ذات صلة :

• موسوعة هندسة تطبيقية
• موسوعة عمارة
• موسوعة تقانة
• موسوعة تصميم