الرئيسيةعريقبحث

دالة تجزئة

☰ جدول المحتويات

تحدد دالة هاش الأسماء في صورة أرقام صحيحة من 0 إلى 15. لاحظ التصادم بين المفاتيح "جون سميث" و"ساندرا دي".

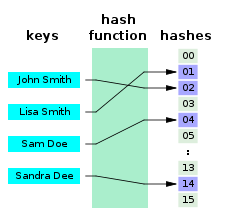
دالة تجزئة[1] أو دالة هاش (Hash function)‏ هي أي خوارزمية أو دالة رياضية تُحوِّل مجموعة كبيرة من البيانات إلى بيانات أصغر. وهي عادةً ما تكون عدد صحيح يعمل بمثابة مؤشر لمجموعة من البيانات. وتسمي القيم التي تسترجعها دالة هاش: قيم هاش أورموز هاش أو مجاميع هاش أو هاش. والفرق بين الهش والضغط أن الضغط يمكن فكه وإعادة البيانات إلى حجمها الأصلي لكن الهش لا يمكنه ذلك.فحين تهش البيانات لن يعود بالإمكان استرداد حجمها الأصلي.

تُستخدم دالات هاش غالباً لتطوير الجدول أو مهام البيانات مثل: العثور على العناصر الموجودة داخل قاعدة البيانات، والكشف عن صفوف مماثلة في ملف كبير، وإيجاد مساحات مماثلة في تسلسلات الدي إن إيه، وغيرها.

وقد تحدد دالة هاش مفتاح أو اثنين من مفاتيح قيمة هاش نفسها. وفي كثير من التطبيقات، يجب تقليل نسبة التصادم. وهذا يعني أنه يجب على دالة هاش رسم خريطة لمفاتيح قيم هاش بالتساوي قدر الإمكان. وقد تتطلب بعض التطبيقات خصائص أخرى. وعلى الرغم من أن الفكرة قد نشأت في الخمسينيات [2]، لا يزال موضوع تصميم دالات هاش قيد البحث.

ترتبط دالات هاش بتدقيق المجموع، وتدقيق الأرقام، والبصمات، والدالات العشوائية، ورموز تصحيح الخطأ، ودالة هاش الرمزية. وعلى الرغم من تداخل هذه المفاهيم إلى حدٍ ما، لكل مفهوم استخداماته واحتياجاته الخاصة. كما يتم تصميم كل واحدة منهم بشكل مختلف.

التطبيقات

جداول هاش

تُستخدم دالات هاش أساساً في جدول هاش لتحديد مكان تسجيل البيانات بسرعة (كتعريف في القاموس مثلاً) من خلال مفتاح البحث الخاص به (الكلمة المراد البحث عنها). ومن ثم تُستخدم دالة هاش لتحديد مفتاح البحث. ويُعطي المؤشر المكان الذي يجب تخزين البيانات فيه. وبالتالي، تُستخدم جداول هاش لتنفيذ مصفوفات ترابطية ومجموعات ديناميكية.

ويُمكن أن تحدد دالات هاش مفاتيح مختلفة لنفس المؤشر. ولذلك، يرتبط كل جزء من جدول هاش (بشكل مباشر أو غير مباشر) بمجموعة من التسجيلات بدلاً من تسجيل واحد. ولهذا السبب، يُسمى كل جزء من جدول هاش مجموعة، كما تُسمى قيم هاش أيضاً مؤشرات المجموعة.

وبالتالي، تُساعد دالة هاش فقط في تحديد موقع التسجيل—حيث تُحدد المكان الذي ينبغي بداية البحث منه. وبالتالي، ستُقلل دالة هاش من نطاق البحث إلى مدخل واحد فقط أو اثنين.

الخابية

تُستخدم دالة هاش أيضاً لبناء خابية لمجموعات البيانات الكبيرة المُخَزَّنَة في الوسائل البطيئة. وتُعتبر الخابية أبسط من جدول هاش. ذلك لأنه يُمكن حل أي اصطدام من خلال التخلص من العناصر المتصادمة الكبيرة.

فلاتر بلوم

دالات هاش هي عُنصر أساسي من عناصر فلتر بلوم. وهو بنية معقدة للبيانات تُوفر مكان لضم مجموعة من المفاتيح.

العثور على تسجيلات مكررة

يُمكن استخدام دالة هاش لإيجاد تسجيلات في ملف كبير من خلال رسم خريطة لكل تسجيل داخل الجدول Ti، ثم يجمع في كل مجموعة T قائمة من الأرقام لجميع التسجيلات ذات نفس القيمة هاش i. وعندما يكتمل الجدول، ستذهب أي تسجيلات مكررة إلى مجموعة واحدة. ومن ثم يُمكن إيجاد العناصر المكررة عن طريق مسح كل المجموعة Ti التي تحتوي على عضوين أو أكثر، وومقارنة هذه التسجيلات. ومن خلال جدول ذو حجم مُناسب، يُمكن أن تكون هذه الطريقة أسرع من أي طريقة أخرى (مثل فرز الملف ومقارنة جميع الأزواج المتتالية).

العثور على تسجيلات مشابهة

يُمكن استخدام دالات هاش أيضاً لتحديد تسجيلات الجدول ذو مفتاح مماثل لمفتاح معين، وليس متطابق معه، أو مجموعات من التسجيلات الموجودة في ملف كبير ذو مفاتيح مماثلة. ولهذا السبب، يحتاج المرء دالة هاش لتحديد المفاتيح المشابهة لقيم هاش التي تختلف بالقسمة m كحد أقصى، حيث تُشير m إلى عدد صحيح صغير (1 أو 2 مثلاً) في حالة إنشاء جدول T لجميع أرقام التسجيلات، وذلك باستخدام دالة هاش. ومن ثم ستنتقل التسجيلات المماثلة إلى نفس المجموعة، أو في مكان قريب منه. إذاً، لا يحتاج المرء سوى التحقق من التسجيلات الموجودة في كل مجموعة Ti في مقابل المجموعة T T+k، حيث تتراوح قيمة k بين -m وm.

وتشمل هذه الفئة ما يسمى بخوارزميات البصمة الصوتية التي تًستخدم لتحديد موقع المدخلات الصوتية المتشابهة في مجموعة كبيرة من الملفات الصوتية (كما في خدمة MusicBrainz لتحديد الأغاني). وبالتالي، يجب أن تكون دالة هاش حساسة قدر الإمكان لالتقاط البيانات أو نقل الأخطاء، بالإضافة إلى التغييرات "البسيطة" مثل التوقيت والحجم وضغط الملفات وغيرها.[3][3]

العثور على مجموعات فرعية مماثلة

يُمكن استخدام التقنيات نفسها لإيجاد مساحات متساوية أو متماثلة في مجموعة كبيرة من السلاسل مثل: مستودع الوثائق أو قاعدة البيانات الحيوية. وفي هذه الحالة، تنقسم سلاسل المدخلات إلى مجموعات أصغر كثيرة. ثم تُستخدم الدالة هاش للكشف عن القطع التي من المحتمل أن تكون متساوية على النحو الوارد أعلاه.

خوارزميات رابين وكارب هي خوارزمية للبحث المتسلسل تعمل في Big O notation. وهي تعتمد على استخدام الدالة هاش لمقارنة السلاسل.

هندسة هاش

يُستخدم هذا المبدأ على نطاق واسع في الرسوميات الحاسوبية والهندسة الرياضية الحاسوبية والعديد من التخصصات الأخرى، وذلك لحل العديد من مشكلات المسافات القريبة في السطح المنبسط أو ثلاثي الأبعاد مثل: العثور على أزواج قريبة في مجموعة من النقاط، أو صور مماثلة في قاعدة بيانات الصور وغيرها. وفي هذه التطبيقات، تُعتبر كل مجموعة من هذه المدخلات نوع من أنواع الفضاء المتري. ومن ثم يُمكن تفسير دالة هاش على أنها جزء من هذا الفضاء في شبكة من الخلايا. وغالباً ما يكون الجدول صف ذو مؤشرين أو أكثر (يُسمى ملف الشبكة، ومؤشر الشبكة، ومجموعة الشبكة، وغيرها من الأسماء المشابهة). ثم تعود دالة هاش في شكل مؤشر المجموعة. وتُعرف هذه الحالة الاستثنائية لدالة هاش باسم هندسة هاش أو أسلوب الشبكة. وتُستخدم هندسة هاش في مجال الاتصال عن بعد لتشفير وضغط الإشارات متعددة الأبعاد.

الخصائص

تُستخدم الدالات هاش لتلبية بعض الخصائص المذكورة أدناه. ملحوظة: تنطبق بعض الاحتياجات المختلفة على المفاهيم الأخرى ذات الصلة (دالات هاش الرمزية وغيرها).

التكلفة المنخفضة

يجب أن تكون تكاليف إنشاء دالة هاش منخفضة بما يكفي لإيجاد حل مفيد يعتمد على الدالة هاش مقارنةً بالأساليب البديلة. فعلى سبيل المثال، يمكن أن تُحدد خوارزميات البحث الثنائي موقع عنصر في جدول العناصر n من خلال log2 n. ولذلك، يُصبح حل جدول هاش أكثر كفاءةً من البحث الثنائي إلا إذا كانت تكاليف حوسبة الدالة هاش لمفتاح واحد أقل من تكاليف القيام بـlog2 n. ومع ذلك، لا يأخذ هذا المثال فرز مجموعة البيانات في الاعتبار. وتأخذ الخوارزميات السريعة جداً مثل التصنيف الدمجي وقتاً يصل إلى nlogn لفرز مجموعة من البيانات. ولذلك تقل كفاءة حلول البحث الثنائي مع زيادة وتيرة العناصر المضافة إلى مجموعة البيانات. ومن مميزات جداول هاش أنها لا تحتاج إلى فرز، مما يجعل تكلفة دالة هاش ثابتة بغض النظر عن معدل إضافة العناصر إلى مجموعة البيانات.

الحتمية

يجب أن تكون دالة هاش حتمية—أي يجب أن تُنتج لكل قيمة من المدخلات نفس قيمة هاش. فيجب أن تكون الدالة هاش بالمعنى الحسابي للمصطلح. ولا ينطبق هذا الشرط على دالات هاش التي تعتمد على المُتغيرات الخارجية مثل: مُولد العدد شبه العشوائي الذي يعتمد على الوقت من اليوم. كما أنه يستبعد الدالات التي تعتمد على عنوان الذاكرة المُستخدمة في حالة تغير هذا العنوان خلال العملية (كما قد يحدث في الأنظمة التي تستخدم وسائل معينة لجمع القمامة). على الرغم من أنه يمكن إعادة العملية من جديد في بعض الأحيان.

التماثل

يجب أن تُحدد الدالة هاش المدخلات المتوقعة بالتساوي قدر الإمكان خلال مجموعة الإنتاج. وهذا يعني أنه يجب إنتاج كل قيمة هاش بنفس الاحتمال. ويكمن السبب وراء ذلك في أن تكلفة الأساليب المُعتمدة على هذه الدالة ترتفع بشكل حاد مع زيادة عدد التصادمات (أزواج المدخلات التي يتم تحديدها في نفس القيمة). إذا كان هناك احتمال حدوث بعض قيم هاش بعينها، يجب على الجزء الأكبر من عمليات التطوير البحث في مجموعة أكبر من مدخلات الجدول المتصادمة.

ملحوظة: يتطلب هذا المعيار أن تكون القيمة موزعة بشكل متجانس، ولا يجب أن تكون عشوائية بأي شكل. وتُعتبر الدالة العشوائية مفيدة لدالة الهاش، ولكن لا يجب أن يكون العكس صحيحاً.

وغالباً ما تحتوى جداول هاش على مجموعة فرعية صغيرة فقط من المُدخلات الصحيحة. فعلى سبيل المثال، قد تحتوي قائمة أعضاء النادي على مئة اسم خارج مجموعة الأسماء الممكنة الكبيرة جداً. وفي هذه الحالة، يجب أن يحتفظ المعيار المماثل بجميع مجموعات المُدخلات الفرعية التي قد تكون موجودة في الجدول، وليس مجموعة المدخلات المُمْكِنة فقط.

إذا تم تطبيق الدالة هاش على المجموعة m في خانات الجدول n، يجب أن تقل احتمالية تلقي المجموعات لأكثر من m/n. وخاصةً إذا كانت قيمة m أقل من n. حيث يجب أن يحتوى عدد قليل من المجموعات على تسجيل أو اثنين. (لا يجب أن تحتوى المجموعة في "دالة هاش المثالية" على أكثر من تسجيل واحد؛ ولكن هناك عدد حتمي من التصادمات حتى لو كانت قيمة n أكبر بكثير من m.

عند اختبار دالة هاش، يُمكن تقييم تماثل توزيع قيم هاش باستخدام اختبار مربع كاي.[4]

متغيرات متعددة

وفي كثير من التطبيقات، قد تختلف قيم هاش عند كل تشغيل لأي برنامج، أو قد تتغير أثناء التشغيل نفسه (عندما يحتاج جدول هاش إلى التوسع). وفي هذه الحالة، يحتاج المرء إلى دالة هاش ذات عاملين متغيرين—بيانات الإدخال z والرقم n لقيم هاش المسموح بها.

ويظل الحل المشترك لحساب دالة هاش ثابتة ذات مجموعة كبيرة جداً من المتغيرات (من 0 إلى 2 32 -1 مثلاً) هو أن تُقسَّم النتيجة على n، ويُستخدم ما تبقى بعد عملية القسمة. وعند استخدام هذه الطريقة، يجب اختيار دالة هاش بحيث تكون النتيجة موزعة بالتساوي بين 0 وn-1 لأي n داخل التطبيق. واعتماداً على الدالة، قد تكون النتيجة المتبقية مماثلة في حالة قيمة معينة لـn، مثل الأعداد الفردية أو الأعداد الأولية.

تسوية البيانات

قد تحتوى بعض البيانات المُدخلة في بعض التطبيقات على مميزات لا ترتبط بأغراض المقارنة. فعلى سبيل المثال، من المهم تجاهل الفرق بين الحروف العلوية والسفلية عند البحث عن اسم شخص. وبالتالي، يجب استخدام دالة تتوافق مع معيار تكافؤ البيانات المُستخدم: يجب أن يؤدي أي اثنين من المُدخلات المتماثلة إلى نفس قيمة هاش. ويُمكن تحقيق ذلك عن طريق تسوية المُدخلات قبل تطبيق دالة هاش عليها من خلال كتابة كل الحروف بالشكل العلوي.

الاستمرارية

يجب أن تكون الدالة هاش المُستخدمة للبحث عن بيانات مماثلة دالة مستمرة بقدر الإمكان؛ يجب تحديد اثنين من المُدخلات التي تختلف قليلاً عند قيم هاش متساوية تقريباً.

ملحوظة: تُعتبر هذه الاستمرارية عادةً خطأ فادح في التحقق من المجموع، ودالات هاش الرمزية، وغيرها من المفاهيم. وتحتاج الدالة هاش الاستمرارية في بعض التطبيقات مثل جداول هاش التي تَستخدم البحث الخطي.

خوارزميات دالة هاش

يعتمد اختيار دالة هاش على طبيعة البيانات المدخلة بشكل كبير، وتوزيعها المحتمل في التطبيق.

دالة هاش البسيطة

إذا كانت البيانات التي سيُطبَّق عليها دالة هاش صغيرة بما يكفي، يُمكن استخدام البيانات نفسها باعتبارها قيمة هاش. وتبلغ تكلفة حوسبة دالة هاش "البسيطة" صفر (دالة متطابقة).

يعتمد مدى 'صغر' البيانات على مساحة الذاكرة المتوفر لجدول هاش. فقد يشمل جهاز كمبيوتر في عام 2008 مساحة متوفرة من الذاكرة بقيمة جيجا بايت، وهذا يعني أنه يمكنها استيعاب قيم هاش تصل إلى 30 بت. ومع ذلك، هناك العديد من التطبيقات التي يُمكن أن تعمل بأقل من ذلك. فعلى سبيل المثال، عند تحديد سلسلة أحرف بين الحالة العلوية والسفلية، يمكن استخدام الترميز الثنائي لكل حرف لفهرسة جدول يُوفِّر الشكل البديل لهذا الحرف ('A' لـ'a'، و'8' لـ'8'). وإذا تم تخزين كل حرف في 8 بت (كما هو الحال في آسكي)، يحتوى الجدول على 2 8 = 256 فقط من المُدخلات؛ أما في حالة حروف اليونيكود سيحتوى الجدول على 17 × 2 16 = 1114112 من المُدخلات.

ويمكن استخدام هذه التقنية نفسها لتحديد رموز البلاد التي تتكون من حرفين 'us' أو 'za' لأسماء البلاد (26 ² = 676 إدخال في الجدول). كما يمكن أن تظل قيم البيانات غير الصحيحة غير معروفة (مثل رمز البلد 'x x' أو الرمز البريدي 00000) في الجدول، أو يمكن تحديدها بقيمة أخرى مناسبة.

دالة هاش المثالية

دالة هاش مثالية للأربعة أسماء المُبَيَّنَة.

تُعتبر الدالة هاش المتباينة دالة مثالية. وهي التي تُوجه كل مُدخل صحيح إلى قيمة هاش مختلفة. ويمكن تحديد موقع الإدخال المطلوب مباشرةً في جدول هاش من خلال هذه الدالة دون اللجوء إلى أي بحث إضافي.

تُعد دالات هاش المثالية فعَّآلة فقط عندما تكون المُدخلات ثابتة ومعروفة سلفاً مثل: تحديد أسماء الشهور من خلال الأعداد الصحيحة من 0 إلى 11. ويُمكن تمثيل الدالة المثالية للمجموعة n في أقل من 3*n من خلال الدالة هاش المناسبة التي يمكن العثور عليها في الوقت الذي يتناسب مع n. كما يمكن تقييم تلك الدالة من خلال عدد ثابت من العمليات. وهناك مولدات تُنتج شفرة تنفيذية لتقييم دالة هاش المثالية لمجموعة معينة من المُدخلات.

الحد الأدنى من المثالية للدالة هاش

دالة هاش مثالية في حالتها الدنيا للأربعة أسماء المُبَيَّنَة.

تُعتبر الدالة هاش المثالية n في حالتها الدنيا إذا كانت مجموعتها تتألف من أعداد صحيحة متتالية n، عادةً من 0 إلى n-1. وتُنتج الدالة هاش أيضاً في هذه الحالة جدول هاش مُعقَّد دون وجود أي بنود فارغة، بالإضافة إلى توفير البحث من خلال خطوة واحدة. ويصعب العثور على دالات هاش المثالية في حالتها الدنيا بشكل كبير.

البيانت المُوزعة بالتساوي من خلال الدالة هاش

عندما تكون المدخلات مستقلة في شكل سلاسل ذات أطوال مختلفة (مثل أرقام الهواتف، ولوحات تسجيل المركبات، وأرقام الفواتير إلخ)، تحتاج الدالة هاش إلى تحديد نفس عدد مُدخلات القيم هاش. فعلى سبيل المثال، إذا كانت المُدخلات عبارة عن عدد صحيح z في المجموعة من 0 إلى N-1، يجب أن يكون الناتج عدداً صحيحاً h في المجموعة من 0 إلى n-1، حيث تكون قيمة N أكبر بكثير من n. وبالتالي، يمكن أن تكون الدالة هاش: h = z mod n (ما تبقى من z مقسوماً على n)، أو h = (z × n) ÷ N (خفض القيمة z بـ n/N لتصبح عدد صحيح)، أو غيرها من الصيغ الأخرى.

تطبيق الدالة هاش على البيانات من خلال توزيعات أخرى

لن تعمل هذه الصيغ البسيطة إذا لم تتساو مُدخلات القيم. فعلى سبيل المثال، يعيش معظم رواد أي مركز تجاري في نفس المنطقة الجغرافية، وبالتالي يتشابه أول 3 أو 4 أرقام لهواتفهم. وفي هذه الحالة، إذا كانت قيمة n تساوي 10000، ستَنتج تصادمات عديدة من صيغة القسمة: z × n ÷ N التي تعتمد بشكل كبير على الأرقام الرائدة. بينما يَنتج عن الصيغة المتبقية z mod n قيم هاش مُوزعة بشكل متساوي.

تطبيق الدالة هاش على البيانات متغيرة الطول

عندما تتكون قيم البيانات من سلاسل ذات أحرف طويلة (أو متغيرة الطول) مثل: أسماء الأشخاص، وعناوين الإنترنت، ورسائل البريد، يتم توزيعهم بشكل غير مُتساوي وتبعيات معقدة. فعلى سبيل المثال، يتميز النص في أي لغة طبيعية بتوزيع غير مُتساوي للحروف. وبالتالي، من المهم استخدام الدالة هاش التي تعتمد على كل حروف السلسلة عند التعامل مع هذه البيانات. كما يجب أن تعتمد على كل حرف بطريقة مختلفة.

وعادةً ما يُستخدم نظام ميركيل-دامجراد في دالات هاش الرمزية. وبصفة عامة، يتم تطبيق الدالة هاش على البيانات من خلال تقسيم المُدخلات إلى سلسلة من الوحدات الصغيرة (البت، والبايت، والكلمات إلخ)، ثم تجميع كل الوحدات b1، وb2...، وbm بالتتابع على النحو التالي:

S ← S0; // Initialize the state. for k in 1, 2, …, m do // Scan the input data units: S ← F(S, b[k]); // Combine data unit k into the state. return G(S, n) // Extract the hash value from the state.

كما يُستخدم هذا الأسلوب في كثير من النصوص الاختبارية وخوارزميات البصمات. ويُمكن أن يكون المتغير S عدد صحيح 32 أو 64 بت. وفي هذه الحالة، يمكن لـS0 أن تساوي 0، ويُمكن لـG:S,n أن تكون مجرد S mod n. ويعتمد أفضل اختيار لـF على طبيعة البيانات، وهي مسألة معقدة جداً. وإذا كانت وحدات b:k تتكون من بت واحد، يُمكن أن تُساوي F:S,b على سبيل المثال:

if highbit(S) = 0 then return 2 * S + b else return (2 * S + b) ^ P

> حيث يُشير highbit:S إلى أكثر بت مهم؛ بينما يدل المشغل '*' على عملية ضرب العدد الصحيح؛ وتشير '^' إلى عملية البت التي طُبِّقَت على الكلمات، وP هي كلمة مناسبة ثابتة.[5]

دالات هاش ذات أغراض خاصة

في كثير من الحالات، يُمكن تصميم دالة هاش لأغراض خاصة (خوارزمية الكشف عن مجريات الأمور). وذلك للحصول على عدد أقل من التصادمات. لنفترض أن مُدخلات البيانات عبارة عن أسماء ملفات مثل: FILE0000.CHK، وFILE0001.CHK، وFILE0002.CHK مع وجود أرقام متسلسلة. يجب استخدام دالة لاستخراج الجزء الرقمي k من اسم الملف، واسترجاع k mod n. وليس من الضروري أن يكون للدالة التي تم تطبيقها على نوع معين من البيانات نفس التأثير على توزيع البيانات بشكل مختلف.

وفي بعض التطبيقات مثل البحث الفرعي، يجب تصميم دالة هاش h لكل حرف فرعي k لسلsلة الأحرف n؛ حيث أن k هو عدد صحيح ثابت، وقيمة n أكبر بكثير من قيمة k. ويتطلب الحل المباشر تطبيق عدد من العمليات على k:n. ويكمن الحل في استخراج حرف فرعي s من t على حدة، وتصميم h:s. ومع ذلك، يمكن استخدام تقنية دالة هاش المتداولة لحوسبة جميع الدالات بجهد يتناسب مع k + n.

تطبيق هاش باستخدام الدالات الاختبارية

يمكن تكييف بعض الخوارزميات الاختبارية أو البصمات المعينة لتُستخدم كدلات هاش. وستُحدد بعض هذه الخوارزميات بيانات ذات سلسلة طويلة z وتوزيع نموذجي—سواء كان متساوي أم لا—من خلال سلسلة 32 بت أو 64 بت. ومن ثم يمكن استخراج قيمة هاش من 0 إلى 1-n.

ويمكن أن ينتج عن هذا الأسلوب توزيع موحد لقيم هاش ما دام حجم مجموعة هاش n صغير، مقارنةً بمجموعة الدالات الاختبارية. ومع ذلك، لا تنجح بعض المجاميع الاختبارية في اختبار الانهيار الأفالانشي في بعض التطبيقات. ويُوفر اختبار CRC32 الأكثر شعبيةً 16 بت فقط لاستخدامها في دالة هاش. بالإضافة إلى ذلك، تُؤثر كل بت من المُدخلات على بت واحد فقط من الـCRC32؛ لذا يجب الحرص على استخدام جميع الـ32 بت عند تصميم الدالة هاش.[6]

تطبيق هاش من خلال دالات هاش الرمزية

تتميز بعض دالات هاش الرمزية مثل SHA-1 بضمانات موحدة قوية أكثر من الدالات الاختبارية. وبالتالي، يمكنها أن توفر دالات هاش ذات أغراض عامة.

وفي التطبيقات العادية، يُعتبر هذا الأسلوب غير كافي لتعويض تكلفته المرتفعة.[7] ومع ذلك، يمكن أن تُوفر هذه الطريقة دالات هاش مُوزعة بشكل متجانس حتى في حالة اختيار المفاتيح من قبل عامل خبيث. وقد يُساعد هذا الأسلوب في حماية الخدمات ضد هجمات الحرمان من الخدمات.

أصل المصطلح

يأتي مصطلح "هاش (hash)" قياساً على معناه غير التقني: "الفرم والمزج". حيث تقوم دالات هاش "بتقسيم" مجموعة المُدخلات إلى مجموعات فرعية يتم "خلطها" في مجموعة الإنتاج لتحسين نظام التوزيع الرئيسي بشكل متساوي.

ذكر دونالد كانوث أن هانز بيتر لون من آي‌ بي‌ إم هو أول من استخدم هذا المصطلح. وذلك في مذكرة بتاريخ يناير عام 1953. كما استخدم روبرت موريس هذا المصطلح في ورقة بحث في مجلة رابطة مكائن الحوسبة، مما حوَّل المصطلح من لغة التكنولوجيا إلى اللغة الرسمية.[2]

قائمة دالات هاش

  • بيرنشتاين هاش [8]
  • دالة هاش فاولر-نول-فو (32 أو 64 أو أو 28 أو 256 أو 512 أو 1024 بت)
  • دالة هاش جنكينز (32 بت)
  • دالة هاش مورمور (32 أو 64 بت)
  • دالة هاش بيرسون (8 بت)
  • دالة هاش زوربيست

المراجع

  1. قاموس المعاني ترجمة كلمة Hash Function لدالة تجزئة تاريخ الولوج 18 أبريل 2013 نسخة محفوظة 17 يناير 2015 على موقع واي باك مشين.
  2. Knuth, Donald (1973). فن برمجة الحاسوب, volume 3, Sorting and Searching. صفحات 506–542.
  3. "Robust Audio Hashing for Content Identification by Jaap Haitsma, Ton Kalker and Job Oostveen" - تصفح: نسخة محفوظة 8 مايو 2020 على موقع واي باك مشين.
  4. بريت مولفي، دالات هاش 11 أبريل 2009 نسخة محفوظة 5 مايو 2020 على موقع واي باك مشين.
  5. إيه زيد برودور. بعض تطبيقات رابين لطريقة البصمات. في السلسلة الثانية: أساليب الاتصالات، والأمن، وعلوم الحاسب الآلي، صفحة 143--152. سبرينجر فيرلاج، 1993
  6. بريت مولفي، تقييم الـCRC32 لجداول هاش، في دالات هاش 10 أبريل 2009. نسخة محفوظة 5 مايو 2020 على موقع واي باك مشين.
  7. بريت مولفي، تقييم SHA-1 لجداول هاش، في دالات هاش. 10 أبريل 2009. نسخة محفوظة 5 مايو 2020 على موقع واي باك مشين.
  8. https://web.archive.org/web/20191227184627/http://www.cse.yorku.ca/~oz/hash.html. مؤرشف من الأصل في 27 ديسمبر 2019.

وصلات خارجية

موسوعات ذات صلة :