دالة

مخطط التابع ${\displaystyle {\begin{aligned}&\scriptstyle f\colon [-1,1.5]\to [-1,1.5]\\&\textstyle x\mapsto {\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}$

تمثيل بياني لدالة

رمز للدالة بشكل عام

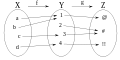
في الرياضيات، الدالة (الجمع: دَوَالّ) أو التابع أو الاقتران (Function)‏ هي كائن رياضي يمثل علاقة تربط كل عنصر من مجموعة تدعى المنطلق أو مجموعة الانطلاق أو المجال ${\displaystyle X\!}$ بعنصر واحد وواحد فقط على الأكثر من مجموعة تدعى المستقر أو المجال المقابل أو مجموعة الوصول ${\displaystyle Y\!}$.^[1][2][3] أو باستعمال الصياغة الرياضية الرسمية:${\displaystyle f\colon X\rightarrow Y,x\mapsto f(x)\!}$

ينتج عن هذا التعريف عدة أمور أساسية:

• لكل تابع مجموعة منطلق (أو نطاق) غالبا ما تدعى ${\displaystyle X\!}$.
• لكل تابع مجموعة مستقر (أو نطاق مرافق) غالبا ما تدعى ${\displaystyle Y\!}$.
• لا يمكن لعنصر من مجموعة المنطلق ${\displaystyle X\!}$ أن يرتبط إلا بعنصر وحيد من مجموعة المستقر ${\displaystyle Y\!}$.
• يمكن لعنصر من مجموعة المستقر ${\displaystyle Y\!}$ أن يرتبط بعنصر واحد أو أكثر من مجموعة المنطلق ${\displaystyle X\!}$.

فاذا كان المنطلق (النطاق) هو مجموعة القيم التي يمكن أن يأخذها متغير مستقل ${\displaystyle x}$، فإن المستقر أو (النطاق المرافق) هو مجموعة القيم الممكنة لقيم دالة ${\displaystyle f(x)\!}$.

غالبا ما نخصص لفظ دالة للتطبيقات التي يكون مستقرها ${\displaystyle \mathbb {R} }$ (الدوال العددية)، أو ${\displaystyle \mathbb {C} }$ (الدوال العقدية). في حين نسمي تطبيقا كل ما يحقق التعريف أعلاه.

الاقتران هو علاقة يرتبط بها كل عنصر من عناصر المجال بعنصر واحد فقط من عناصر المدى.

تعريف

بيان دالة حيث مجموعة الانطلاق X={1, 2, 3} ومجموعة الوصول Y={A, B, C, D}, which is defined by the set of ordered pairs {(1,D), (2,C), (3,C)}. The image/range is the set {C,D}.

---

---

---

هذا البيان ممثلا مجموعة الأزواج {(1,D), (2,B), (2,C)}، لا يعرف دالةdefine a function. One reason is that 2 is the first element in more than one ordered pair, (2, B) and (2, C), of this set. Two other reasons, also sufficient by themselves, is that neither 3 nor 4 are first elements (input) of any ordered pair therein.

أمثلة

التمثيل البياني لدالة هو منحنى بياني حيث صورة فاصلة كل نقطة منه تساوي ترتيبها فهذا التمثيل البياني للدالة ${\displaystyle f(x)=x^{2}-x-2\!}$

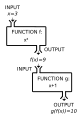
لتكن الدالة ${\displaystyle f\colon X\rightarrow Y,x\mapsto x^{2}\!}$

أي أن ${\displaystyle f(x)=x^{2}\!}$

بأخد ${\displaystyle x=2}$ نجد ${\displaystyle f(2)=4}$، هنا بالتعريف أعلاه اختُصرت الدالة التربيعية بالحرف ${\displaystyle f\!}$. عندئذ نجد أن العنصر${\displaystyle x=2}$ من المنطلق يرتبط بالعنصر ${\displaystyle y=4}$ من المستقر فقط. العنصر ${\displaystyle x=-2}$ من المنطلق (أو المجال)${\displaystyle X\!}$ يرتبط بالعنصر ${\displaystyle y=4}$ فقط من المستقر، فإذا من الممكن للعنصر ${\displaystyle y=4}$ من المستقر أن يرتبط بعنصرين ${\displaystyle x=2}$ و${\displaystyle x=-2}$ من المنطلق في حين أن أي عنصر من المنطلق يرتبط بعنصر واحد فقط من المستقر. هذا أمر جوهري في تحديد كون أي علاقة بين مجموعتين تشكل دالة رياضية.

بالمقابل ${\displaystyle \mathrm {Root} (x)=\pm {\sqrt {x}}}$ ليست دالة، لأنها تربط أي مدخل ${\displaystyle x}$ بمخرجين. مثل، الجذر التربيعي للعدد ${\displaystyle 9}$ قد يحتمل قيمتين هما ${\displaystyle 3}$ و${\displaystyle -3}$. لهذا، إذا أردنا أن نجعل الجذر التربيعي دالة فيجب أن نحدد أي جذر نختار، السالب أم الموجب. التعريف

${\displaystyle \mathrm {Posroot} (x)={\sqrt {x}},\quad \forall x\geq 0}$،

يعطي لأي مدخل غير سالب مخرجا واحدا فقط هو الجذر التربيعي الموجب.

${\displaystyle f(2)=2\cdot 2=4}$

مصطلحات

مجال الدالة

مجال دالة أو مجموعة تعريفها هو مجموعة جزئية من المنطلق حيث الدالةُ معرفةٌ. أي حيث الدالة تربط حتميا العنصر بمجموعة الانطلاق بعنصر من مجموعة الوصول. على سبيل المثال، دالة الجذر التربيعي لا تعرف إلا على الأعداد الموجبة. إذن مجموعة انطلاق هذه الدالة هي ℝ بينما مجالها فهو ℝ+.

مدى الدالة

مدى دالة هو مجموعة القيم الفعلية للدالة f. مدى الدالة هو مجموعة القيم المحتمل خروجها ناتجا للدالة بعد التعويض بالقيم الخاصة بمجال الدالة فمثلا f(x)=y=4x+1 فان هذه الدالة تتكون من مجال يمثل كل قيم x الممكنة اما مدى الدالة فهو يمثل كل قيم y المحتمل خروجها ناتجا للتعويض في هذه الدالة.

ويجب عدم الخلط بين المدى والمستقر حيث يمكن للدالة ألا تغطي جميع قيم المستقر فيكون المدى مجرد مجموعة جزئية من المستقر.

ما الدالة وما التطبيق ؟

عادة ما تسمى الدالة تطبيقا، ولكن هناك من الكتاب والعلماء من يضع فرقا بينهما. على سبيل المثال، فهناك من يعرف التطبيق دالةً إضافة إلى عدد من البُنى الخاصة.

انظر إلى نظام تحريكي وإلى تطبيق بوانكاري.

أنوع الدوال

هناك أنواع عديدة من الدوال.

الدوال الزوجية والدوال الفردية

إذا كانت دالة ما تعطي نفس النتيجة عندما تطبق على العدد وعلى مقابله، فإن هذه الدالة تسمى دالة زوجية. وإذا كانت تعطي قيمةً ما عندما تُطبق على عدد ما وتعطي مقابل هذه القيمة عندما تطبق على مقابل هذا العدد، فإن هذه الدالة تسمى دالة فردية.

الدوال الشمولية والدوال التباينية والدوال التقابلية

تكون دالة ما تقابلا، وقد يقال دالة تقابلية إذا كانت في آن واحد شمولية وتباينية. أما الدالة الشمولية فهي دالة تضمن وجود سابق لكل عنصر من عناصر مجموعة الوصول. وأما الدالة التباينية فهي كل دالة تضمن الاختلاف عند اختلاف المداخل.

إذا كانت الدالة f تقابلا، فإن لها دالة الدالة العكسية مجموعة انطلاقها هي مجموعة وصول الدالة f، ومجموعة وصولها هي مجموعة انطلاق f.

الدوال التزايدية والدوال التناقصية والدوال الرتيبة

الدوال التزايدية هن دوال تكبر قيمها عندما تكبر قيمة متغيرها والدوال التناقصية فهن دوال تنقص قيمها عندما تكبر قيمة متغيرها. وأما الدوال الرتيبة فهن الدوال اللائي يحافظن على ترتيب ما، أي أنهن إما تزايدية أو تناقصية وليس الصفتين معا.

الدوال الحقيقية والدوال المركبة

الدالة المركبة والدالة التحليلية

المتتاليات

إذا كانت مجموعة انطلاق دالة ما هو مجموعة الأعداد الصحيحة الطبيعية، فإن هذا الدالة تسمى متتالية.

الداول الذاتية الاستدعاء

هي دوال يُحتاج في تعريفها إلى استدعاء الدالة ذاتها، دالة العاملي مثالا.

أنواع أخرى

والدالة الثابتة والدالة المستمرة والدالة الضمنية والدالة الأسية والدالة الصريحة والدالة المتطابقة.

تاريخ

صاغ مصطلح «function» بالإنكليزية العالم غوتفريد لايبنتز في عام 1649 لوصف كميات تتعلق بالمنحنيات كالميل عند نقطة معينة من المنحني.

تم استخدام المصطلح بعدها من قبل عالم الرياضيات ليونهارد أويلر في منتصف القرن الثامن عشر لوصف التعابير والصيغ الرياضية التي تتضمن عدة وسائط رياضية.

معرض صور

مراجع

مقالات ذات صلة

• قائمة الدوال الرياضية
• تابع كوب-دوغلاس
• تابع الإنتاج
• دالة متعددة التعريف
• دالة متعددة القيم
• دالة تربيعية
• دالة تكعيبية
• دالة رباعية
• التكامل الوظيفي

موسوعات ذات صلة :

• موسوعة رياضيات
• موسوعة تحليل رياضي
• موسوعة جبر