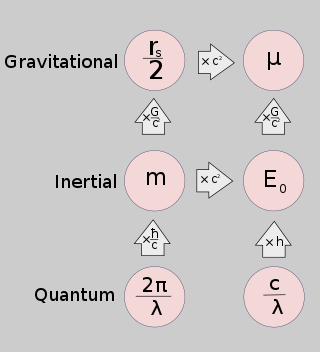
- نصف قطر شفارتزشيلد (rs) يمثل قدرة الكتلة على إحداث انحناء في الزمان والمكان.
- معامل الجاذبية القياسي (μ) يمثل قدرة الأجسام الضخمة لممارسة قوى الجاذبية النيوتونية على الأجسام الأخرى.
- الكتلة العطالية (m) تمثل الاستجابة النيوتونية للكتلة للقوى .
- الطاقة الساكنة (E0) تمثل قدرة تحول الكتلة إلى أشكال أخرى من الطاقة.
- طول موجة كومبتون (λ) يمثل الاستجابة الكمية للكتلة للهندسة المحلية (المكانية).
الكتلة الكوكبية هي مقدار كتلة كوكب أو جسم يشبه كوكب داخل النظام الشمسي. عادة ما تقاس الكواكب في نظام الوحدات الفلكي، حيث وحدة الكتلة هي الكتلة الشمسية (M☉) كتلة الشمس(M☉ = (1.98855±0.00025)×1030 كـغ[1][2]). وفي دراسة الكوكب خارج المجموعة الشمسية، وحدة القياس هي عادة كتلة كوكب المشتري (1.898×1027 كغم (MJ)[3]، للكواكب الغازية العملاقة وكتلة الأرض (M⊕) للكواكب الصخرية الصغيرة.كتلة الأرض = (5.9722±0.0006)×1024 كعم.[4][5]
القياس

الطريقة الفعالة التي يمكن من خلالها قياس كتلة كوكب هي من خلال جاذبيته. وكانت هذه هي الطريقة التي تم بها قياس كتلة الأرض[6]، ومع ذلك فإن قياس جاذبية الكواكب الأخرى، يعتمد على أساليب أخرى. وأكثر التقنيات استخدامًا هي مراقبة جسم يدور (قمر طبيعي) حول أو يمر بالقرب من كوكب ومراقبة تأثُّر مساره بجاذبية الكوكب.[6] ويمكن الاستدلال على كتلة الكوكب من تأثيره على مدارات الكواكب الأخرى. في 1931-1948 تطبيقات معيبة لهذا الأسلوب أدت إلى حسابات غير صحيحة لكتلة بلوتو. ويمكن استخدام البيانات التي تم جمعها لتأثر مدارات المسابر الفضائية. ومن الأمثلة مسباري فوياجر إلى الكواكب الخارجية والمركبة الفضائية ماسنجر إلى عطارد.
أيضًا، هناك العديد من الطرق الأخرى يمكن أن تعطي قيمة تقريبية معقولة للكتلة. على سبيل المثال، الكوكب القزم المحتمل، المعروف باسم فارونا، يدور بسرعة كبيرة على محوره، كما يفعل الكوكب القزم هوميا. فعلى سبيل المثال، يجب أن يكون هوميا كثيف جدًا حتى لا يتمزق بسبب دورانه السريع.[7]
اختيار الوحدات
اختيار الكتلة الشمسية، M☉، باعتبارها الوحدة الأساسية للكتلة الكوكبية يأتي مباشرة من الحسابات المستخدمة لتحديد الكتلة الكوكبية. وفي الحالة الأكثر دقة، حالة الأرض نفسها، تعرف الكتلة من حيث الكتلة الشمسية إلى اثني عشر رقم مهم تسهم في دقة القيمة: الكتلة نفسها، من حيث الكيلوغرامات أو الوحدات الأرضية الأخرى، معروفة فقط بخمسة أعداد معنوية، أقل من جزء من مليون على وجه التحديد.[5]
الفرق يأتي من الطريقة التي يتم حساب كتل الكواكب. فمن المستحيل أن "تزن" كوكب، والأصعب بكثير الشمس، عكس نوع معايير الكتلة التي تستخدم في المختبر. من ناحية أخرى، فإن مدارات الكواكب تعطي مجموعة كبيرة من البيانات الرصدية للمواقع النسبية لكل جسم، ويمكن مقارنة هذه المواقع مع كتلتها النسبية باستخدام قانون الجذب العام لنيوتن (مع تصحيحات صغيرة للنسبية العامة عند الضرورة). لتحويل هذه الكتلة النسبية إلى وحدات أرضية مثل الكيلوغرام، ومن الضروري معرفة قيمة ثابت الجاذبية، G. هذا الثابت عادة من الصعب قياسه بشكل ملحوظ وقيمته الدقيقة معروفة فقط لجزء واحد في عشرة آلاف.[8]
الكتلة الشمسية هي وحدة كبيرة جدًا على مقياس النظام الشمسي: 1.9884(2)×1030 كغم.[5] وأكبر كوكب، كوكب المشتري، كتلته 0.09٪ من كتلة الشمس، في حين أن كتلة الأرض حوالي ثلاثة ملايين جزء (0.0003٪) من كتلة الشمس.[5]
| الكوكب | عطارد | الزهرة | الأرض | المريخ | المشتري | زحل | أورانوس | نبتون |
|---|---|---|---|---|---|---|---|---|
| كتلة الأرض M⊕ | 0.06 | 0.82 | 1 | 0.11 | 317.8 | 95.2 | 14.6 | 17.2 |
| كتلة المشتري MJ | 0.000 17 | 0.002 56 | 0.003 15 | 0.000 34 | 1 | 0.299 | 0.046 | 0.054 |
قيم رزنامة مختبر الدفع النفاث
رزنامة مختبر الدفع النفاث [5][9] مستخدمة على نطاق واسع والتي يرجع تاريخها من عام 1998 وتغطي النظام الشمسي كله. وعلى هذا النحو، تشكل الكتل الكوكبية مجموعة متسقة ذاتيًا، وهذا ليس هو الحال دائمًا بالنسبة للبيانات الأكثر حداثة؛
| الكتلة الكوكبية × 10−6 (نسبة إلى الشمس) |
كتلة القمر (نسبة إلى الكوكب الأم) |
الكتلة المطلقة |
متوسط الكثافة | ||
|---|---|---|---|---|---|
| الكواكب والأقمار الطبيعية | |||||
| عطارد | 0.16601 | 3.301×1023 كغم | 5.43 جم/سم3 | ||
| الزهرة | 2.4478383 | 4.867×1024 كغم | 5.24 جم/سم3 | ||
| نظام الأرض / القمر | 3.04043263333 | 6.046×1024 كغم | 4.4309 | ||
| الأرض | 3.00348959632 | 5.972×1024 كغم | |||
| القمر | 1.23000383×10−2 | 7.346×1022 كغم | |||
| المريخ | 0.3227151 | 6.417×1023 كغم | 3.91 جم/سم3 | ||
| المشتري | 954.79194 | 1.899×1027 كغم | 1.24 جم/سم3 | ||
| آيو | 4.70×10−5 | 8.93×1022 كغم | |||
| أوروبا | 2.53×10−5 | 4.80×1022 كغم | |||
| غانيميد | 7.80×10−5 | 1.48×1023 كغم | |||
| كاليستو | 5.67×10−5 | 1.08×1023 كغم | |||
| زحل | 285.8860 | 5.685×1026 كغم | 0.62 جم/سم3 | ||
| تيتان | 2.37×10−4 | 1.35×1023 كغم | |||
| أورانوس | 43.66244 | 8.682×1025 كغم | 1.24 جم/سم3 | ||
| تيتانيا | 4.06×10−5 | 3.52×1021 كغم | |||
| أوبيرون | 3.47×10−5 | 3.01×1021 كغم | |||
| نبتون | 51.51389 | 1.024×1026 كغم | 1.61 جم/سم3 | ||
| ترايتون | 2.09×10−4 | 2.14×1022 كغم | |||
| الكواكب القزمة والكويكبات | |||||
| نظام بلوتو/شارون (قمر) | 0.007396 | 1.471×1022 كغم | 2.06 جم/سم3 | ||
| سيريس | 0.00047 | 9.3×1020 كغم | |||
| فيستا | 0.00013 | 2.6×1020 كغم | |||
| بالاس | 0.00010 | 2.0×1020 كغم | |||
القيم الأحدث
بناء رزنامة كاملة عالية الدقة للنظام الشمسي تعتبر مهمة شاقة.[10] ومن الممكن بناء رزنامة جزئية (أبسط) تتعلق فقط بالكواكب (أو الكواكب القزمة والأقمار والكويكبات) وتهتم "بتحديد" حركة الكواكب الأخرى في النموذج. والطريقتان ليستا متكافئتين تمامًا، لا سيما عندما يتعلق الأمر بتعيين مقدار النتائج المشكوك فيها: غير أن التقديرات "الأفضل" - بالنسبة لكتل الكواكب الصغيرة والكويكبات عادة ما تأتي من الرزنامة الجزئية.
ومع ذلك، لا يزال المفهوم الكامل لجداول وملفات بيانات المواقع المحسوبة للأجرام الفلكية قيد الإعداد. وأبرزها رزمانة الكواكب والقمر 2004 (EPM2004) من معهد علم الفلك التطبيقي التابع لأكادمية الروسية للعلوم.وتستند EPM2004 إلى أكثر من 317000 موقع مرصود بين عامي 1913 و2003 لأنواع مختلفة من الأجرام الفلكية، بما في ذلك القياسات الراديوية المترية للكواكب والمركبات الفضائية،[11] وهذه الجداول أكثر من سبعة أضعاف قدر جداول مختبر الدفع النفاث وتعطي كتلة أكثر دقة لسيريس وخمسة كويكبات أخرى.[10]
| EPM2004[10] | فيتاغليانو وستوس (2006)[12] |
براون وشالر (2007)[13] |
ثولن وآخرون. (2008)[14] |
بيتجيفا وستانديش (2009)[15] |
راجوزين وبراون (2009)[16] | |
|---|---|---|---|---|---|---|
| إريس | 84.0(1.0)×10−4 | |||||
| 134340 بلوتو | 73.224(15)×10−4 [note 1] | |||||
| 136108 هاوميا | 20.1(2)×10−4 | |||||
| 1 سيريس | 4.753(7)×10−4 | 4.72(3)×10−4 | ||||
| 4 فيستا | 1.344(1)×10−4 | 1.35(3)×10−4 | ||||
| 2 باللاس | 1.027(3)×10−4 | 1.03(3)×10−4 | ||||
| 15 إينوميا | 0.164(6)×10−4 | |||||
| 3 جونو | 0.151(3)×10−4 | |||||
| 7 ايريس | 0.063(1)×10−4 | |||||
| 324 بامبرغا | 0.055(1)×10−4 |
أفضل التقديرات الحالية للاتحاد الفلكي الدولي (2009)
تمت الموافقة على مجموعة جديدة من "أفضل التقديرات الحالية" لمختلف الثوابت الفلكية[17] في اجتماع الجمعية العامة السابعة والعشرين للاتحاد الفلكي الدولي في أغسطس 2009.[18] وتشمل كتل جميع الكواكب باستثناء نظام الأرض والقمر، وكذلك إيريس، بلوتو، سيريس، فيستا وبالاس: قيم كتل (ايريس، بلوتو، سيريس، فستا وبالاس) مبينة في الجدول أعلاه. باستثناء عطارد وأورانوس، تم تنقيح جميع كتل الكوكب منذ رزمانة جداول مختبر الدفع النفاث (DE405) لعام (1998).
| الكوكب | نسبة الكتلة الشمسية إلى كتلة الكوكب |
الكتلة الكوكبية × 10−6 (نسبة إلى الشمس) |
الكتلة (كغم) | مرجع |
|---|---|---|---|---|
| عطارد | 6023.6(3)×103 | 0.166014(8) | 3.3010(3)×1023 | [19] |
| الزهرة | 408.523719(8)×103 | 2.08106272(3) | 4.1380(4)×1024 | [20] |
| المريخ | 3098.70359(2)×103 | 0.3232371722(21) | 6.4273(6)×1023 | [21] |
| المشتري [note 2] | 1.0473486(17)×103 | 954.7919(15) | 1.89852(19)×1027 | [22] |
| زحل | 3.4979018(1)×103 | 285.885670(8) | 5.6846(6)×1026 | [23] |
| أورانوس | 22.90298(3)×103 | 43.66244(6) | 8.6819(9)×1025 | [24] |
| نبتون | 19.41226(3)×103 | 51.51384(8) | 1.02431(10)×1026 | [25] |
وتحدد نسبة كتلة القمر إلى كتلة الأرض على أنها: 1.23000371(4)×10−2,[15]، بينما يمكن حساب نسبة كتلة الشمس إلى كتلة الأرض كنسبة متعلّقة بمركز الشمس : 332.9460487(7)×103، مما يحدد كتلة الأرض عند: 3.003486962(6)×10−6 M☉ أو 5.9722(6)×1024 كلغم.[26]
ملاحظات
- لتسهيل المقارنة مع القيم الأخرى، فإن الكتلة الواردة في الجدول هي لنظام بلوتو بأكمله: وهذه هي أيضا القيمة التي تظهر في أفضل تقديرات الاتحاد الفلكي الدولي الحالية ،"كما تمنح تقديرات ثولن 'وغيره' كتل الأجسام الأربعة التي تشكل نظام بلوتو: بلوتو 6.558(28)×10−9 M☉, 1.304(5)×1022 kg; شارون 7.64(21)×10−10 M☉, 1.52(4)×1021 kg; نيكس 2.9×10−13 M☉, 5.8×1017 kg; هيدرا 1.6×10−13 M☉, 3.2×1017 kg.
- القيم المنشورة من فريق العمل التابع للاتحاد الفلكي الدولي والمعني بالمعايير العددية لدليل الفلك الأساسي (1.047348644×103) غير منسجمة مع قيمة الشك المعلنة (1.7×10−3): قيمة الكتل هنا تم تقريبها.
مصادر
- 2014 Astronomical Constants http://asa.usno.navy.mil/static/files/2014/Astronomical_Constants_2014.pdf
- NIST CODATA http://physics.nist.gov/cgi-bin/cuu/Value?bg
- Williams, Dr. David R. (2 November 2007). "Jupiter Fact Sheet". NASA. مؤرشف من الأصل في 20 يونيو 2019.
- "Solar System Exploration: Earth: Facts & Figures". NASA. 13 Dec 2012. مؤرشف من الأصل في 7 ديسمبر 201522 يناير 2012.
- "2016 Selected Astronomical Constants" in The Astronomical Almanac Online, United States Naval Observatory–United Kingdom Hydrographic Office . نسخة محفوظة 24 ديسمبر 2016 على موقع واي باك مشين.
- كيف تقيس كتلة الكوكب؟ - تصفح: نسخة محفوظة 05 يوليو 2017 على موقع واي باك مشين.
- "IAU names fifth dwarf planet Haumea". IAU Press Release. 2008-09-17. مؤرشف من الأصل في 25 أبريل 2014.
- Mohr, Peter J. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006" ( كتاب إلكتروني PDF ). Rev. Mod. Phys. 80: 633–730. doi:10.1103/RevModPhys.80.633. Direct link to value..
- Standish, E. M. (1998), JPL Planetary and Lunar Ephemerides, DE405/LE405 ( كتاب إلكتروني PDF ), JPL IOM 312.F-98-048 .
- Pitjeva, E. V. (2005), "High-Precision Ephemerides of Planets—EPM and Determination of Some Astronomical Constants" ( كتاب إلكتروني PDF ), Solar System Research, 39 (3): 176–86, Bibcode:2005SoSyR..39..176P, doi:10.1007/s11208-005-0033-2 .
- High-Precision Ephemerides of Planets—EPM and Determination of Some Astronomical Constants-May 2005, Volume 39, Issue 3, pp 176–186 - تصفح: نسخة محفوظة 09 يونيو 2018 على موقع واي باك مشين.
- Vitagliano, A.; Stoss, R. M. (2006), "New mass determination of (15) Eunomia based on a very close encounter with (50278) 2000CZ12", Astron. Astrophys., 455 (3): L29–31, Bibcode:2006A&A...455L..29V, doi:10.1051/0004-6361:20065760 .
- Brown, Michael E.; Schaller, Emily L. (15 June 2007). "The Mass of Dwarf Planet Eris". Science. 316 (5831): 1585. Bibcode:2007Sci...316.1585B. doi:10.1126/science.1139415. PMID 17569855.
- Tholen, David J.; Buie, Marc W.; Grundy, William M.; Elliott, Garrett T. (2008), "Masses of Nix and Hydra", Astron. J., 135 (3): 777–84, arXiv:, Bibcode:2008AJ....135..777T, doi:10.1088/0004-6256/135/3/777 .
- Pitjeva, E. V.; Standish, E. M. (2009), "Proposals for the masses of the three largest asteroids, the Moon-Earth mass ratio and the Astronomical Unit", Celest. Mech. Dyn. Astron., 103 (4): 365–72, Bibcode:2009CeMDA.103..365P, doi:10.1007/s10569-009-9203-8 .
- Ragozzine, Darin; Brown, Michael E. (2009), "Orbits and Masses of the Satellites of the Dwarf Planet Haumea = 2003 EL61", Astron. J., 137 (6): 4766–76, arXiv:, Bibcode:2009AJ....137.4766R, doi:10.1088/0004-6256/137/6/4766 .
- "The Final Session of the General Assembly" ( كتاب إلكتروني PDF ), Estrella d'Alva, صفحة 1, 2009-08-14 .
- Anderson, John D.; Colombo, Giuseppe; Esposito, Pasquale B.; Lau, Eunice L.; et al. (1987), "The Mass Gravity Field and Ephemeris of Mercury", Icarus, 71 (3): 337–49, Bibcode:1987Icar...71..337A, doi:10.1016/0019-1035(87)90033-9 .
- Konopliv, A. S.; Banerdt, W. B.; Sjogren, W. L. (1999), "Venus Gravity: 180th Degree and Order Model", Icarus, 139 (1): 3–18, Bibcode:1999Icar..139....3K, doi:10.1006/icar.1999.6086 .
- Konopliv, Alex S.; Yoder, Charles F.; Standish, E. Myles; Yuan, Dah-Ning; et al. (2006), "A global solution for the Mars static and seasonal gravity, Mars orientation, Phobos and Deimos masses, and Mars ephemeris", Icarus, 182 (1): 23–50, Bibcode:2006Icar..182...23K, doi:10.1016/j.icarus.2005.12.025 .
- Jacobson, R. A.; Haw, R. J.; McElrath, T. P.; Antreasian, P. G. (2000), "A Comprehensive Orbit Reconstruction for the Galileo Prime Mission in the J2000 System", J. Astronaut. Sci., 48 (4): 495–516 .
- Jacobson, R. A.; Antreasian, P. G.; Bordi, J. J.; Criddle, K. E.; et al. (2006), "The gravity field of the Saturnian system from satellite observations and spacecraft tracking data", Astron. J., 132 (6): 2520–26, Bibcode:2006AJ....132.2520J, doi:10.1086/508812 .
- Jacobson, R. A.; Campbell, J. K.; Taylor, A. H.; Synott, S. P. (1992), "The Masses of Uranus and its Major Satellites from Voyager Tracking Data and Earth-based Uranian Satellite Data", Astron. J., 103 (6): 2068–78, Bibcode:1992AJ....103.2068J, doi:10.1086/116211 .
- Jacobson, R. A. (3 April 2009). "The Orbits of the Neptunian Satellites and the Orientation of the Pole of Neptune". المجلة الفلكية. 137 (5): 4322–4329. Bibcode:2009AJ....137.4322J. doi:10.1088/0004-6256/137/5/4322.
- Ries, J. C.; Eanes, R. J.; Shum, C. K.; Watkins, M. M. (1992), "Progress in the Determination of the Gravitational Coefficient of the Earth", Geophys. Res. Lett., 19 (6): 529–31, Bibcode:1992GeoRL..19..529R, doi:10.1029/92GL00259 .