في التفاضل والتكامل، تنص مبرهنة رول على أن كل دالة قيمها عبارة عن أعداد حقيقية وقابلة للاشتقاق، والتي تتساوى قيمتها عند نقطتين اثنتين مختلفتين، فإن لهذه الدالة نقطة ما بينهما، حيث تكون قيمة اشتقاق الدالة مساوية للصفر.[1][2][3]
إذا كانت دالة تحقق الشروط الآتية لعددين حقيقيين a وb بحيث
- الدالة متصلة في المجال المغلق
- الدالة قابلة للاشتقاق في المجال المفتوح
فإنه يوجد عنصر c حقيقي ضمن بحيث .
الصيغة الرسمية للمبرهنة
تكتب مبرهنة رول على الشكل التالي:
مبرهنة — لتكن a و b عددين حقيقين حيث a < b و f دالة للقيم الحقيقية متصلة على [a, b] و قابلة للإشتقاق على ]a, b[ حيث يوجد (على الأقل) عدد حقيقي c ينتمي إلى ]a, b[ حيث
التاريخ
أول برهان رسمي معروف لهذه المبرهنة يعود إلى ميشيل رول. كان ذلك في عام 1691
أمثلة
المثال الأول
ليكن r عددا موجبا ولتكن الدالة التالية:
المثال الثاني
تعميمات
برهان الصيغة المعممة
تعميم لدرجات اشتقاق أعلى
برهان
وجود القيمة r يعني أن هناك قيمة قصوى أو دنيا. نفترض f موجبة في (أ، ب).
في هذه الحالة يكون للدالة f على الأقل قيمة قصوية.
إذا افترضنا أنه لا توجد القيمة r، وf(a) = 0 وf موجبة. فهذا يعني أن الدالة f متزايدة أي أن f(b)#0 وهذا يتناقض مع f(b)=0.
تعميمات لحقول أخرى
انظر أيضاً
مراجع
- "معلومات عن مبرهنة رول على موقع brilliant.org". brilliant.org. مؤرشف من الأصل في 11 فبراير 2018.
- "معلومات عن مبرهنة رول على موقع britannica.com". britannica.com. مؤرشف من الأصل في 1 أغسطس 2017.
- "معلومات عن مبرهنة رول على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 13 نوفمبر 2018.
- نظرية رول [1]








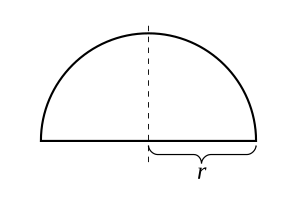
![{\displaystyle f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7ef1f348169f09e9db96b68d4b2e73d5f43c156)

![{\displaystyle f(x)=|x|,\qquad x\in [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/106570318bb857ac95a60c075c30a0f40dde84fe)