دالة أسية

الدالة الأسية (Exponential function)‏ هي كل دالة تُكتب على الشكل ${\displaystyle f(x)=a^{x}}$ حيث ${\displaystyle x\in \mathbb {R} }$ و ${\displaystyle a}$ عدد حقيقي موجب لا يساوي 1، إذا كان ${\displaystyle 0<a<1}$ فإن الدالة ${\displaystyle a^{x}}$ تكون تناقصية وتسمى دالة تضاؤل أسي، أما إذا كان ${\displaystyle a>1}$ فإن الدالة تكون تزايدية وتسمى دالة نمو أسي.^[1][2][3]

دالة أسية
تمثيل الدوال الأسية في جملة الإحداثيات الديكارتيّة، فاللون الأسود ذو الأساس (e)، واللون الأحمر ذو الأساس 10، واللون الأزرق ذو الأساس 1/2، نلاحظ أن جميع المنحنيات قطعت النقطة (0، 1).
ترميز	${\displaystyle a^{x}}$ أو ${\displaystyle \exp _{a}(x)}$
دالة عكسية	${\displaystyle \log _{a}(x)}$
مشتق الدالة	${\displaystyle \ln(a)a^{x}}$
مشتق عكسي (تكامل)	${\displaystyle {\frac {a^{x}}{\ln(a)}}+C}$
الميزات الأساسية
مجال الدالة	${\displaystyle \mathbb {R} }$
المجال المقابل	${\displaystyle \mathbb {R} _{+}^{*}}$
قيم محددة
القيمة/النهاية عند الصفر	1
نهاية الدالة عند +∞	${\displaystyle +\infty }$ إذا كان ${\displaystyle a>1}$ ${\displaystyle 0}$ إذا كان ${\displaystyle a<1}$
نهاية الدالة عند -∞	${\displaystyle 0}$ إذا كان ${\displaystyle a>1}$ ${\displaystyle +\infty }$ إذا كان ${\displaystyle a<1}$
القيمة/النهاية عند 1	${\displaystyle a}$
خطوط مقاربة	${\displaystyle y=0}$

الدالة الأسية تكاد تكون أفقية عند القيم السلبية للأس عندما يكون الأساس أكبر قطعا من الواحد، ثم تتزايد بسرعة في القيم الإيجابية، وتساوي 1 عندما تساوي قيمة x الصفر.

دوال أسية أخرى

${\displaystyle f(x)=a^{x}+b^{2}x}$ أو

${\displaystyle f(x)=a^{x}+5.M^{x}-3}$ أو

${\displaystyle f(x)=a^{x}+e^{x}}$

مثال آخر للدالة الأسية :

y = ل مرفوعة للقوة x ، وتكتب رياضيا كالآتي:

y=ل^x

حيث ل> صفر.

أي أن الدالة الأسية بصفة عامة :

X=yⁿ

تستخدم في الحاسوب معادلة أسية خاصة اسمها (exp(n. وهي تعادل حالة خاصة للمعادلة الأسية التي هي أصلا ${\displaystyle e^{n}}$ حيث e هو الثابت الطبيعي المسمى عدد أويلر. ذلك لأن الحالة الخاصة ${\displaystyle e^{n}}$ لها استخدامات واسعة في الفيزياء والكيمياء والهندسة الكهربائية والهندسة الميكانيكية والإحصاء وغيرها من العلوم. بعض الدول العربية تستخدم "هـ" بدلا عن e.

خواص الأسس

مشتق الدالة الأسية ${\displaystyle e^{n}}$ مساو لقيمة الدالة. لكل نقطة من المنحنى (الأزرق)، إذا رسم الخط المماس (الأحمر) والخط العمودي (الأخضر) كما هو مبين، فستكون للمثلث الذي يحددانه مع المحور الأفقي قاعدة طولها 1 (الأخضر). فيكون انحدار الخط المماس (المشتق) في النقطة مساويا لارتفاع المثلث (قيمة الدالة).

التعريف الجبري للدالة الأسية هو أنها تحول المجموع إلى جداء.

من خواص الدالة الأسية :

a⁰=1

a¹=a

الدالة العكسية للدالة الأسية هي اللوغاريتم (log) ذو الأساس a حيث تحول ${\displaystyle a^{x}}$ إلى x وهي تحول الجداء إلى مجموع :

${\displaystyle \log(a^{x})=x\log(a)}$

حيث x عدد حقيقي. الرمز log في هذه المقالة ينطبق على اللوغاريتم للأساس 10.

يمكن تحويل الدالة الأسية ${\displaystyle a^{x}}$ إلى أي أساس آخر ${\displaystyle b}$ :

${\displaystyle a^{x}=b^{x\cdot \log _{b}(a)}}$

وتنطبق القوانين التالية عليها :

${\displaystyle a^{0}=1\,}$...و... ${\displaystyle a^{1}=a\,}$

${\displaystyle a^{x+y}=a^{x}\cdot a^{y}}$

${\displaystyle a^{x\cdot y}=(a^{x})^{y}}$

${\displaystyle a^{-x}={\frac {1}{a^{x}}}=\left({\frac {1}{a}}\right)^{x}}$

${\displaystyle a^{x}\cdot \ b^{x}=(a\cdot \ b)^{x}}$

وتنطبق تلك القوانين على كل الأساسيات الحقيقية الموجبة ${\displaystyle a\,}$ و${\displaystyle b\,}$ وعلى جميع الأساسيات الحقيقية والمركبة ${\displaystyle x}$.

من أهم الدوال الأسية المستعملة في العلوم مثل كالفيزياء النووية والفيزياء الذرية والكهرباء والهندسة الكهربائية هي الدالة ذات الأساس e أي ${\displaystyle e^{x}}$ واللوغاريتم المنتسب إليها يرمز له بالرمز ln ، ويسمى "اللوغاريتم الطبيعي".

الدالة الأسية للأساس e هي الدالة الوحيدة التي تحقق الشرطين :

${\displaystyle f'=f}$

${\displaystyle f(0)=1}$

أي أنها حل للمعادلة التفاضلية من الدرجة الأولى.

الدالة الأسية للثابت الطبيعي e

دالة الأس الطبيعي
تمثيل دالة الأس الطبيعي
ترميز	${\displaystyle e^{x}}$ أو ${\displaystyle \exp(x)}$
دالة عكسية	${\displaystyle \ln(x)}$
مشتق الدالة	${\displaystyle e^{x}}$
مشتق عكسي (تكامل)	${\displaystyle e^{x}+C}$
الميزات الأساسية
مجال الدالة	${\displaystyle \mathbb {R} }$
المجال المقابل	${\displaystyle \mathbb {R} _{+}^{*}}$
قيم محددة
القيمة/النهاية عند الصفر	1
نهاية الدالة عند +∞	${\displaystyle +\infty }$
نهاية الدالة عند -∞	${\displaystyle 0}$
القيمة/النهاية عند 1	e
خطوط مقاربة	${\displaystyle y=0}$

هناك الحالة الخاصة عندما يكون الأساس هو الثابت الطبيعي e (تستخدم بعض البلاد العربية الثابت الطبيعي "هـ" بدلا عن المعترف به عالميا e).

وتكتب باللغة الإنجليزية:

(x=exp(n

حيث n هو الأُس للأساس الثابت الطبيعي الثابت «ه» والذي يساوي 2.718281828

وتوجد في الآلات الحاسبة لكثرة استعمالها.

أو بالتفصيل :

x=eⁿ

من خصائص الدالة الأسية للأساس الطبيعي e الخصائص التالية:

${\displaystyle \exp(x+y)=\exp(x)\cdot \exp(y)}$

${\displaystyle a^{x}:=\exp(x\cdot \ln a)}$

${\displaystyle a^{x}:=e^{x\cdot \ln a}}$

وذلك لجميع ${\displaystyle a>0}$ وجميع ${\displaystyle x}$ الحقيقية والمركبة.(ln a هو اللوغاريتم الطبيعي للأساس الطبيعي e وليس اللوغاريتم للأساس 10)

تزايد جهد المكثف مع الزمن يتبع دالة أسية للأساس e.

للدالة الأسية للأساس الطبيعي e أهمية كبرى في الفيزياء (مثل :تناقص الضغط الجوي بالارتفاع عن سطح الأرض [أنظر أسفله]) ، وفي الكيمياء (مثل : اعتماد سرعة التفاعل على درجة الحرارة)

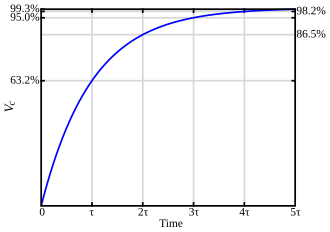
وفي الفيزياء بالنسبة إلى الدارة الإلكترونية حيث تتزايد مثلا شحنة مكثف طبقا للدالة الأسية مع الزمن x=eⁿ حيث n=t.c حتى تكتمل سعة المكثف. وإذا عملنا على تفريغ المكثف من شحنته يتبع معدل تفريغ الشحنة مع الزمن نفس الدالة الأسية الطبيعية مع جعل الأس بالسالب، أي x=e^-t.c.

• ويكون الأس n دائما عددا لا بعديا ، لكنه يتكون عادة من جزئين، ففي حالة المكثف الكهربائي على سبيل المثال يكون n=t.c حيث t الزمن ثانية و c خاصية للمكثف وحدتها [1/ثانية] ، وينتج عن حاصل ضربهما عددا لا بعديا.
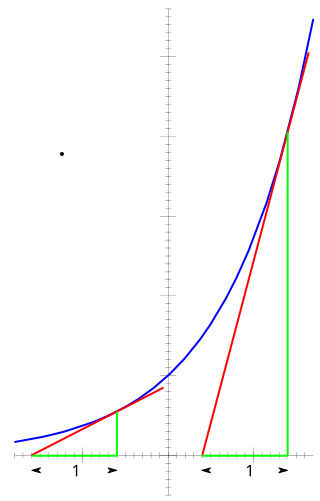
• يعطينا الشكل المجاور الشكل المميز للدالة الأسية للأساس e. وطبقا لها تتغير الشحنة الكهربائية الواردة على المكثف مع الزمن حتى يمتلئ تماما.

تعريفات أساسية للدالة الأسية للأساس e

يمكن تعريف الدالة الأسية للأساس e بعدة طرق متكافئة، على وجه التخصيص يمكن تعريفها بإستعمال متسلسلة قوى:

${\displaystyle \displaystyle e^{x}=\sum _{n=0}^{\infty }{\dfrac {x^{n}}{n!}}=1+x+{\dfrac {x^{2}}{2!}}+{\dfrac {x^{3}}{3!}}+{\dfrac {x^{4}}{4!}}+\cdots }$

أقل شيوعا يمكن تعريف e^x كحل للمعادلة التالية:

${\displaystyle \displaystyle x=\int _{1}^{y}{\dfrac {\mathrm {d} t}{t}}.}$

هي أيضا تساوي النهاية التالية:

${\displaystyle \displaystyle e^{x}=\lim \limits _{n\to \infty }\left(1+{\dfrac {x}{n}}\right)^{n}.}$

مشتقة الدالة الأسية للأساس e

تتميز الدالة الأسية للأساس e بكونها مساوية لمشتقتها التفاضلية :

${\displaystyle {\frac {\mbox{d}}{{\mbox{d}}x}}\exp(x)=\exp(x)}$

وعندما نختار لها الشرط :

${\displaystyle \exp(0)=1\;}$

تصبح الدالة الأسية للثابت الطبيعي e هي الوحيدة التي تفي بذلك الشرطين. بذلك يمكن تعريف الدالة الأسية الطبيعية بأنها حل تلك المعادلة التفاضلية. عندما تكون ${\displaystyle a>0}$ ينتج :

${\displaystyle a^{x}=\exp(x\cdot \ln a)}$

حيث ln a هو اللوغاريتم للأساس الطبيعي e وتنطبق المعادلة :

${\displaystyle {\frac {\mbox{d}}{{\mbox{d}}x}}a^{b\cdot x}=b\ln a\cdot a^{b\cdot x}}$

وفي هذه المعادلة لا يلزم استبدال اللوغاريتم الطبيعي بأي لوغاريتم لأساس آخر، حيث يأتي العدد e في حساب التفاضل بطريقة "طبيعية" من نفسه.

المعادلة التفاضلية من النوع ${\displaystyle {\frac {dy}{dx}}=ay+b}$ حيث a و b عددان حقيقيان

دالة أسية للأساس e: ثلاثة منحنيات للتحلل الإشعاعي لثلاثة مواد لها عمر النصف مختلف.

إن حل هذه المعادلة التفاضلية عبارة عن دالة أسية بحيث ${\displaystyle y(x)=\lambda e^{ax}-{\frac {b}{a}}}$ حيث ${\displaystyle \lambda }$ ثابتة حقيقية تحدد بالاعتماد على الشروط البدئية

مثال:

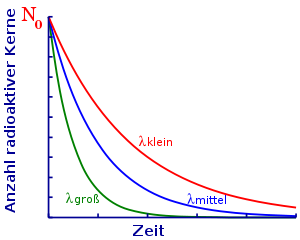
قانون التحلل الإشعاعي لنواة الذرة:

${\displaystyle N(t)=N_{0}\,e^{-{\lambda }t}\,\!}$

وتعطينا تلك المعادلة الأسية عدد الأنوية (N(t التي لم تتحلل بعد مرور الزمن t من مجموع أنوية الذرات N_0 الكلي عند البداية (عند t=0).

وتعتمد :${\displaystyle {\lambda }\!}$ على نوع الذرات الموجودة في العينة، وهي خاصية من خصائص العنصر المشع، وتختلف لليورانيوم عن البلوتونيوم وعن البوتاسيوم-40 مثلا. ووحدتها 1/ثانية.

المجاميع أسية

ليكن ${\displaystyle a}$ عنصرا من مجموعة الأعداد الحقيقية حيث ${\displaystyle a>1}$

المجموع الأول

${\displaystyle \sum _{i=0}^{n-1}{a^{i}}=a^{0}+a^{1}+a^{2}+\dots +a^{n-1}={\frac {a^{n}-1}{a-1}}}$

نهاية هذا المجموع

${\displaystyle \lim _{n\rightarrow \infty }{\sum _{i=1}^{n}}{a^{i}}=+\infty }$

المجموع الثاني

${\displaystyle \sum _{i=0}^{n}{\frac {1}{a^{i}}}={\frac {1-a^{n+1}}{a^{n}-a^{n+1}}}={\frac {a^{-n}-a}{1-a}}}$

نهاية هذا المجموع

${\displaystyle \lim _{n\rightarrow \infty }{\sum _{i=0}^{n}}{\frac {1}{a^{i}}}=\sum _{i=0}^{\infty }{a^{-i}}={\frac {a}{a-1}}}$

أمثلة

مثال للدالة الأسية بصفة عامة

تزايد الميكروبات : ينقسم الميكروب إلى نصفين مكونا ميكروبين، وينقسم كل منهما إلى نصفين فيصبحوا أربعة ميكروبات. ثم تنقسم الأربعة ميكروبات وتصبح ثمانية ميكروبات.

أي يبلغ عدد الميكروبات بعد 3 انقسامات :

N=2³

N=8

فإذا أردنا معرفة عدد الميكروبات بعد 6 انقسامات، صغنا المعادلة كالآتي:

N=2⁶

N=64

أي أن عدد الميكروبات الناتجة عن ميكروب واحد بعد ستة انقسامات يبلغ 64 ميكروبا.

امثلة للدالة الأسية للأساس الطبيعي e

التزايد السكاني :

يبلغ عدد سكان إحدى المدن 4 ملايين نسمة، فما عدد سكان المدينة بعد ستة سنوات إذا كان معدل تزايد السكان السنوي 2,5 %؟

نكتب المعادلة الآتي:

N=4. e^0,025.6

أو :

(N=4. Exp(0,025.6

والنتيجة :

مليون نسمة N=4,647 بعد 6 سنوات.

مثال 3 :

تكوّن النجوم : تتزايد كتلة أحد النجوم عن طريق اجتذابه للمادة حوله بمعدل 2 و0 % سنويا، فما تكون كتلته بعد 170 سنة ؟.

N=1. e^0,002.170

N=1. e^0,34

باستخدام الحاسوب نحصل على زيادة كتلته بنسبة 4 و1 خلال 170 سنة.

مثال 4:

تغير كثافة الهواء بالارتفاع عن سطح الأرض. المعادلة هي :

${\displaystyle {\rho }=\rho _{b}\cdot \exp \left[{\frac {-g_{0}\cdot M\cdot (h-h_{b})}{R^{*}\cdot T_{b}}}\right]}$

حيث الارتفاع h والارتفاع عند سطح الأرض ${\displaystyle \ (h_{b})}$.

(أنظر تغير الضغط بالارتفاع)

اقرأ أيضاً

• الدوال الإبتدائية
• تغير الضغط بالارتفاع
• توزيع بولتزمان
• احصاء ماكسويل-بولتزمان
• تجانس
• اختبار الوحدات

مراجع

موسوعات ذات صلة :

• موسوعة رياضيات
• موسوعة تحليل رياضي