العناصر المدارية هي المعلمات المطلوبة لتحديد مدار محدد على نحو فريد. في الميكانيكا السماوية هذه المعلمات تأخذ بعين الاعتبار بشكل عام في النظم الكلاسيكية ذات الجسمين، حيثما يتم استخدام مدار كبلر. هناك العديد من الطرق المختلفة لوصف نفس المدار رياضيا، ولكن هناك أنظمة معينة والتي يتألف كل منها من مجموعة ستة معلمات تكون كافية للوصف المدار وحركة الجرم الفلكي وتستخدم عادة في علم الفلك والميكانيكا المدارية.
يتغير المدار الحقيقي (وعناصره) بمرور الوقت بسبب الاضطرابات الجاذبية بواسطة الأجسام الأخرى وتأثيرات النسبية. المدار الكبلري هو مجرد مدار مثالي، وتقدير رياضي في وقت معين.
العناصر المدارية الكلاسيكية
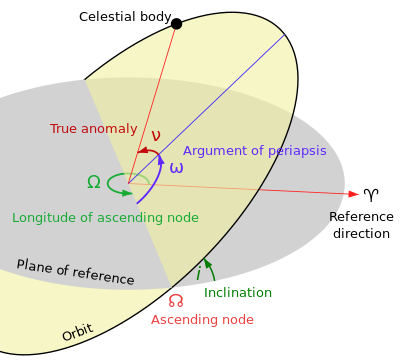
العناصر المدارية الكلاسيكية هي العناصر الكبلرية الستة، نسبة ليوهانس كيبلر وقوانينه فيما يتعلق بحركة الكواكب، هي المعلمات التي يمكن تحديدها لكل مرحلة من مراحل المدار، وعادة ما يشار إليها في وقت معين، أو حقبة معينة، وإطار مرجعي.[1] وفيما يلي تعاريف القيم التي تشكل العناصر المدارية الكلاسيكية: العناصر الرئيسية التي تحدد شكل وحجم القطع الناقص (إهليلجى):
- متوسط المسافة (a) - نصف-المحور الرئيسي للمدار المقاس بالوحدات الفلكية (1 = 149,59787 مليون كم)؛
- الانحراف (ه) - الانحراف المخروطي أو شكل المخروط، واصفا كم هو ممدود بالمقارنة مع دائرة (0 = دائرة، <1 = القطع الناقص، 1 = القطع المكافئ،> 1 = القطع الزائد) الذي يصف المدار.
وهناك عنصران يحددان اتجاه المستوي المداري :
- الميل (i) - الزاوية بين المستوي الإهليلجي ومستوى المدار.
- خط طول العقدة الصاعدة (Omega) - موقع في المدار حيث يمر المسار من خلال المستوى الكسوفي، من أسفل المستوى إلى فوق المستوى، ويقاس من الاعتدال الربيعي (النقطة الأولى من الحمل).
وأخيرا:
- حجة القبوة الحضيضية (w) - زاوية مستوي المدار من العقدة الصاعدة إلى النقطة التي يكون فيها الجرم أقرب إلى الشمس.
- الشذوذ الحقيقي (TA) - الزاوية الفعلية بين موقع الجرم ونقطة الحضيض . كما ترى من الشمس. هذه الزاوية تزداد بشكل غير موحد مع الوقت، وتغيير بسرعة أكبر في الحضيض.
- متوسط الشذوذ (M) -هي زيادة زاوية بشكل موحد مع مرور الوقت من خلال 360 درجة في الفترة المدارية من 0 عند الحضيض.
ويمكن أيضا وصف زوايا الميل، وخط الطول للعقدة الصاعدة، وحجة القبوة الحضيضية على أنها زوايا أويلر التي تحدد اتجاه المدار بالنسبة إلى نظام الإحداثيات المرجعية.
لاحظ أن المسارات غير الإهليلجية موجودة أيضا، ولكنها ليست مغلقة، وبالتالي فهي ليست مدارات. إذا كان الانحراف أكبر من واحد يكون المسار هذلولي. وإذا كان الانحراف يساوي واحد والزخم الزاوي صفر يكون المسار محوري[2] . وإذا كان الانحراف واحد، وهناك زخم زاوي يكون المسار شلجمي.
المعلمات المطلوبة
لتحديد إطار مرجعي قصوري معين وحقبة مختارة (نقطة محددة في الوقت المناسب)، فإن هناك ست معلمات ضرورية لتحديد وبشكل لا لبس فيه مدار مختار وغير مضطرب. وذلك لأن المسألة تحتوي على ست درجات حرية. وهذا يتوافق مع الأبعاد المكانية الثلاثة التي تحدد الموقع (x, y, z في نظام الإحداثيات الديكاَرتية) بالإضافة إلى السرعة في كل من هذه الأبعاد. ويمكن وصفها بأنها متجهات الدالة المدارية، ولكن هذة وسيلة غالبا ما تكون غير ملائمة لتمثيل المدار، وهذا هو سبب استخدام العناصر الكبلرية بدلا من ذلك.
تمثيل بديل
ويمكن الحصول على العناصر الكبلرية من متجهات الدالة المدارية (ثلاثة متجهات للموقع وثلاث للسرعة) عن طريق تحويل يدوي أو من خلال برامج الحاسوب.[3]
ويمكن حساب المعلمات المدارية الأخرى من العناصر الكبلرية مثل الفترة المدارية ، والقبا (فترتي الأوج والحضيض). ومن الشائع تحديد الفترة بدلا من نصف المحور الرئيسي في نظام العناصر الكبلرية، حيث يمكن حساب كل منها من الآخر بشرط أن يكون معامل الجاذبية القياسي ،GM، معروف للجسم المركزي.
وتستخدم مجموعات مختلفة من العناصر لمختلف الأجرام الفلكية. فعلى سبيل المثال يستخدم الانحراف، ونصف المحور الرئيسي، أو مسافة الحضيض، لتحديد شكل وحجم المدار.وتستخدم زاوية العقدة الصاعدة والميل وحجة القبوة الحضيضية، أو خط طول الحضيض، لتحديد اتجاه المدار في مستواه.ويستخدم خط الطول في حقبة ومتوسط الشذوذ في حقبة، أو وقت اجتياز الحضيض، لتحديد نقطة معروفة في المدار. وتعتمد الخيارات التي يتم اتخاذها على ما إذا كان الاعتدال الربيعي أو العقدة تستخدم كمرجع أساسي. ويحدد نصف المحور الرئيسي إذا كانت الحركة المتوسطة وكتلة الجاذبية معروفة.[4][5]
ومن الشائع أيضا حساب متوسط الشذوذ (M) أو خط الطول المتوسط (L) من دون متوسط الشذوذ في حقبةM0 أو خط طول في حقبةL0، كخطوات وسيطة بوصفها دالة متعددة الحدود فيما يتعلق بالوقت. وأسلوب التعبير هذا يدعم الحركة المتوسطة (n) في المتغيرات الحدية باعتبارها واحدة من المعاملات.
مصادر
- The Ulysses Orbit: Classical Orbital Elements - تصفح: نسخة محفوظة 09 سبتمبر 2015 على موقع واي باك مشين.
- William Tyrrell Thomson (1986), Introduction to Space Dynamics, Dover
- Keplerian Elements Resources - تصفح: نسخة محفوظة 09 سبتمبر 2017 على موقع واي باك مشين.
- Green, Robin M. (1985). Spherical Astronomy. Cambridge University Press. .
- Danby, J. M. A. (1962). Fundamentals of Celestial Mechanics. Willmann-Bell. .