قطع زائد

القطع الزائد (Hyperbola) (في اللغة الإغريقية ὑπερβολή) أو الهذلول، هو أحد أنماط القطوع المخروطية (conic sections).^[1][2]

القُطوعُ المخروطيَّةُ

هذه المقالةُ جزءٌ من سلسلةِ القطوع المخروطية
قطع مكافئ
المعادلة	${\displaystyle y^{2}=4ax\,}$
الانحراف المركزي(${\displaystyle e}$)	${\displaystyle 1\,}$
البعد البؤري(${\displaystyle l}$)	${\displaystyle 2a\,}$
قطع زائد
المعادلة	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$
الانحراف المركزي (${\displaystyle e}$)	${\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$
البعد البؤري(${\displaystyle l}$)	${\displaystyle {\frac {b^{2}}{a}}}$
قطع ناقص
المعادلة	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$
الانحراف المركزي (${\displaystyle e}$)	${\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$
البعد البؤري (${\displaystyle l}$)	${\displaystyle {\frac {b^{2}}{a}}}$
دائرة (حالة خاصة من القطع الناقص)
المعادلة	${\displaystyle x^{2}+y^{2}=a^{2}\,}$
الانحراف المركزي (${\displaystyle e}$)	${\displaystyle 0}$
البعد البؤري (${\displaystyle l}$)	${\displaystyle a}$
• ' • ' •

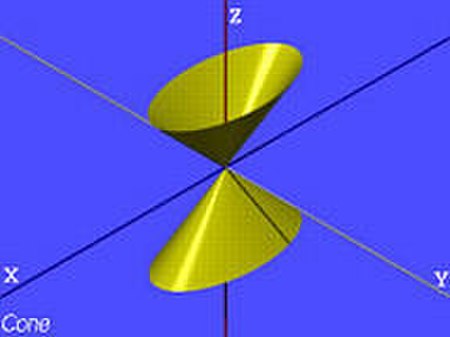
القطع الزائد ناتج عن قطع المخروط بمستو في أحد نصفي المخروط، وهو الذي يكون اختلافه المركزي أكبر من الواحد الصحيح، ويمكن تعريفه بعبارة أخرى: وهو القطع الذي ينشأ عن قطع سطح مخروطي دائري قائم وامتداده من جهة رأسه بمستو يميل على مستوى دليله بزاوية أكبر من زاوية ميل أحد الرواسم على مستوى الدليل.

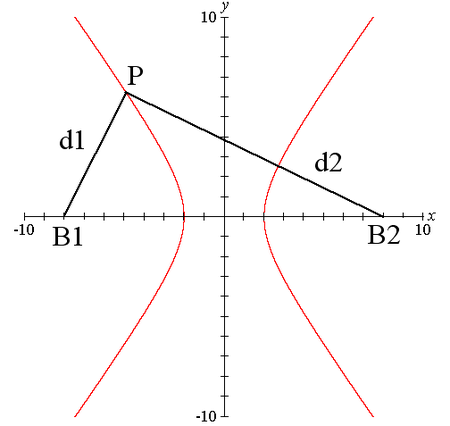
ويعرف أيضا على أنه مجموعة النقاط التي تتميز بكون فرق مسافة هذه النقاط عن نقطتين ثابتتين ( تدعى البؤرتين ) هو عدد ثابت .

ونقول أن القطعان الزائدان متشابهين (Similar)، إذا كان اختلافهما المركزيان متساويين، ويكون قطعان زائدان مترافقين إذا كان المحور المستعرض لأحدهما هو المحور المرافق للآخر والمحور المرافق للأول هو المستعرض للآخر.

المعادلة في الإحداثيات الديكارتية

المعادلة للقطع الزائد هي:
${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$ إذا هي تقطع المحور الأفقي x
و ${\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1}$ إذا هي تقطع المحور الرأسي y
حيث a هو قيمة مطلقة ل x إذا المعادلة تقطع المحور x و b قيمة مطلقة ل y إذا المعادلة تقطع المحور y
وكما في الصورة السابقة: الجزء من خط التقارب المائل هو (a, b) و${\displaystyle b={\sqrt {a^{2}+c^{2}}}}$
حيث c هو أقصر مسافة من نقطة الأصل إلى البؤرة B2
ومعادلة الخط التقاربي ${\displaystyle y=\pm x\times {\frac {a}{b}}}$ للمعادلة ${\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1}$

و${\displaystyle y=\pm x\times {\frac {b}{a}}}$ للمعادلة ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$.^[3]

في الهندسة الوصفية

قطع زائد كمحل هندسي لمراكز الدوائر الماسة دائرتين معلومتين Θ Δ

القطع الزائد في الهندسة الوصفية, يمكن الحصول عليه:

• عن طريق قطع مخروط دوراني K بمستوى موازي لاثنين من راسمين سطح K.
• كمحل هندسي لمراكز الدوائر الماسة دائرتين معلومتين Θ Δ، في الظروف التي تكون فيها تلك الدائرتين Θ Δ متقاطعتين أو خارجتين عن بعضهما البعض (اي ان لا تكون الواحدة داخل الأخرى) وان يكون مختلف نصف قطرهما. في الحالة التي يكون فيها تساوي بين الدائرتين Θ Δ, المحل الهندسي الناتج يكون مكون من نقاط تنتمي إلى خط مستقيم الذي ينطبق مع محور تماثل الدائرتين.
  • بشكل عام، يين اهليجين متشابهين ومتحدي المستوى، يتم تعريف القطع الناقص بالمحل الهندسي لمراكز الاهاليج المتشابهة للاهليجين المعلومين بحيث يكونوا متماسين لنفس الاهليجين.

عيين اهليجين متشابهين ومتحدي المستوى، يتم تعريف القطع الناقص بالمحل الهندسي لمراكز الاهاليج المتشابهة للاهليجين المعلومين بحيث يكونوا متماسين لنفس الاهليجين

معرض صور

مقالات ذات صلة

• قطع مكافيء.
• قطع ناقص.
• دالة زائدية
• قطع مخروطي
• اختلاف مركزي (رياضيات)

مراجع

موسوعات ذات صلة :

• موسوعة رياضيات
• موسوعة هندسة رياضية