مساحة القرص

في الهندسة الرياضية، مساحة القرص (Area of a disk)‏ (هي المساحة الموجودة داخل دائرة ما) تساوي π r² حيث r هو شعاع هذه الدائرة وحيث الحرف الإغريقي π هو ثابتة تساوي تقريبا 3.14159. وقيمة هذه التابتة هي نسبة محيط دائرة ما إلى قطرها.

واحدة من الطرق المؤدية إلى هذه الصيغة انبثقت من رؤية الدائرة نهايةَ متتالية لمضلعات منتظمة. يرجع الفضل في هذه الصيغة إلى العالم الإغريقي أرخميدس.

التاريخ

دُرست مسألة مساحة القرص من طرف الإغريق القدامى.

انظر إلى هلال أبقراط.

استعمال متعددي الأضلاع

مساحة مضلع منتظم تساوي نصف محيطه مضروبا في المسافة الفاصلة بين مركز المضلع وأحدٍ من أضلاعه. كلما كبُر عدد أضلاع مضلع منتظم، كلما اقترب المضلع المنتظم من الدائرة التي تضمه، وكلما اقتربت هذه المسافة من شعاع الدائرة. هذا الأمر يؤكد أن مساحة القرص تساوي نصف محيط الدائرة مضروبا في شعاعها.

برهان أرخميدس

ليس أكبر من

دائرة ومربع وثماني أضلاع. الدائرة محيطة بهما مبينة الفرق في المساحة باللون الأصفر.

انظر إلى دائرة محيطة.

${\displaystyle {\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}}$

ليس أصغر من

دائرة ومربع وثماني أضلاع. الدائرة محاطة بهما مبينة الفرق في المساحة باللون الأصفر.

${\displaystyle {\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}}$

براهين عصرية

برهان البصلة

مساحة القرص بواسطة تكامل الحلقات

انظر بصل.

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=\left[(2\pi ){\frac {t^{2}}{2}}\right]_{t=0}^{r}\\&{}=\pi r^{2}.\end{aligned}}}$

طريقة المثلث

نشرت الدائرة من أجل تكوين مثلث.

الصيغة المستعملة من أجل حساب مساحة المثلث.

${\displaystyle {\begin{aligned}Area&{}={\frac {1}{2}}*base*height\\&{}={\frac {1}{2}}*2\pi r*r\\&{}=\pi r^{2}\end{aligned}}}$

طريقة نصف الدائرة

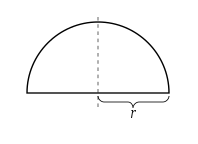
نصف دائرة شعاعها r

باستعمال تعريف التكامل ذاته، يمكن أن يُستنتج أن مساحة نصف الدائرة تساوي

${\displaystyle \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx}$

باستعمال تعويض مثلثي يتمثل في وضع ${\displaystyle x=r\sin \theta }$، نجد أن ${\displaystyle dx=r\cos \theta \,d\theta .}$

${\displaystyle =\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}{\sqrt {r^{2}(1-\sin ^{2}\theta )}}\cdot r\cos \theta \,d\theta }$

${\displaystyle =2r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta \,d\theta }$

${\displaystyle ={\frac {\pi r^{2}}{2}}.}$

تقريب سريع

الاشتقاق

التقريب بالرمي بالنبال

تحديد مساحة الدائرة باستعمال طريقة تكامل مونت كارلو. التقدير ب 900 عينة يعطي 4×⁷⁰⁹⁄₉₀₀ = 3.15111...

انظر طريقة مونت كارلو.

تعميمات

مراجع

وصلات خارجية

• مساحة القرص مع رسوم متحركة

موسوعات ذات صلة :

• موسوعة رياضيات