مغناطيسية الجاذبية

تاثير انحناء الزمكان على جيروسكوب في مدار حول الأرض. تجربة مسبار الجاذبية.

مغناطيسية الجاذبية في الفيزياء (بالإنجليزية: Gravitomagnetism) هي معادلات تماثل معادلات ماكسويل ومستنبطة منن النظرية النسبية العامة لأينشتاين تحت شروط معينة. وهي تنطبق على مشاهدة من بعيد لمصادر معزولة، وتنطبق فقط على جسيمات بطيئة. نشرت تلك المعادلات أول مرة 1893 قبل صياغة النظرية النسبية العامة قام بصياغتها الفيزيائي أولفر هيفيسايد كنظرية مستقلة مكملة لقوانين نيوتن.

^[1]

مقدمــة

يتصور هذا التقريب الجاذبية كما تصفها النظرية النسبية العامة كقوة تخيلية تظهر في إطار مرجعي مختلف عن الإطار المرجعي لجسم يتحرك ذو جاذبية. وبالتماثل مع الكهرومغناطيسية تسمى تلك القوة التخيلية قوة مغناطيسية الجاذبية حيث أنها تنشأ مثلما في حالة شحنة كهربائية متحركة فهي تنشئ مجالا مغناطيسيا. ويترتب على تلك القوة المغناطيسية الجاذبية أن جسما ساقطا حرا عل جرم كبير الكتلة يدور حول محوره أن يدور الجسم الساقط أيضا بالتأثير.

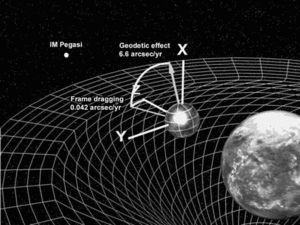
وقد استنبطت اثباتات غير مباشرة لهذا التأثير عن تحليل للنفاثات ذات سرعة الضوء المشاهدة في بعض الظواهر الفلكية مثل مجرة نشطة ووثقوب سوداء. وقد اقترح العالم الفيزيائي البريطاني روجر بنروز وسيلة تسمى تباطؤ الإطار المرجعي لاستخراج طاقة وزخم حركة من ثقب أسود يدور حول محوره. ^[2] ثم طورت الفيزيائية ريفا وليامز - الباحثة في جامعة فلوريدا - إثباتا لطريقة بنروز. ^[3] وفسرت كيف يؤدي تأثير لينز-ثيرينج إلى إنتاج تلك الطاقة والضياء الفائقين المشاهدة في النجوم الزائفة وفي حوصلة مجرةمجرة نشطة ، وتلك النفاثات الضيقة التي تنطلق من قطبيها. ^[4] وقد أمكن تفسير جميع تلك الظواهر بواسطة تأثيرات مغناطيسية الجاذبية. ^[5] ويمكن تطبيق طريقة وليامز على عمليات بنروز بالنسبة لجميع أنواع الثقوب السوداء على احتلاف كتلتها. ^[6]

وتقوم مجموعة من الباحثين من جامعة ستانفورد بتحليل البيانات التي قام بقياسها مسبار الجاذبية Gravity Probe B للتأكد من صحة تنبؤات المغناطيسية الجاذبية. كما يزمع مرصد أباشي لقياس بُعد القمر بالليزر دراسة تأثيرات المغناطيسية الجاذبية.

المعادلات

طبقا للنظرية النسبية العامة يمكن وصف مجال الجاذبية الناتج عن دوران جسم بواسطة معادلات مشابهة لتلك المستخدمة في معادلات ماكسويل للمجال المغناطيسي في الكهرومغناطيسية. بالابتداء من المعادلة الأساسية للنسبية العامة - معادلة المجال لأينشتاين - وبافتراض مجال جاذبية ضعيف أو زمكان مستوى يمكن استنتاج معادلات الجاذبية المماثلة لمعادلات ماكسويل للكهرومغناطيسية. تسمى تلك المعادلات "معادلات مغناطيسية الجاذبية" GEM equations ونقارنها هنا بمعادلات ماكسويل بوحدات SI : ^{[7][8][9][10][11]}

معادلات مغناطيسية الجاذبية	معادلات ماكسويل
${\displaystyle \nabla \cdot \mathbf {E} _{\text{g}}=-4\pi G\rho _{\text{g}}\ }$	${\displaystyle \nabla \cdot \mathbf {E} ={\frac {\rho }{\epsilon _{0}}}}$
${\displaystyle \nabla \cdot \mathbf {B} _{\text{g}}=0\ }$	${\displaystyle \nabla \cdot \mathbf {B} =0\ }$
${\displaystyle \nabla \times \mathbf {E} _{\text{g}}=-{\frac {\partial \mathbf {B} _{\text{g}}}{\partial t}}\ }$	${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}\ }$
${\displaystyle \nabla \times \mathbf {B} _{\text{g}}=-{\frac {4\pi G}{c^{2}}}\mathbf {J} _{\text{g}}+{\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} _{\text{g}}}{\partial t}}}$	${\displaystyle \nabla \times \mathbf {B} ={\frac {1}{\epsilon _{0}c^{2}}}\mathbf {J} +{\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}}$

حيث:

• E_g مجال جاذبية ثابت، يمكن أن يسمى كهربائية الجاذبية gravitoelectric لتسهيل المقارنة
• E مجال كهربائي;
• B_g مجال مغناطيسية الجاذبية;
• B مجال مغناطيسي;
• ρ_g كثافة المادة;
• ρ كثافة الشحنة:
• J_g كثافة التيار (J = ρ v_ρ)

حيث v_ρ سرعة سريان الكتلة المنتجة لمجال مغناطيسية الجاذبية

• J كثافة التيار الكهربائي;
• G ثابت الجاذبية;
• ε₀ نفاذية الفراغ;
• c سرعة انتشار الجاذبية = سرعة الضوء طبقا للنسبية العامة.

مجال مغناطيسية الجاذبية لجرم فلكي

يمكن استنباط معادلة مجال مغناطيسية الجاذبية B_g باقرب من جرم سماوي يجور ومحوره بتطبيق معادلات مغناطيسية الجاذبية، وهي: ^[8]

${\displaystyle \mathbf {B} _{\text{g}}={\frac {G}{2c^{2}}}{\frac {\mathbf {L} -3(\mathbf {L} \cdot \mathbf {r} /r)\mathbf {r} /r}{r^{3}}},}$

حيث:

• L زخم الدوران للجرم.

وعلى مستوي الخط الاستوائي للدوران تكون r وL متعامدتين، وبذلك يختفي حاصل ضربهما ببعض dot product.

وتختصر المعادلة بالشكل:

${\displaystyle \mathbf {B} _{\text{g}}={\frac {G}{2c^{2}}}{\frac {\mathbf {L} }{r^{3}}},}$

وهذه القيمة لعزم الدوران هي لجسم كروي متساوي الكثافة.

${\displaystyle L=I_{\text{ball}}\omega ={\frac {2mr^{2}}{5}}{\frac {2\pi }{T}}}$

حيث:

• ${\displaystyle I_{\text{ball}}={\frac {2mr^{2}}{5}}}$ عزم القصور الذاتي للجسم الكروي (انظر قائمة عزم القصور الذاتي);
• ${\displaystyle \omega \ }$ سرعة زاوية;
• m الكتلة;
• r نصف القطر;
• T الدورة (زمن دورة واحدة).

معداة مجال مغناطيسية الجاذبية للأرض

بناء على ما ذكرناه أعلاه يمكننا حساب مجال مغناطيسية الجاذبية للأرض عند خط الإستواء:

${\displaystyle B_{\text{g, Earth}}={\frac {G}{5c^{2}}}{\frac {m}{r}}{\frac {2\pi }{T}}={\frac {2\pi rg}{5c^{2}T}},}$

حيث ${\displaystyle g=G{\frac {m}{r^{2}}}}$ جاذبية الأرض.

ينطبق اتجاه قوة امغناطيسية الجاذبية للأرض على اتجاه عزم دورانها أي نحو الشمال.

ينتج عن ذلك أن مجال مغناطيسية الجاذبية لكوكب الأرض عند خط الاستواء يبلغ B_{g, Earth} = 1.012×10⁻¹⁴ هرتز,^[12]

أو: 3.1×10⁻⁷ بوحدات عجلة الجاذبية (9.81 m/s²) مقسومة على سرعة الضوء.

هذه قيمة صغيرة جدا ويتطلت قياسها أجهزة حساسة جدا. وقد جهزت تجربة دقيقة جدا على متن قمر صناعي يدور حول الأرض (مسبار الجاذبية) أطلقته ناسا عام 2004 لقياسة.

المراجع

مقالات ذات صلة

• تباطؤ الإطار المرجعي
• مسبار الجاذبية
• تسارع زاوي
• عزم زاوي
• بدارية
• بدارية لارمور
• عزم الدوران
• عزم القصور الذاتي
• جيروسكوب
• الجاذبية

موسوعات ذات صلة :

• موسوعة علم الفلك
• موسوعة الفيزياء