Loi uniforme discrète

Loi discrète uniforme sur l'ensemble $\{1,2,\cdots ,n\}$

Fonction de masse ${\text{ ci-dessus et ci-dessous, }}n=6$
Fonction de répartition

Paramètres	$n,{\text{ entier naturel}}\neq 0$
Support	$\{1,2,\cdots ,n\}$
Fonction de masse	${\begin{cases}{\frac {1}{n}}&{\text{pour }}k\in \{1,2,\cdots ,n\}\\0&{\text{sinon}}\end{cases}}$ ^[1]
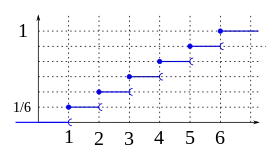
Fonction de répartition	${\begin{cases}0&{\text{pour }}k<1\\{\frac {\lfloor k\rfloor }{n}}&{\text{pour }}1\leq k<n\\1&{\text{pour }}k\geq n\end{cases}}$ ^[2]
Espérance	${\frac {n+1}{2}}$
Médiane	${\frac {n+1}{2}}$
Variance	${\frac {n^{2}-1}{12}}$
Asymétrie	$0$
Kurtosis normalisé	$-{\frac {6(n^{2}+1)}{5(n^{2}-1)}}$
Entropie	$\ln(n)$
Fonction génératrice des moments	${\begin{cases}{\frac {\mathrm {e} ^{t}}{n}}{\frac {\mathrm {e} ^{nt}-1}{\mathrm {e} ^{t}-1}}&{\text{pour }}t\neq 0\\1&{\text{pour }}t=0\end{cases}}$
Fonction caractéristique	${\begin{cases}{\frac {\mathrm {e} ^{\mathrm {i} t}}{n}}{\frac {\mathrm {e} ^{\mathrm {i} nt}-1}{\mathrm {e} ^{\mathrm {i} t}-1}}&{\text{pour }}t\neq 0\\1&{\text{pour }}t=0\end{cases}}$

En théorie des probabilités, une loi discrète uniforme est une loi de probabilité discrète pour laquelle la probabilité de réalisation est identique (équiprobabilité) pour chaque modalité d’un ensemble fini de modalités possibles.

C'est le cas par exemple de la loi de la variable aléatoire donnant le résultat du lancer d'une pièce équilibrée, avec deux modalités équiprobables : Pile, et Face. C'est aussi le cas de celle donnant le résultat du jet d'un dé équilibré.

Cas général

Présentation

Une variable aléatoire $X$ suit une loi discrète uniforme si $X$ peut prendre $n$ modalités distinctes $k_{1},k_{2},\cdots ,k_{n},$ avec la probabilité ${\tfrac {1}{n}}$ pour chaque modalité $k_{i}.$

Plus formellement :

Le support d'une variable aléatoire $X$ est l'ensemble $\mathrm {A}$ de toutes les modalités distinctes que $X$ peut prendre.

$X$ est dite discrète, et uniforme sur $\mathrm {A} ,$ si le cardinal $\#\mathrm {A}$ de $\mathrm {A}$ est fini, et si $X$ prend ses modalités avec équiprobabilité.

Calcul d'une probabilité

La loi uniforme sur un ensemble $\mathrm {A}$ se note parfois $\mathbb {U} _{\mathrm {A} }.$ Soient $\mathrm {A}$ un ensemble fini et $X$ une variable aléatoire suivant ${\displaystyle \mathbb {U} _{\mathrm {A} }\$ on note :

\mathbb {P} (X=k)=\mathbb {U} _{\mathrm {A} }(\{k\})={\frac {1\!\!1_{\mathrm {A} }(k)}{\#\mathrm {A} }},

où $1\!\!1_{\mathrm {A} }$ désigne la fonction indicatrice (ou caractéristique) de l'ensemble $\mathrm {A} .$ D'un point de vue pratique,

\mathbb {P} (X\in B)=\sum _{k\in B}\mathbb {P} (X=k)=\sum _{k\in B}{\frac {1\!\!1_{\mathrm {A} }(k)}{\#\mathrm {A} }}={\frac {\#(\mathrm {A} \cap B)}{\#\mathrm {A} }}.

Cas particuliers

Modalités qualitatives

Un exemple simple de loi discrète uniforme à modalités qualitatives est le lancer d’une pièce de monnaie équilibrée. L'ensemble des $n=2$ modalités possibles de $X$ est $A = {Pile, Face$ } ; et à chaque fois que la pièce est lancée, la probabilité d’un résultat donné vaut ${\tfrac {1}{2}}.$

Un autre exemple est la loi donnant la couleur d'une carte tirée au hasard dans un jeu de 32 cartes indiscernables (sauf leurs faces). L'ensemble des $n=4$ couleurs possibles de $X$ est $A = {Pique, Cœur, Carreau, Trèfle$ } ; et à chaque fois qu'une carte est tirée (avec remise), la probabilité d’un résultat donné vaut ${\tfrac {1}{4}}.$

Considérons l'événement « La couleur de la carte n'est pas Pique » :

(X\neq {\text{Pique}})\Leftrightarrow (X\in B),

où

B = {Cœur, Carreau, Trèfle

}. Attention : en toute rigueur,

B

n'est pas un événement de l'univers

\Omega

des 32 cartes, mais de l'univers image de

\Omega

par

X:

celui des quatre couleurs possibles. Le cardinal de

B

est

3

(et non pas 24), donc en appliquant la dernière formule du § Calcul d'une probabilité,

\mathbb {P} (X\in B)={\tfrac {\#B}{\#\mathrm {A} }}={\tfrac {3}{4}}.

Modalités quantitatives

Valeurs entières consécutives

Un exemple simple de loi discrète uniforme à valeurs entières consécutives est le jet d’un dé non biaisé. L'ensemble des $n=6$ valeurs possibles de $X$ est ${\displaystyle \mathrm {A} =\{1,2,3,4,5,6\}\$ et à chaque fois que le dé est jeté, la probabilité d’un résultat donné vaut ${\tfrac {1}{6}}.$

Le tableau ci-contre concerne la loi discrète uniforme sur l'ensemble $\{1,2,\cdots ,n\}.$ Elle n'est qu'un cas particulier de loi discrète uniforme, mais elle est importante car elle génère l'ensemble des autres cas : si $Y$ suit une loi discrète uniforme sur $\mathrm {A} =\{k_{1},k_{2},\cdots ,k_{n}\},$ alors il existe une fonction $\psi$ telle que $Y=\psi (X),$ où $X$ est une variable aléatoire suivant la loi discrète uniforme sur l'ensemble $\{1,2,\cdots ,n\}.$ De plus, si $Y$ est quantitative, alors on peut prendre pour $\psi$ une fonction réelle infiniment dérivable^[3].

L'espérance d'une variable aléatoire $X$ suivant la loi $\mathbb {U} _{\{1,2,\cdots ,n\}}$ est^[4]:

\mathbb {E} (X)={\frac {n+1}{2}}.

Sa variance est^[4]:

\mathbb {V} (X)={\frac {n^{2}-1}{12}}.

Sa fonction génératrice des moments est^[5]:

\mathrm {M} _{X}(t)=\mathbb {E} \left(\mathrm {e} ^{tX}\right)={\frac {1}{n}}\sum _{k=1}^{n}\mathrm {e} ^{tk}={\frac {\mathrm {e} ^{t}}{n}}{\frac {\mathrm {e} ^{tn}-1}{\mathrm {e} ^{t}-1}}\quad \forall t\neq 0,\quad

\ \mathrm {M} _{X}(0)=1.

Sa fonction caractéristique est^[6]:

\Phi _{X}(t)=\mathbb {E} \left(\mathrm {e} ^{\mathrm {i} tX}\right)={\frac {1}{n}}\sum _{k=1}^{n}\mathrm {e} ^{\mathrm {i} tk}={\frac {\mathrm {e} ^{\mathrm {i} t}}{n}}{\frac {\mathrm {e} ^{\mathrm {i} tn}-1}{\mathrm {e} ^{\mathrm {i} t}-1}}\quad \forall t\neq 0,\quad

\ \Phi _{X}(0)=1.

On peut généraliser ces résultats, par translation de valeur algébrique $a-1,$ à une loi uniforme sur $n$ entiers consécutifs :

{\begin{matrix}\mathrm {A} &=&\{k_{1},&k_{2},&\cdots ,&k_{n-1},&k_{n}\}\\&=&\{a,&a+1,&\cdots ,&b-1,&b\}&=&[\![a,b]\!],\end{matrix}}

où $n=b-a+1.$

Son espérance est :

\mathbb {E} (X)=a-1+{\frac {n+1}{2}}={\frac {a+b}{2}}.

Sa variance (invariante par translation) est :

\mathbb {V} (X)={\frac {n^{2}-1}{12}}.

Valeurs réelles ou entières

Si les modalités d’une variable aléatoire uniforme discrète $X$ sont des nombres (entiers ou réels), c.-à-d. si $\mathrm {A} =\{k_{1},k_{2},\cdots ,k_{n}\}$ est une partie (finie) de $\mathbb {Z}$ ou $\mathbb {R} ,$ alors on peut exprimer probabilité, espérance, et fonction de répartition (c.-à-d. distribution cumulative) en termes de distribution·s déterministe·s.

Soit $(\Omega ,{\mathcal {T}},\mathbb {P} )$ un espace probabilisé.

Probabilité

En utilisant des notations de la théorie de la mesure, on peut exprimer la probabilité $\mathbb {P} _{X}$ par :

\mathbb {P} _{X}=\mathbb {U} _{\mathrm {A} }={\frac {1}{n}}\sum _{i=1}^{n}\delta _{k_{i}};

c.-à-d. :

\forall B\in {\mathcal {B}}(\mathbb {R} ),\quad \mathbb {P} (X\in B)=\mathbb {U} _{\mathrm {A} }(B)={\frac {1}{n}}\sum _{i=1}^{n}\delta _{k_{i}}(B),

où

\delta _{x_{0}}

désigne la mesure de Dirac centrée en

x_{0}.

On peut exprimer la fonction de masse $\mathrm {p} _{X}:\mathbb {R} \rightarrow [0,1]$ par :

\forall k\in \mathbb {R} ,\quad \mathrm {p} _{X}(k)=\mathbb {P} (X=k)=\mathbb {U} _{\mathrm {A} }(\{k\})={\frac {1}{n}}\sum _{i=1}^{n}\delta _{k_{i}}(\{k\}).\quad {\big (}\{k\}\in {\mathcal {B}}(\mathbb {R} ){\big )}

Fonction de répartition

On peut définir la fonction de répartition $\mathrm {F} _{X}:\mathbb {R} \rightarrow [0,1]$ par :

\forall k\in \mathbb {R} ,\quad \mathrm {F} _{X}(k)=\mathbb {P} (X\leq k).

La fonction de répartition est croissante sur $\mathbb {R} .$

La fonction de répartition peut s'exprimer par :

\forall k\in \mathbb {R} ,\quad \mathrm {F} _{X}(k)={1 \over n}\sum _{i=1}^{n}\mathrm {H} (k-k_{i}),

où $\mathrm {H} (x-x_{0})$ désigne la fonction marche de Heaviside translatée de $x_{0},$ c.-à-d. la fonction de répartition correspondant à la distribution déterministe centrée en ${\displaystyle x_{0}\$ cette distribution est aussi appelée masse de Dirac en $x_{0}.$ Cela suppose d'adopter la convention $\mathrm {H} (0)=1.$

Espérance

L'espérance d'une loi uniforme discrète de support $\mathrm {A} =\{k_{1},k_{2},\cdots ,k_{n}\},$ partie (finie) de $\mathbb {R}$ ou $\mathbb {Z} ,$ est :

{\displaystyle \mathbb {E} (X)={\frac {1}{n}}\sum _{i=1}^{n}k_{i}\

c.-à-d., plus simplement^[7]:

\mathbb {E} (X)={\frac {k_{1}+k_{2}+\cdots +k_{n}}{n}}.

De façon plus générale, si $X$ est une variable aléatoire suivant une loi uniforme discrète de support un ensemble $\mathrm {A} =\{k_{1},k_{2},\cdots ,k_{n}\}$ (fini) quelconque, et si $\varphi$ est une fonction définie sur $\mathrm {A}$ et à valeurs réelles, alors, par théorème de transfert^[8]:

\mathbb {E} {\big (}\varphi (X){\big )}={\frac {1}{n}}\sum _{i=1}^{n}\varphi (k_{i}).

Somme

La somme

S

des résultats de deux dés identiques (indépendants) suit une loi discrète non uniforme.

La somme de deux variables aléatoires, même indépendantes, suivant des lois discrètes uniformes de même étendue suit une loi discrète non uniforme^[9].

Par exemple, sur la figure triangulaire,

\mathbb {P} (S=2)={\tfrac {1}{36}}\neq \mathbb {P} (S=3)={\tfrac {2}{36}}={\tfrac {1}{18}}.

La somme de deux variables aléatoires indépendantes suivant des lois discrètes uniformes d'étendues différentes peut suivre une loi discrète uniforme.

Par exemple, la somme des résultats d'un dé à dix faces numérotées en dizaines (00, 10, 20, ···, 90) et d'un dé à dix faces numérotées en unités (de 0 à 9) suit la loi discrète uniforme de support

\{00,01,02,\cdots ,98,99\}.

Simulation

Il est possible de simuler une loi uniforme discrète sur $\{1,2,\cdots ,n\}$ à l'aide de la loi uniforme continue sur $[0,1[,$ en faisant l'observation suivante^[10]: si $U$ suit la loi $\mathbb {U} _{[0,1[}$ et si $X$ est définie par $X=\lfloor nU\rfloor +1,$ où $\lfloor \cdot \rfloor$ est la fonction partie entière, alors $X$ suit la loi $\mathbb {U} _{\{1,2,\cdots ,n\}}.$

Notes et références

↑ Dans Fonction de masse (probabilités)#Fonction de masse d'une loi de probabilité [non associée à une variable aléatoire], la fonction de masse est définie seulement sur $\Omega$ (qui peut être discret, et même fini).
↑ Ici, $\lfloor k\rfloor$ représente la partie entière de $k.$
↑ « Fondements du calcul mathématique des probabilités » [PDF] (consulté le 9 mars 2023), p. 3 (19.2)
1 2 Michel Lejeune, Statistique : la théorie et ses applications, Springer Science et Business Media, 2004, p. 45, 46
↑ Francesco Caravenna, Paolo Dai Pra et Quentin Berger, Introduction aux probabilités : Modèles et applications : mathématiques, physique, informatique, sciences de l'ingénieur, biologie, Dunod, 1^er septembre 2021, p. 156
↑ Ledoux, « Leçon 10. Description d'une loi de probabilité » [PDF], sur Université de Toulouse, 2021 (consulté le 9 mars 2023), p. 9
↑ « Loi uniforme discrète », sur Bib@math.net
↑ Rémi Moreau, « Leçon 264 : Variables aléatoires discrètes. Exemples et applications », sur ENS-Rennes (consulté le 9 mars 2023), p. 5
↑ « Loi uniforme discrète », sur Supagro.fr
↑ Quentin Berger et Shen Lin, « Introduction aux probabilités » [PDF], sur Sorbonne université, 2021/2022 (consulté le 9 mars 2023), p. 79

Voir aussi

Lien externe

(en) Eric W. Weisstein, « Discrete Uniform Distribution », sur MathWorld